Download Polygons - mathmastermindgeometry

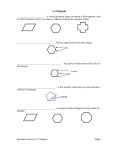
Polygon
A polygon is a two dimensional closed figure formed by three or more points joined by line
segments. These line segments intersect only at their endpoints. The word polygon comes from
Greek and means “many angles.” Simply put a polygon is a geometric figure with at least 3 sides.
The most familiar polygons are the triangle, the rectangle, and the square.
The line segments represent the sides of the polygon, and the points at which they
intersect are the vertices. A polygon has the same number of sides as it has vertices. The angles
of a polygon are the interior angles between adjacent sides. If two sides have a common endpoint,
they are said to be consecutive. The endpoints of one side are consecutive vertices. If a segment
joins two non consecutive vertices, it is called a diagonal of the polygon.
Polygons get their names from the number of sides that they have. For example a threesided polygon is a triangle, a four-sided polygon is a quadrilateral, a five-sided polygon is a
pentagon, etc. A polygon with n sides is called an n-gon.
If all the sides and all the angles of a polygon are equal the polygon is said to be regular. A
regular polygon is equilateral and equiangular. Irregular polygons have sides of differing lengths
and angles of differing measure. Unless all the sides of the polygon are of the same length and all
the angles are of the same measure the polygon is said to be irregular. Keep in mind that the names
hexagon, nonagon, pentagon and all the others do not just apply to the regular polygons but to any
two dimensional closed figure with the number of sides as described by its name.
A polygon can specifically be labeled by placing a capital letter on each vertex, moving
consecutively around the figure in either a clockwise or counterclockwise direction. This helps to
distinguish between two similar polygons. If two pentagons were placed next to each other telling
the difference between them would be difficult because they share similar characteristics. With a
label they could easily be told apart.
Why learn about polygons? Because polygons are all around us, they can be found all over
the world. They are found in numerous manufactured articles and throughout architecture. When
applied to manufactured articles such as printed fabrics, wallpapers, and tile flooring, polygons
enhance the beauty of the structure itself. Within architecture they provide a great deal of
variation and charm in buildings.
The use of polygons cannot only be said for contemporary architecture, evidence of their
use can be found throughout history, even as far back as the ancient Egypt. The Egyptians used
the idea of triangles to help create their pyramids. A pyramid is a type of polyhedron. Four of the
five faces of the Egyptians pyramid are triangles with the fifth face, or base being a square.
Glossary | Names of Polygons | Architecture | Sides & Vertices | Polyhedrons
Top of The Polygon Basics | Polygon Pop Quiz | Project Polygon Website
Polygon
Term
angle
Definition
Two rays with a common endpoint
equilateral
equiangular
irregular polygon
line segment
regular polygon
polygon
polyhedron
vertices
Having all sides equal.
Having all angles equal.
A polygon whose sides have differing lengths and angles
are of differing measure
A line that has two endpoint and does not extend beyond
these endpoints
A polygon with all sides and all angles are equal or
congruent
A closed plane figure made up of several line segments
that are joined together.
A three dimensional figure whose faces are polygons
Corners where two sides meet. (singular form is vertex)
Now you think you know it all about polygons now, test your knowledge
with this Pop Polygon Quiz. Fill out the quiz and submit it, your
results will be recorded and returned to you later.
Return to Main Page
Polygon
Regular Polygons
All the sides and angles of polygon are equal.
Triangle
Quadrilateral
Pentagon
Hexagon
Three-sided
Four-sided
Five-sided
Six-sided
Heptagon
Octagon
Nonagon
Decagon
Seven-sided
Eight-sided
Nine-sided
Ten-sided
Irregular Polygons
The measure of each side and angle of polygon differ from one another
Triangle
Quadrilateral
Pentagon
Hexagon
Three-sided
Four-sided
Five-sided
Six-sided
Heptagon
Octagon
Nonagon
Decagon
Seven-sided
Eight-sided
Nine-sided
Ten-sided
What to do now?
Try naming these | See the relationship of a polygons sides & vertices
| Return to Main Page |
Polygon
Polygons are evident throughout architecture.
Return to Main Page
Polygon
Can you identify these polygons?
2
3
1
4
5
6
1. ______________________________
2. ______________________________
3. ______________________________
4. ______________________________
5. ______________________________
6. ______________________________
Return to Main Page
Polygon
Bar Graph- Polygons vs. Sides/Vertices
Polygons: Sides & Vertices
11
10
9
7
6
5
4
3
2
1
n
ag
o
D
ec
N
o
na
g
on
on
ct
ag
O
H
ep
ta
g
on
n
ag
o
H
ex
on
ta
g
P
en
Q
ua
d
ri
a
ila
te
ng
ra
l
le
0
T
Number of
8
Type of Polygon
Return to Main Page
Sides
Vertices
Polygon
Polyhedrons
Polyhedrons are…
A three dimensional object bounded by
polygons, with each edge shared by exactly two
polygons. Various authors differ on the fine
points of the definition, e.g., whether it is a
solid or just the surface, whether it can be
infinite, and whether it can have two different
vertices that happen to be at the same location.
Polyhedron Nets
A drawing of a polyhedron unfolded along its edges to lay flat in a plane.
Platonic Solids
The Platonic solids, also called the regular solids or regular polyhedra, are
convex polyhedra with equivalent faces composed of congruent convex
regular polygons. There are exactly five such solids: the cube,
dodecahedron, icosahedron, octahedron, and tetrahedron. The Platonic solids
are sometimes also called "cosmic figures."
The Platonic solids were known to the ancient
Greeks, and were described by Plato in his Times
ca. 350 BC. In this work, Plato equated the
tetrahedron with the "element" fire, the cube
with earth, the icosahedron with water, the
octahedron with air, and the dodecahedron with
the stuff of which the constellations and
heavens were made.
Return to Main Page