* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture Slides (PowerPoint)
Survey
Document related concepts
Transcript
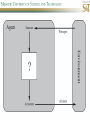
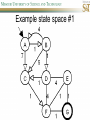
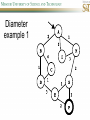
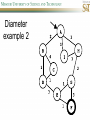
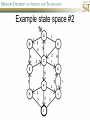
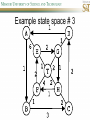
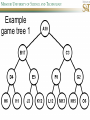
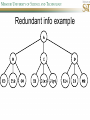
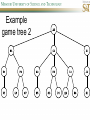
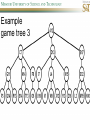
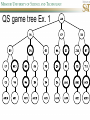
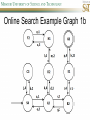
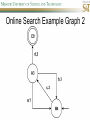
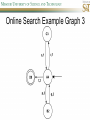
COMP SCI 5400 – Introduction to Artificial Intelligence general course website: http://web.mst.edu/~tauritzd/courses/intro_AI.html Dr. Daniel Tauritz (Dr. T) Department of Computer Science [email protected] http://web.mst.edu/~tauritzd/ What is AI? Systems that… –act like humans (Turing Test) –think like humans –think rationally –act rationally Play Ultimatum Game Computer Agent • Perceives environment • Operates autonomously • Persists over prolonged periods Rational Agents • Environment • Sensors (percepts) • Actuators (actions) Rational Agents • • • • • Environment Sensors (percepts) Actuators (actions) Agent Function Agent Program Rational Behavior Depends on: • Agent’s performance measure • Agent’s prior knowledge • Possible percepts and actions • Agent’s percept sequence Rational Agent Definition “For each possible percept sequence, a rational agent selects an action that is expected to maximize its performance measure, given the evidence provided by the percept sequence and any prior knowledge the agent has.” PEAS description & properties: –Fully/Partially Observable –Deterministic, Stochastic, Strategic –Episodic, Sequential –Static, Dynamic, Semi-dynamic –Discrete, Continuous –Single agent, Multiagent –Competitive, Cooperative –Known, Unknown Agent Types • • • • • Simple Reflex Agents Model-Based Reflex Agents Goal-Based Agents Utility-Based Agents Learning Agents Problem-solving agents A definition: Problem-solving agents are goal based agents that decide what to do based on an action sequence leading to a goal state. Environment Assumptions • • • • • Fully Observable Single Agent Discrete Sequential Known & Deterministic Open-loop problem-solving steps • Problem-formulation (actions & states) • Goal-formulation (states) • Search (action sequences) • Execute solution Well-defined problems • • • • • • • Initial state Action set: ACTIONS(s) Transition model: RESULT(s,a) Goal test Step cost: c(s,a,s’) Path cost Solution / optimal solution Example problems • • • • Vacuum world Tic-tac-toe 8-puzzle 8-queens problem Search trees • Root corresponds with initial state • Vacuum state space vs. search tree • Search algorithms iterate through goal testing and expanding a state until goal found • Order of state expansion is critical! function TREE-SEARCH(problem) returns solution/fail initialize frontier using initial problem state loop do if empty(frontier) then return fail choose leaf node and remove it from frontier if chosen node contains goal state then return corresponding solution expand chosen node and add resulting nodes to frontier Redundant paths • Loopy paths • Repeated states • Redundant paths function GRAPH-SEARCH(problem) returns solution/fail initialize frontier using initial problem state initialize explored set to be empty loop do if empty(frontier) then return fail choose leaf node and remove it from frontier if chosen node contains goal state then return corresponding solution add chosen node to explored set expand chosen node and add resulting nodes to frontier only if not yet in frontier or explored set Search node datastructure • • • • n.STATE n.PARENT-NODE n.ACTION n.PATH-COST States are NOT search nodes! function CHILD-NODE(problem,parent,action) returns a node return a node with: STATE = problem.RESULT(parent.STATE,action) PARENT = parent ACTION = action PATH-COST = parent.PATH-COST + problem.STEP-COST(parent.STATE,action) Frontier • Frontier = Set of leaf nodes • Implemented as a queue with ops: – EMPTY?(queue) – POP(queue) – INSERT(element,queue) • Queue types: FIFO, LIFO (stack), and priority queue Explored Set • Explored Set = Set of expanded nodes • Implemented typically as a hash table for constant time insertion & lookup Problem-solving performance • • • • Completeness Optimality Time complexity Space complexity Complexity in AI • • • • • • • b – branching factor d – depth of shallowest goal node m – max path length in state space Time complexity: # generated nodes Space complexity: max # nodes stored Search cost: time + space complexity Total cost: search + path cost Tree Search • • • • • Breadth First Tree Search (BFTS) Uniform Cost Tree Search (UCTS) Depth-First Tree Search (DFTS) Depth-Limited Tree Search (DLTS) Iterative-Deepening Depth-First Tree Search (ID-DFTS) Example state space #1 Breadth First Tree Search (BFTS) • Frontier: FIFO queue • Complete: if b and d are finite • Optimal: if path-cost is non-decreasing function of depth • Time complexity: O(b^d) • Space complexity: O(b^d) Uniform Cost Search (UCS) • g(n) = lowest path-cost from start node to node n • Frontier: priority queue ordered by g(n) Depth First Tree Search (DFTS) • Frontier: LIFO queue (a.k.a. stack) • Complete: no (DGFS is complete for finite state spaces) • Optimal: no • Time complexity: O(bm) • Space complexity: O(bm) • Backtracking version of DFTS: – space complexity: O(m) – modifies rather than copies state description Depth-Limited Tree Search (DLTS) • • • • • • Frontier: LIFO queue (a.k.a. stack) Complete: not when l < d Optimal: no Time complexity: O(bl) Space complexity: O(bl) Diameter: min # steps to get from any state to any other state Diameter example 1 Diameter example 2 Iterative-Deepening Depth-First Tree Search (ID-DFTS) function ID-DFS(problem) returns solution/fail for depth = 0 to ∞ do result ← DLS(problem,depth) if result ≠ cutoff then return result • Complete: Yes, if b is finite • Optimal: Yes, if path-cost is nondecreasing function of depth • Time complexity: O(b^d) • Space complexity: O(bd) Bidirectional Search BiBFTS • Complete: Yes, if b is finite • Optimal: Not “out of the box” • Time & Space complexity: O(bd/2) Example state space #2 Best First Search (BeFS) • Select node to expand based on evaluation function f(n) • Node with lowest f(n) selected as f(n) correlated with path-cost • Represent frontier with priority queue sorted in ascending order of f-values Path-cost functions • g(n) = lowest path-cost from start node to node n • h(n) = estimated non-negative path-cost of cheapest path from node n to a goal node [with h(goal)=0] Heuristics • h(n) is a heuristic function • Heuristics incorporate problemspecific knowledge • Heuristics need to be relatively efficient to compute Important BeFS algorithms • UCS: f(n) = g(n) • GBeFS: f(n) = h(n) • A*S: f(n) = g(n)+h(n) GBeFTS • Incomplete (so also not optimal) • Worst-case time and space complexity: O(bm) • Actual complexity depends on accuracy of h(n) A*S • f(n) = g(n) + h(n) • f(n): estimated cost of optimal solution through node n • if h(n) satisfies certain conditions, A*S is complete & optimal Example state space # 3 Admissible heuristics • h(n) admissible if: Example: straight line distance A*TS optimal if h(n) admissible Consistent heuristics • h(n) consistent if: Consistency implies admissibility A*GS optimal if h(n) consistent A* search notes • • • • • Optimally efficient for consistent heuristics Run-time is a function of the heuristic error Suboptimal variants Not strictly admissible heuristics A* Graph Search not scalable due to memory requirements Memory-bounded heuristic search • • • • • • Iterative Deepening A* (IDA*) Recursive Best-First Search (RBFS) IDA* and RBFS don’t use all avail. memory Memory-bounded A* (MA*) Simplified MA* (SMA*) Meta-level learning aims to minimize total problem solving cost Heuristic Functions • • • • Effective branching factor Domination Composite heuristics Generating admissible heuristics from relaxed problems Sample relaxed problem • n-puzzle legal actions: Move from A to B if horizontally or vertically adjacent and B is blank Relaxed problems: (a)Move from A to B if adjacent (b)Move from A to B if B is blank (c) Move from A to B Generating admissible heuristics The cost of an optimal solution to a relaxed problem is an admissible heuristic for the original problem. Adversarial Search Environments characterized by: • Competitive multi-agent • Turn-taking Simplest type: Discrete, deterministic, two-player, zero-sum games of perfect information Search problem formulation • • • • • • S0: Initial state (initial board setup) Player(s): which player has the move Actions(s): set of legal moves Result(s,a): defines transitional model Terminal test: game over! Utility function: associates playerdependent values with terminal states Minimax • Time complexity: O(bm) • Space complexity: O(bm) Example game tree 1 Depth-Limited Minimax • State Evaluation Heuristic estimates Minimax value of a node • Note that the Minimax value of a node is always calculated for the Max player, even when the Min player is at move in that node! Heuristic Depth-Limited Minimax State Eval Heuristic Qualities A good State Eval Heuristic should: (1)order the terminal states in the same way as the utility function (2)be relatively quick to compute (3)strongly correlate nonterminal states with chance of winning Weighted Linear State Eval Heuristic EVAL(s) i 1 wifi(s) n Heuristic Iterative-Deepening Minimax • IDM(s,d) calls DLM(s,1), DLM(s,2), …, DLM(s,d) • Advantages: –Solution availability when time is critical –Guiding information for deeper searches Redundant info example Alpha-Beta Pruning • α: worst value that Max will accept at this point of the search tree • β: worst value that Min will accept at this point of the search tree • Fail-low: encountered value <= α • Fail-high: encountered value >= β • Prune if fail-low for Min-player • Prune if fail-high for Max-player DLM w/ Alpha-Beta Pruning Time Complexity • Worst-case: O(bd) • Best-case: O(bd/2) [Knuth & Moore, 1975] • Average-case: O(b3d/4) Example game tree 2 Move Ordering Heuristics • Knowledge based (e.g., try captures first in chess) • Principal Variant (PV) based • Killer Move: the last move at a given depth that caused αβ-pruning or had best minimax value • History Table: track how often a particular move at any depth caused αβpruning or had best minimax value History Table (HT) • Option 1: generate set of legal moves and use HT value as f-value • Option 2: keep moves with HT values in a sorted array and for a given state traverse the array to find the legal move with the highest HT value Example game tree 3 Search Depth Heuristics • Time based / State based • Horizon Effect: the phenomenon of deciding on a non-optimal principal variant because an ultimately unavoidable damaging move seems to be avoided by blocking it till passed the search depth • Singular Extensions / Quiescence Search Time Per Move • • • • Constant Percentage of remaining time State dependent Hybrid Quiescence Search • When search depth reached, compute quiescence state evaluation heuristic • If state quiescent, then proceed as usual; otherwise increase search depth if quiescence search depth not yet reached • Call format: QSDLM(root,depth,QSdepth), QSABDLM(root,depth,QSdepth,α,β), etc. QS game tree Ex. 1 QS game tree Ex. 2 Transposition Tables (1) • Hash table of previously calculated state evaluation heuristic values • Speedup is particularly huge for iterative deepening search algorithms! • Good for chess because often repeated states in same search Transposition Tables (2) • Datastructure: Hash table indexed by position • Element: –State evaluation heuristic value –Search depth of stored value –Hash key of position (to eliminate collisions) –(optional) Best move from position Transposition Tables (3) • Zobrist hash key – Generate 3d-array of random 64-bit numbers (piece type, location and color) – Start with a 64-bit hash key initialized to 0 – Loop through current position, XOR’ing hash key with Zobrist value of each piece found (note: once a key has been found, use an incremental approach that XOR’s the “from” location and the “to” location to move a piece) Search versus lookup • Balancing time versus memory • Opening table – Human expert knowledge – Monte Carlo analysis • End game database Forward pruning • Beam Search (n best moves) • ProbCut (forward pruning version of alpha-beta pruning) Null Move Forward Pruning • Before regular search, perform shallower depth search (typically two ply less) with the opponent at move; if beta exceeded, then prune without performing regular search • Sacrifices optimality for great speed increase Futility Pruning • If the current side to move is not in check, the current move about to be searched is not a capture and not a checking move, and the current positional score plus a certain margin (generally the score of a minor piece) would not improve alpha, then the current node is poor, and the last ply of searching can be aborted. • Extended Futility Pruning • Razoring Adversarial Search in Stochastic Environments Worst Case Time Complexity: O(bmnm) with b the average branching factor, m the deepest search depth, and n the average chance branching factor Example “chance” game tree Expectiminimax & Pruning • Interval arithmetic • Monte Carlo simulations (for dice called a rollout) State-Space Search • • • • Complete-state formulation Objective function Global optima Local optima (don’t use textbook’s definition!) • Ridges, plateaus, and shoulders • Random search and local search Steepest-Ascent Hill-Climbing • Greedy Algorithm - makes locally optimal choices Example 8 queens problem has 88≈17M states SAHC finds global optimum for 14% of instances in on average 4 steps (3 steps when stuck) SAHC w/ up to 100 consecutive sideways moves, finds global optimum for 94% of instances in on average 21 steps (64 steps when stuck) Stochastic Hill-Climbing • Chooses at random from among uphill moves • Probability of selection can vary with the steepness of the uphill move • On average slower convergence, but also less chance of premature convergence First-choice Hill-Climbing • Choose the first randomly generated uphill move • Greedy, incomplete, and suboptimal • Practical when the number of successors is large • Low chance of premature convergence as long as the move generation order is randomized Random-restart Hill-Climbing • Series of HC searches from randomly generated initial states until goal is found • Trivially complete • E[# restarts]=1/p where p is probability of a successful HC given a random initial state • For 8-queens instances with no sideways moves, p≈0.14, so it takes ≈7 iterations to find a goal for a total of ≈22 steps Simulated Annealing function SA(problem,schedule) returns solution state current←MAKE-NODE(problem.INITIAL-STATE) for t=1 to ∞ do T←schedule(t) if T=0 then return current next←RANDOM-SUCCESOR(current) ∆E←next.VALUE – current.VALUE if ∆E > 0 then current←next else current←next with probability of e∆E/T Population Based Local Search • • • • • Deterministic local beam search Stochastic local beam search Evolutionary Algorithms Particle Swarm Optimization Ant Colony Optimization Particle Swarm Optimization • PSO is a stochastic population-based optimization technique which assigns velocities to population members encoding trial solutions • PSO update rules: PSO demo: http://www.borgelt.net/psopt.html Ant Colony Optimization • Population based • Pheromone trail and stigmergetic communication • Shortest path searching • Stochastic moves ACO demo: http://www.borgelt.net/acopt.html Online Search • • • • • Offline search vs. online search Interleaving computation & action Dynamic, nondeterministic, unknown domains Exploration problems, safely explorable Agents have access to: – ACTIONS(s) – c(s,a,s’) cannot be used until RESULT(s,a) – GOAL-TEST(s) Online Search Optimality • CR – Competitive Ratio • TAPC – Total Actual Path Cost • C* - Optimal Path Cost TAPC CR C* • Best case: CR = 1 • Worst case: CR = ∞ Online Search Algorithms • Online-DFS-Agent • Online Local Search • Learning Real-Time A* (LRTA*) function ONLINE-DFS-AGENT(s’) returns action persistent: result, untried, unbacktracked, s, a if GOAL-TEST(s’) then return stop if s’ is a new state then untried[s’]←ACTIONS(s’) if s is not null then result[s,a]←s’ add s to front of unbacktracked[s’] if untried[s’] is empty then if unbacktracked[s’] is empty then return stop else a←action b so result[s’,b]=POP(unbacktracked[s’]) else a←POP(untried[s’]) s←s’ return a Online Local Search • • • • Locality in node expansions Inherently online Not useful in base form Random Walk function LRTA*-AGENT(s’) returns action persistent: result, H, s, a if GOAL-TEST(s’) then return stop if s’ is a new state then H[s’]←h(s’) if s is not null then result[s,a]←s’ H[s]←minbϵACTIONS(s)LRTA*-COST(s,b,result[s,b],H) a←bϵACTIONS to minimize LRTA*-COST(s’,b,result[s’,b],H) s←s’ return a function LRTA*-COST(s,a,s’,H) returns a cost estimate if s’ is undefined then return h(s) else return c(s,a,s’)+H[s’] Online Search Maze Problem (Fig. 4.19) Online Search Example Graph 1a Online Search Example Graph 1b Online Search Example Graph 2 Online Search Example Graph 3 Key historical events for AI • • • • 4th century BC Aristotle propositional logic 1600’s Descartes mind-body connection 1805 First programmable machine Mid 1800’s Charles Babbage’s “difference engine” & “analytical engine” • Lady Lovelace’s Objection • 1847 George Boole propositional logic • 1879 Gottlob Frege predicate logic Key historical events for AI • 1931 Kurt Godel: Incompleteness Theorem In any language expressive enough to describe natural number properties, there are undecidable (incomputable) true statements • 1943 McCulloch & Pitts: Neural Computation • 1956 Term “AI” coined • 1976 Newell & Simon’s “Physical Symbol System Hypothesis” A physical symbol system has the necessary and sufficient means for general intelligent action. Key historical events for AI • • • • • AI Winters (1974-80, 1987-93) Commercialization of AI (1980-) Rebirth of Artificial Neural Networks (1986-) Unification of Evolutionary Computation (1990s) Rise of Deep Learning (2000s) Weak AI vs. Strong AI • Mind-Body Connection René Descartes (1596-1650) Rationalism Dualism Materialism Star Trek & Souls • Chinese Room • Ethics How difficult is it to achieve AI? • Three Sisters Puzzle • • • • • • • • • • • • • • • • AI courses at S&T CS5400 Introduction to Artificial Intelligence (FS2016,SP2017) CS5401 Evolutionary Computing (FS2016,FS2017) CS5402 Data Mining & Machine Learning (FS2016,SS2017) CS5403 Intro to Robotics (FS2015) CS5404 Intro to Computer Vision (FS2016) CS6001 Machine Learning in Computer Vision (SP2016,SP2017) CS6400 Advanced Topics in AI (SP2013) CS6401 Advanced Evolutionary Computing (SP2016) CS6402 Advanced Topics in Data Mining (SP2017) CS6403 Advanced Topics in Robotics CS6405 Clustering Algorithms CpE 5310 Computational Intelligence CpE 5460 Machine Vision EngMgt 5413 Introduction to Intelligent Systems SysEng 5212 Introduction to Neural Networks and Applications SysEng 6213 Advanced Neural Networks