Download Testing for the Mean of a Population

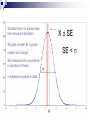
Inferring the Mean and
Standard Deviation of a
Population
Central Problem

Two important numbers tell us a lot about
a distribution of data:
Mean tells us the central tendency of the data
 Standard deviation tells us the spread in the data


The problem is … we don’t normally know
either of these and must infer them from a
SRS of the population
Baby Paradox
Two hospitals in the same city
deliver, on average, a 50:50 ratio
of baby girls and baby boys.
Hospital A delivers 120 babies a
day (on average) while hospital B
delivers 12 babies a day (on
average). One day there were
twice as many boys as girls born in
one of the hospitals. In which
hospital is this more likely to
happen?
Measuring the mean…
How do we know the mean of a
population?
 Answer: We can either measure every
single sample in the population or estimate
the mean from a suitable SRS

 We
will assume that the population is normally
distributed so X has a normal distribution
N(m,s/√n)
Standard Error and Standard
Deviation

These are two very distinct and different ideas:
 Standard
error measures the uncertainty in the
measure of the mean

This depends on how YOU measure and sample size
 Standard


deviation measures the spread in the data
This is a property of the data set – does not change
We can often estimate the standard deviation by
measuring the standard error.
Standard error is always less
than standard deviation
SE gets smaller as n grows
sdoes not change!
SE measures the uncertainty
in location of mean
s measures spread in data
t-Distributions

If we know s then setting a confidence interval on how
well our sample mean X measures the true mean is
easy:
z
x m
s
n

But – if we don’t know s then we estimate use the tdistribution:
X m
t
s
n
Closer look at t-distributions


The t-distribution looks
very much like the
Normal distribution and
as the number of degrees
of freedom (df) gets large
the two become
indistinguishable
t-distribution tables are
used much the same way
as N(0,1) – major
difference is the df value
X m
t
s
n
Example…

You are inspecting a shipment of 10 000
precision machined rods to be used in an engine
assembly plant. You select a random sample of
20 and measure the diameters. You find that the
average diameter of the sample is 5.465 cm with
a standard deviation in the measurements of
0.005 cm. It is critical that the diameters do not
exceed 5.471 cm. You are willing to accept a
1% failure rate. Should you accept the
shipment?
Solution:


This would be an example of a 1-tailed tdistribution, a = 0.01, t19,0.01= 2.539
A 1% failure rate looks like this:
Test the numbers…
This implies that
99.998% of the
sample will not
exceed the
threshold diameter
 Accept!

X  5.471cm
m  5.465 cm
s  0.005 cm
(5.471  5.465)
t
 5.231
0.005
19
Two-tailed t-Tests



In the previous example we
looked at whether or not the
diameter was less than a
maximum allowable value.
Just as we have done earlier
with confidence intervals we
can also specify a maximum
allowable range (“plus or
minus”) for our mean.
Let’s test the mean diameter
at a 95% confidence level that
is implied by our measurement
Use following formula:
x  tn1,a / 2
s
s
 m  x  tn1,a / 2
n
n
Margin of
error

We measured mean diameter as 5.645 cm, s =
0.005 so the upper and lower margins are:
tn 1,a / 2

s
0.005
 (2.093)
 0.0024
n
19
We can be 95% confident that the diameters of
the parts are in the range (5.463,5.467) cm
Example 7.9


Plot data:
Identify variables, etc:
 df
= (50-1) = 49
 a = 0.05
 m = 23.56, s = 12.52
 t = 2.009

Interval = (20.00,27.12)
?
X m
t
s
n
Example of a Matched Pairs t-test:
Exercise 7.40

Formulate appropriate
hypotheses
 H0:
no difference
 Ha: LH > RH

Re-arrange data:
 find
m and s (see next page)
Ho: m = 0
 df = 25 - 1 = 24
 Find t  X  m  2.844

s
n
 Use
Excel =tdist(t, df, #tails)
 Use Table D
The probability of the null
hypothesis is only 0.004
 LH thread takes longer

Robustness…

A statistical test is considered robust if:
 It
is insensitive to deviations from original
assumptions being made. This could include
smaller sample size or deviation from
normality
Rules of thumb – When to use the
t-test
• Small sample sizes (n≈15) and
close to normal
• Mid range sample size (n ≥ 15) as
long as distribution not strongly
skewed and no outliers
• Large sample size (n > 40) even if
skewed or with some outliers
Fine print: Rules of thumb do not obviate the need to always inspect your data! Stemplots or histograms
give you insight into just how “skewed” or “outlier-riddled” is your data. Always know what the data set
looks like before applying tests.
In conclusion…




Read 7.1 carefully – we skipped over some
terms and discussions of applicability of the ttest
Be sure you understand when (and why) we
need the t-test
Know the difference between standard deviation
and Standard Error
Try: 7.4, 7.12, 7.26, 7.42