Download temptature measurements

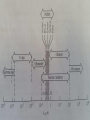
TEMPTATURE
MEASUREMENTS
CHAPTER 8
GROUP 3:
JALAL ALSHAKHS
EDUARD ISCSENKO
RYAN ORDIA UNUIGBOJE
MATERIAL FROM THEORY AND DESIGN FOR MECHANICAL MEASUREMENTS;
TEMPERATURE STANDARDS:
“Temperature can be loosely described as the property of an object that
describes its hotness or coldness, concepts that are clearly relative. Our
experiences indicate that heat transfer tends to equalize temperature; or
more precisely, systems that are in thermal communication will eventually
have equal temperatures. The zeroth law of thermodynamics states that two
systems in thermal equilibrium with a third system are in thermal equilibrium
with each other. Although the zeroth law of thermodynamics essentially
provides the definition of equality of temperature, it provides no means for
defining a temperature scale.”
TEMPERATURE STANDARDS:
Fixed points temperatures and interpolation:
A temperature scale provides for three essential aspects of
temperature measurement:
• The definition of the size of the scale increment,
• Fixed reference points for establishing known temperatures
• A means for interpolating between these fixed temperature points.
TEMPERATURE MEASUREMENTS
Interpolation:
• The calibration of a temperature measurement device entails not only
the establishment of fixed temperature points, but the indication of
any temperature between fixed points.
• The operation of a mercury-in-glass thermometer is based on the
thermal expansion of mercury contained in a glass capillary, where
the level of the mercury is read as an indication of the temperature.
TEMPERATURE STANDARDS
• Submerge the thermometer in
water at the ice point, make a
mark on the glass at the height
of the column of mercury, and
label it 0o C.
• Submerge the thermometer in
boiling water, and mark the level
of mercury, and label it 100 o
Figliola, 2000 C.
TEMPERATURE STANDARDS
• The process of establishing 50oC without a fixed point calibration is called
interpolation.
• Theory of the behavior of the mercury in the thermometer, or many fixed
points for calibration are necessary.
• Even by the late 18th century, there was no standard for interpolating
between fixed points on the temperature scale; the result was that different
thermometers indicated different temperatures away from fixed points,
sometimes with surprisingly large errors.
TEMPRATURE
• Temperature is one of the most commonly measured engineering
variables.
• Thermometry is based on thermal expansion.
• Most materials exhibit a change in size as a result of a change on
temperature.
• Measure temperature variation through thermal expansion of liquid in
glass.
• Difference in thermal expansion between liquid and glass results in a
change in level.
TEMPERATURE
• The modern engineering definition of the temperature scale is
provided by a standard called the International Temperature Scale.
• This standard establishes fixed points for temperature and provides
standard procedures and devices for interpolating between fixed
points.
TEMPERATURE
• A liquid-in-glass thermometer
measures temperature by virtue of
the thermal expansion of liquid.
•
The liquid is contained in a glass
structure that consists of a bulb and
a stem.
•
The bulb serves as a reservoir and
provides sufficient fluid for the total
volume change of the fluid to cause
a detectable rise of the liquid in the
stem.
TEMPERATURE
During calibration, the thermometer is subject to one of three
measuring environments:
• Complete immersion thermometer
• Total immersion thermometer
• Partial immersion thermometer
BI-METALLIC THERMOMETER
• Based on differential thermal expansion of two metals
• Two different materials are bonded together
• At bonding temperature, the metals are straight
BI-METALLIC THERMOMETER
• Rc ∝ d / [(C∝)A – (C∝)B](T2 - T1)
Rc = radius of curvature
C∝ = material thermal expansion coefficient
T = temperature
d = thickness
• INVar is common material where : C∝ = 1.7 * 10-8 m/mo C
• Where steel : C ∝ = 2*10-5 to 20*10-5 m/moC
ELECTRICAL RESISTANCE THERMOMETRY
• By physical nature of the conduction of electricity, electrical resistance of a
conductor varies with temperature.
• Two basic classes of sensor
– Resistance temperature detectors (RTD)
• Electrical conductors
– Thermistors
• Semiconductors
ELECTRICAL RESISTANCE THERMOMETRY
• The physical basis for the relationship between resistance and temperature is the temperature
dependence of the resistivity of the material, ρ e.
• The resistance of a conductor length l and cross-sectional area A c may be expressed in terms of
resistivity: •
• R = ρ el / A c
Where:
R = Resistance
ρe = resistivity of material (temp dependent)
l = length
Ac = cross-sectional area
• The resistance temperature detector (RTD) is constructed by
mounting a metal wire on an insulating support structure to eliminate
mechanical strain and by encasing the wire to prevent changes in
resistance due to sensor’s environment, such as corrosion.
• Mechanical strains change a conductor’s resistance and must be
eliminated for accurate temperature measurements are to be made.
ELECTRICAL RESISTANCE THERMOMETRY
• Over small temperature ranges, R = Ro [1 + ∝(T – To)]
• Ro= reference resistance at To ; ∝= coefficient of resistivity.
• Helical coils provide strain relief as the conductor expands and
contracts. Platinum is the most popular.
RESISTANCE MEASUREMENTS
• Platinum is the most linear over the entire region.
• Platinum RTD’s are used over a wide range from cryogenic to ≈ 650o
C with uncertainty at ± 0.005o C possible
RESISTANCE MEASUREMENTS
• The choice of an appropriate resistance measuring device must be
made based on the required level of uncertainty in the final
temperature measurement.
• Conventional ohmmeters cause a small current to flow during
resistance measurements, creating self-heating in the RTD. – An
appreciable temperature change of the sensor may be caused by this
current, in effect a loading error.
RESISTANCE MEASUREMENTS
• Bridge circuits are used to measure the resistance of RTDs, to
minimize loading errors, and to provide low uncertainties in measured
resistance values.
• Wheatstone bridge circuits are commonly used for these
measurements. – However, the basic Wheatstone bridge circuit does
not compensate for the resistance of the leads in measuring
resistance of an RTD, which are a major source of error in electrical
resistance thermometers.
BRIDGE CIRCUITS
•
Use a Wheatstone bridge with
conductor length
compensation.
•
the figure shows a 3-wire
Callender-Griffith bridge circuit.
Leads 1, 2, 3 have resistance
r1, r2, r3, where r2 does not
affect the circuit, since there is
no current through the
galvometer at balance
conditions.
BRIDGE CIRCUITS
• At balanced condition, iG = 0
R1/R2 = R3/RRTD
with lead wire then : R1/R2 = (R3 + r1)/ (RRTD + r3)
If R1 = R2 then RRTD = R3 + r1 – r3
• If r1 balances r3 :
RRTD = R3
RTD has a slow response time and may not be suitable in transit conditions.
THERMISTOR
• Thermally sensitive resistors
• They are ceramic-like semi-conductor devices. Resistance decreases
rapidly with decreasing temperature
– R = Roe β (1/T - 1/To)
“β ranges from 3500k to 4600k depending on device material and
construction”
• This equation is valid over limited temperature range, unless β(t) is given.
Typically, β is constant for set temperature range.
THERMISTOR
• Thermistors are generally used in applications where high sensitivity,
ruggedness, or fast response times are necessary.
• High resistance of thermistors eliminates the lead length
compensation issues found in RTD. However, thermistors are not
directly interchangeable, due to variation in β and sensitivity to
temperature change.
THERMOELECTRIC TEMPERATURE
MEASUREMENT
• The most common temperature sensing and control element is the
thermocouple.
• Consists of two electrical conductors, made of dissimilar materials
joined together at a junction.
• The output is a voltage that is related to the temperature at the
junction.
• The thermoelectric phenomena is a result of simultaneous flow of heat
and electricity away from the junction.
THERMOELECTRIC TEMPERATURE
MEASUREMENT
• If T1 ≠ T2, a finite electric potential emf1 exists whose magnitude
depends on ∆T and the difference in materials.
THERMOELECTRIC TEMPERATURE
MEASUREMENT
• “In an electrical conductor that is subject to a temperature gradient, there will be both a
flow of thermal energy and a flow of electricity. Both of these phenomena are closely tied
to the behavior of the free electrons in a metal; it is no coincidence that good electrical
conductors are, in general, good thermal conductors. The characteristic behavior of these
free electrons in an electrical circuit composed of dissimilar metals results in a useful
relationship between temperature and emf.”
• Three effects can occur:
1. Seebeck effect
2. Peltier effect
3. Thomson effect
SEEBECK EFFECT
• Seebeck effect – generation of voltage potential as a result of
temperature difference between two junctions in circuit. It is a fixed
and reproducible relationship between emf and junction temp T1 and
T2
• Seebeck coefficient: ∝AB = [∂(emf) / ∂T]open circuit
• This is a measure of the rate of change of voltage of the two materials,
with respect to temperature, and is the static sensitivity of the open
circuit thermocouple.
SEEBECK EFFECT
• Under ideal conditions, the measured emf of thermocouple is due to
Seebeck effect, alone.
• Should be measured with no current flow through use of high
impedance measurement device.
PELTIER EFFECT
• In Peltier effect, heat must be removed at I2R to maintain temperature of
conductor. At the junction, extra heat is generated (Peltier heat),which is
proportional to I.
PELTIER EFFECT
• The Peltier effect is due to the thermodynamically reversible
conversion of energy as a current flows across the junction, in
contrast to the irreversible dissipation of energy associated with I2 R
losses.
• The proportionality constant is the Peltier coefficient πAB, and the
heat transfer required to maintain a constant temperature is: Qπ =
πABI
• If I ≈ 0, heat ≈ 0
THOMPSON EFFECT
•
The conductor has
temperature gradient and
potential difference, there is a
flow of heat and current.
• To maintain constant
temperature, an amount of
heat must be removed
different from I2R.
• Qσ = σI (T1-T2)
• σ = Thompson coef
FUNDAMENTAL THERMOCOUPLE LAWS
The use of thermocouple circuits to measure temperature
is based on observed behaviors of carefully controlled
thermocouple materials and circuits. The following laws
provide the basis necessary for temperature measurement
with thermocouples:
FUNDAMENTAL THERMOCOUPLE LAWS
Law of homogeneous materials: A thermoelectric current cannot be sustained in a
circuit
of a single homogeneous material by the application of heat alone, regardless of
how it
might vary in cross section. Simply stated, this law requires that at least two
materials be
used to construct a thermocouple circuit for the purpose of measuring
temperature. It is
interesting to note that a current may occur in an inhomogeneous wire that is
nonuniformly
heated; however, this is neither useful nor desirable in a thermocouple.
FUNDAMENTAL THERMOCOUPLE LAWS
Law of intermediate materials: The algebraic sum of the thermoelectric forces in a
circuit
composed of any number of dissimilar materials is zero if all of the circuit is at a
uniform
temperature. This law allows a material other than the thermocouple materials to be
inserted
into a thermocouple circuit without changing the output emf of the circuit. As an
example,
consider the thermocouple circuit shown in Figure where the junctions of the
measuring device are made of copper and material B is an alloy (not pure copper). The
electrical connection between the measuring device and the thermocouple circuit
forms yet
another thermocouple junction. The law of intermediate materials, in this case,
FUNDAMENTAL THERMOCOUPLE LAWS
FUNDAMENTAL THERMOCOUPLE LAWS
Law of successive or intermediate temperatures: If two dissimilar homogeneous
materials
that form a thermocouple circuit produce emf1 when the junctions are at T1 and T2
and
produce emf2 when the junctions are at T2 and T3, the emf generated when the
junctions are
at T1 and T3 will be emf1 þ emf2. This law allows a thermocouple calibrated for one
reference temperature, say T2, to be used at another reference temperature, such as
T3, to
determine temperature T1.
REFERENCE JUNCTIONS
• Thermocouples can be used to
measure the temperature
difference between two junctions of
dissimilar material. One junction at
reference temperature, the other at
measured temperature.
– Ice bath of crushed ice and water
is common.
REFERENCE JUNCTIONS
• Law of intermediate materials ensures that the extension wires on
potentiometer do not effect emf as long as they are at the same
temperature.
• The reference junction must be at a known temperature, be
reproducible, and be stable. Ice point 0 o C is common, although it is
only relatively stable.
• Electronic reference junctions are available on some measurement
devices, which use a thermister to measure local environment
THERMOCOUPLE DESIGNATIONS
• Thermocouples are made from many different combinations of
materials.
•
Choice of thermocouple depends on temperature range, application
environment, and desired uncertainty level.
VOLTAGE OUTPUT
• The slope of the curve
corresponds to the static
sensitivity of the thermocouple
circuit.
•
The output emf voltage of a
thermocouple can be
interpreted either from
conversion tables or by
polynomial expressions that
are fitted to a particular type
of thermocouple.
THERMOCOUPLE MEASUREMENT
• The Seebeck voltage can be measured at no current flow. If current is
flowing in circuit, Thomson and Peltier effects may be experienced.
• The ideal is to use either a potentiometer or a high impedance digital
voltmeter which results in minimal current flow.
•
In common applications, a “built-in electronic cold junction compensation”
method is used, which employs the use of a thermister. Typical error is 0.5o
to 1.5o bias.
•
Internal polynomial interpolation is often used to convert from voltage to
temperature, which introduces a linearization error.
THERMOCOUPLE MEASUREMENT
• Often gains of 100 to 500 are used to boost the thermo-electric signal
to a range detectable by A/D board.
• Typical use of differential-ended inputs with twisted pair conductors
and a 10kΩ to 100kΩ resistor between low input (-) terminal and lowlevel ground.
MULTIPLE-JUNCTION THERMOCOUPLE
CIRCUITS
• More than two junctions can be employed in a thermocouple circuit,
and thermocouple circuits can be devised to measure temperature
differences or average temperature or to amplify the output voltage of
a thermocouple circuit.
THERMOPILES
• “Thermopile” is a term used to describe a multiple-junction
thermocouple circuit that is designed to amplify the output of the
circuit.
• Increasing the voltage output may be a key element in reducing the
uncertainty in the temperature measurement.
• This figure shows a
thermopile for providing an
amplified output signal; in
this case, the output voltage
would be N times the single
thermocouple output, where
N is the number of measuring
junctions in the circuit.
• The average output voltage
corresponds to the average
temperature level sensed by
the N junctions
THERMOCOUPLES
When spatially averaged
temperature is desired,
multiple thermocouple
junctions can be
arranged as shown:
DATA ACQUISITION CONSIDERATIONS
• Attention must be given to the cold junction compensation method.
• The two connection points of the thermocouple to the DAS board form
two new thermocouple connections.
• Use of external cold junction methods between the thermocouple and
the board will eliminate this problem, but more frequently, the
thermocouple will be connected directly to the board and use built-in
electronic cold junction compensation.
DATA ACQUISITION CONSIDERATIONS
• This is usually accomplished by using a separate thermistor sensor, which
measures the temperature at the system connection point to determine the
cold junction error, and providing an appropriate bias voltage correction
either directly or through software.
• These boards also may use internal polynomial interpolation for converting
measured voltage into temperature.
• This introduces a “linearization” error, which is a function of thermocouple
material and temperature range and typically specified with the DAS board.
DATA ACQUISITION CONSIDERATIONS
• Thermocouple wire pairs should be twisted to reduce noise.
• A differential-ended connection is preferred between the
thermocouple and the DAS board.
• The thermocouple becomes an isolated voltage source, meaning
there is no longer a direct ground path keeping the input within its
common mode range.
• As a consequence, a common complaint is that the measured signal
may drift or suddenly jump in the level of its output
DATA ACQUISITION CONSIDERATIONS
• This interference behavior is eliminated by placing a 10-k Ω to 100-k Ω
resistor between the low terminal of the output and low-level ground.
• Since most DAS boards use A/D converters having a ± 5V full scale,
the signal must be conditioned using an amplifier.
• Usually, a gain of 100 to 500 is significant.
• High gain, very low noise amplifiers are important for accurate
measurements.
DATA ACQUISITION CONSIDERATIONS
• Thermocouples tend to have long time constant relative to the typical
sample rate capabilities of general purpose DAS boards.
• If temperature measurements show greater then expected
fluctuations, high-frequency sampling noise is a likely cause.
• Slowing down the sample rate or using a smoothing filter are simple
solutions.
• The period of averaging should be on the scale of the time constant of
the thermocouple.
RADIATIVE TEMPERATURE MEASUREMENTS
•
RADIATIVE TEMPERATURE MEASUREMENTS
•
RADIATIVE TEMPERATURE MEASUREMENTS
• Radiation Detectors:
Radiative energy flux can be detected in a sensor by two basic
techniques. First one involves a thermal detector in which absorbed radiative
energy elevates the detector temperature. The equilibrium temperature of the
detector is a direct measure of the amount of radiation absorbed. The
resulting rise in temperature must then be measured. Second type relies on
interaction of a photon with an electron, resulting in an electric current. In a
photomultiplier tube, the emitted electrons are accelerated and used to
create an amplified current, which is measured.
RADIATIVE TEMPERATURE MEASUREMENTS
• Radiometer:
Perhaps the simplest form, a
radiometer, measures a source temperature
by measuring the voltage output from a
thermopile detector. It would have a
hemispherical field of view, and measures
both the direct or beam radiation, and diffuse
radiation.
RADIATIVE TEMPERATURE MEASUREMENTS
• Pyrometry:
Optical pyrometry identifies the
temperature of a surface by its color, or
more precisely the color of the radiation it
emits. The major advantage of an optical
pyrometer lies in its ability to measure high
temperatures remotely. For many
applications this provides a safe and
economical means of measuring high
temperatures.
RADIATIVE TEMPERATURE MEASUREMENTS
• Optical Fiber Thermometers:
The optical fiber thermometer is based on the creation of an ideal
radiator that is optically couple to a fiber-optic transmission system. The
operating range of this thermometer is 300￮ to 1900￮C. Signal transmission is
accomplished using standard, low-temperature fiber optics. A specific
wavelength band of the transmitted radiation is detected and measured, and
these raw data are reduced to yield the temperature of the blackbody sensor.
The measurement system has superior frequency response and sensitivity.
The system has been employed for measurement in combustion applications.
Temperature resolution of 0,1 mK is possible.
PHYSICAL ERRORS IN TEMPERATURE
MEASUREMENT
• In general errors in temperature measurement derive from two
fundamental sources. The first source of errors derive from uncertain
information about the temperature of the sensor itself. Such
uncertainties can result from random interpolation errors,
collaboration systematics errors or a host of other sources. However
errors in temperature measurements can still occur even if the sensor
was measured exactly. In such case , the probe does not sense
accurately the temperature it was intended to measure.
INSERTION ERROR
This discussion focuses on ensuring that a sensor output accurately
represents the temperature it is intended to measure. The thermometer
is subject to the very sources of error we wish to describe and analyze.
The thermometer, very simply indicates its own temperature. The
physical mechanism that may cause a temperature probe to indicate a
temperature different from that intended include conduction, radiation
and velocity recovery errors.
CONDUCTION ERRORS
Errors that result from conduction heat transfer between the measuring
environment and the ambient are often immersion errors. The
fundamental nature of the errors created by conduction in measured
temperature can be illustrated by the model of a temperature probe
shown in the picture. The essential physics of immersion errors
associated with conduction can be discerned by modeling the
temperature probe as a fin.
RADIATION ERRORS
In the presence of significant radiation heat transfer, the equilibrium
temperature of a temperature probe may be different from the fluid
temperature being measured. The error due to radiation can be
estimated by considering steady-state thermodynamic equilibrium
conditions for a temperature sensor. A first law analysis of a system
containing the probe, at steady-state conditions, yields:
RADIATION SHIELDING
Radiation shielding is a key concept in controlling radiative heat
transfer; shielding for radiation is analogous to insulation to reduce
conduction heat transfer. A radiation shield is an opaque surface
interposed between a temperature sensor and its radiative
surroundings so as to reduce electromagnetic wave interchange
RECOVERY ERRORS IN TEMPERATURE
MEASURMENTS
The kinetic energy of a gas moving at high velocity can be converted to
sensible energy by reversibly and adiabatically bringing the flow to
rest at a point. The temperature resulting from this process is called
the stagnation or total temperature T. On the other hand, the static
temperature of the gas is the temperature that would be measured by
an instrument moving at the local fluid velocity.
SUMMARY
Temperature is a very important quantity in both engineering and
Science in concept and application. It also one of the most widely
measured engineering variable for different sectors on a basis of variety
of control and safety systems. Temperature is defined for practical
purposes through the establishments of a temperature scale like the
Kelvin Scale containing fixed reference points and interpolation.
Two common methods of temperature measurements are
Thermocouples and Resistance Temperature Detectors(RTD).
Installation effects on the accuracy of the temperature are direct results
of the influence of radiation, conduction and convection heat transfer
on the equilibrium temperature of a temperature sensor.