* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download temptature measurements
Survey
Document related concepts
Transcript
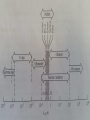
TEMPTATURE MEASUREMENTS CHAPTER 8 GROUP 3: JALAL ALSHAKHS EDUARD ISCSENKO RYAN ORDIA UNUIGBOJE MATERIAL FROM THEORY AND DESIGN FOR MECHANICAL MEASUREMENTS; TEMPERATURE STANDARDS: “Temperature can be loosely described as the property of an object that describes its hotness or coldness, concepts that are clearly relative. Our experiences indicate that heat transfer tends to equalize temperature; or more precisely, systems that are in thermal communication will eventually have equal temperatures. The zeroth law of thermodynamics states that two systems in thermal equilibrium with a third system are in thermal equilibrium with each other. Although the zeroth law of thermodynamics essentially provides the definition of equality of temperature, it provides no means for defining a temperature scale.” TEMPERATURE STANDARDS: Fixed points temperatures and interpolation: A temperature scale provides for three essential aspects of temperature measurement: • The definition of the size of the scale increment, • Fixed reference points for establishing known temperatures • A means for interpolating between these fixed temperature points. TEMPERATURE MEASUREMENTS Interpolation: • The calibration of a temperature measurement device entails not only the establishment of fixed temperature points, but the indication of any temperature between fixed points. • The operation of a mercury-in-glass thermometer is based on the thermal expansion of mercury contained in a glass capillary, where the level of the mercury is read as an indication of the temperature. TEMPERATURE STANDARDS • Submerge the thermometer in water at the ice point, make a mark on the glass at the height of the column of mercury, and label it 0o C. • Submerge the thermometer in boiling water, and mark the level of mercury, and label it 100 o Figliola, 2000 C. TEMPERATURE STANDARDS • The process of establishing 50oC without a fixed point calibration is called interpolation. • Theory of the behavior of the mercury in the thermometer, or many fixed points for calibration are necessary. • Even by the late 18th century, there was no standard for interpolating between fixed points on the temperature scale; the result was that different thermometers indicated different temperatures away from fixed points, sometimes with surprisingly large errors. TEMPRATURE • Temperature is one of the most commonly measured engineering variables. • Thermometry is based on thermal expansion. • Most materials exhibit a change in size as a result of a change on temperature. • Measure temperature variation through thermal expansion of liquid in glass. • Difference in thermal expansion between liquid and glass results in a change in level. TEMPERATURE • The modern engineering definition of the temperature scale is provided by a standard called the International Temperature Scale. • This standard establishes fixed points for temperature and provides standard procedures and devices for interpolating between fixed points. TEMPERATURE • A liquid-in-glass thermometer measures temperature by virtue of the thermal expansion of liquid. • The liquid is contained in a glass structure that consists of a bulb and a stem. • The bulb serves as a reservoir and provides sufficient fluid for the total volume change of the fluid to cause a detectable rise of the liquid in the stem. TEMPERATURE During calibration, the thermometer is subject to one of three measuring environments: • Complete immersion thermometer • Total immersion thermometer • Partial immersion thermometer BI-METALLIC THERMOMETER • Based on differential thermal expansion of two metals • Two different materials are bonded together • At bonding temperature, the metals are straight BI-METALLIC THERMOMETER • Rc ∝ d / [(C∝)A – (C∝)B](T2 - T1) Rc = radius of curvature C∝ = material thermal expansion coefficient T = temperature d = thickness • INVar is common material where : C∝ = 1.7 * 10-8 m/mo C • Where steel : C ∝ = 2*10-5 to 20*10-5 m/moC ELECTRICAL RESISTANCE THERMOMETRY • By physical nature of the conduction of electricity, electrical resistance of a conductor varies with temperature. • Two basic classes of sensor – Resistance temperature detectors (RTD) • Electrical conductors – Thermistors • Semiconductors ELECTRICAL RESISTANCE THERMOMETRY • The physical basis for the relationship between resistance and temperature is the temperature dependence of the resistivity of the material, ρ e. • The resistance of a conductor length l and cross-sectional area A c may be expressed in terms of resistivity: • • R = ρ el / A c Where: R = Resistance ρe = resistivity of material (temp dependent) l = length Ac = cross-sectional area • The resistance temperature detector (RTD) is constructed by mounting a metal wire on an insulating support structure to eliminate mechanical strain and by encasing the wire to prevent changes in resistance due to sensor’s environment, such as corrosion. • Mechanical strains change a conductor’s resistance and must be eliminated for accurate temperature measurements are to be made. ELECTRICAL RESISTANCE THERMOMETRY • Over small temperature ranges, R = Ro [1 + ∝(T – To)] • Ro= reference resistance at To ; ∝= coefficient of resistivity. • Helical coils provide strain relief as the conductor expands and contracts. Platinum is the most popular. RESISTANCE MEASUREMENTS • Platinum is the most linear over the entire region. • Platinum RTD’s are used over a wide range from cryogenic to ≈ 650o C with uncertainty at ± 0.005o C possible RESISTANCE MEASUREMENTS • The choice of an appropriate resistance measuring device must be made based on the required level of uncertainty in the final temperature measurement. • Conventional ohmmeters cause a small current to flow during resistance measurements, creating self-heating in the RTD. – An appreciable temperature change of the sensor may be caused by this current, in effect a loading error. RESISTANCE MEASUREMENTS • Bridge circuits are used to measure the resistance of RTDs, to minimize loading errors, and to provide low uncertainties in measured resistance values. • Wheatstone bridge circuits are commonly used for these measurements. – However, the basic Wheatstone bridge circuit does not compensate for the resistance of the leads in measuring resistance of an RTD, which are a major source of error in electrical resistance thermometers. BRIDGE CIRCUITS • Use a Wheatstone bridge with conductor length compensation. • the figure shows a 3-wire Callender-Griffith bridge circuit. Leads 1, 2, 3 have resistance r1, r2, r3, where r2 does not affect the circuit, since there is no current through the galvometer at balance conditions. BRIDGE CIRCUITS • At balanced condition, iG = 0 R1/R2 = R3/RRTD with lead wire then : R1/R2 = (R3 + r1)/ (RRTD + r3) If R1 = R2 then RRTD = R3 + r1 – r3 • If r1 balances r3 : RRTD = R3 RTD has a slow response time and may not be suitable in transit conditions. THERMISTOR • Thermally sensitive resistors • They are ceramic-like semi-conductor devices. Resistance decreases rapidly with decreasing temperature – R = Roe β (1/T - 1/To) “β ranges from 3500k to 4600k depending on device material and construction” • This equation is valid over limited temperature range, unless β(t) is given. Typically, β is constant for set temperature range. THERMISTOR • Thermistors are generally used in applications where high sensitivity, ruggedness, or fast response times are necessary. • High resistance of thermistors eliminates the lead length compensation issues found in RTD. However, thermistors are not directly interchangeable, due to variation in β and sensitivity to temperature change. THERMOELECTRIC TEMPERATURE MEASUREMENT • The most common temperature sensing and control element is the thermocouple. • Consists of two electrical conductors, made of dissimilar materials joined together at a junction. • The output is a voltage that is related to the temperature at the junction. • The thermoelectric phenomena is a result of simultaneous flow of heat and electricity away from the junction. THERMOELECTRIC TEMPERATURE MEASUREMENT • If T1 ≠ T2, a finite electric potential emf1 exists whose magnitude depends on ∆T and the difference in materials. THERMOELECTRIC TEMPERATURE MEASUREMENT • “In an electrical conductor that is subject to a temperature gradient, there will be both a flow of thermal energy and a flow of electricity. Both of these phenomena are closely tied to the behavior of the free electrons in a metal; it is no coincidence that good electrical conductors are, in general, good thermal conductors. The characteristic behavior of these free electrons in an electrical circuit composed of dissimilar metals results in a useful relationship between temperature and emf.” • Three effects can occur: 1. Seebeck effect 2. Peltier effect 3. Thomson effect SEEBECK EFFECT • Seebeck effect – generation of voltage potential as a result of temperature difference between two junctions in circuit. It is a fixed and reproducible relationship between emf and junction temp T1 and T2 • Seebeck coefficient: ∝AB = [∂(emf) / ∂T]open circuit • This is a measure of the rate of change of voltage of the two materials, with respect to temperature, and is the static sensitivity of the open circuit thermocouple. SEEBECK EFFECT • Under ideal conditions, the measured emf of thermocouple is due to Seebeck effect, alone. • Should be measured with no current flow through use of high impedance measurement device. PELTIER EFFECT • In Peltier effect, heat must be removed at I2R to maintain temperature of conductor. At the junction, extra heat is generated (Peltier heat),which is proportional to I. PELTIER EFFECT • The Peltier effect is due to the thermodynamically reversible conversion of energy as a current flows across the junction, in contrast to the irreversible dissipation of energy associated with I2 R losses. • The proportionality constant is the Peltier coefficient πAB, and the heat transfer required to maintain a constant temperature is: Qπ = πABI • If I ≈ 0, heat ≈ 0 THOMPSON EFFECT • The conductor has temperature gradient and potential difference, there is a flow of heat and current. • To maintain constant temperature, an amount of heat must be removed different from I2R. • Qσ = σI (T1-T2) • σ = Thompson coef FUNDAMENTAL THERMOCOUPLE LAWS The use of thermocouple circuits to measure temperature is based on observed behaviors of carefully controlled thermocouple materials and circuits. The following laws provide the basis necessary for temperature measurement with thermocouples: FUNDAMENTAL THERMOCOUPLE LAWS Law of homogeneous materials: A thermoelectric current cannot be sustained in a circuit of a single homogeneous material by the application of heat alone, regardless of how it might vary in cross section. Simply stated, this law requires that at least two materials be used to construct a thermocouple circuit for the purpose of measuring temperature. It is interesting to note that a current may occur in an inhomogeneous wire that is nonuniformly heated; however, this is neither useful nor desirable in a thermocouple. FUNDAMENTAL THERMOCOUPLE LAWS Law of intermediate materials: The algebraic sum of the thermoelectric forces in a circuit composed of any number of dissimilar materials is zero if all of the circuit is at a uniform temperature. This law allows a material other than the thermocouple materials to be inserted into a thermocouple circuit without changing the output emf of the circuit. As an example, consider the thermocouple circuit shown in Figure where the junctions of the measuring device are made of copper and material B is an alloy (not pure copper). The electrical connection between the measuring device and the thermocouple circuit forms yet another thermocouple junction. The law of intermediate materials, in this case, FUNDAMENTAL THERMOCOUPLE LAWS FUNDAMENTAL THERMOCOUPLE LAWS Law of successive or intermediate temperatures: If two dissimilar homogeneous materials that form a thermocouple circuit produce emf1 when the junctions are at T1 and T2 and produce emf2 when the junctions are at T2 and T3, the emf generated when the junctions are at T1 and T3 will be emf1 þ emf2. This law allows a thermocouple calibrated for one reference temperature, say T2, to be used at another reference temperature, such as T3, to determine temperature T1. REFERENCE JUNCTIONS • Thermocouples can be used to measure the temperature difference between two junctions of dissimilar material. One junction at reference temperature, the other at measured temperature. – Ice bath of crushed ice and water is common. REFERENCE JUNCTIONS • Law of intermediate materials ensures that the extension wires on potentiometer do not effect emf as long as they are at the same temperature. • The reference junction must be at a known temperature, be reproducible, and be stable. Ice point 0 o C is common, although it is only relatively stable. • Electronic reference junctions are available on some measurement devices, which use a thermister to measure local environment THERMOCOUPLE DESIGNATIONS • Thermocouples are made from many different combinations of materials. • Choice of thermocouple depends on temperature range, application environment, and desired uncertainty level. VOLTAGE OUTPUT • The slope of the curve corresponds to the static sensitivity of the thermocouple circuit. • The output emf voltage of a thermocouple can be interpreted either from conversion tables or by polynomial expressions that are fitted to a particular type of thermocouple. THERMOCOUPLE MEASUREMENT • The Seebeck voltage can be measured at no current flow. If current is flowing in circuit, Thomson and Peltier effects may be experienced. • The ideal is to use either a potentiometer or a high impedance digital voltmeter which results in minimal current flow. • In common applications, a “built-in electronic cold junction compensation” method is used, which employs the use of a thermister. Typical error is 0.5o to 1.5o bias. • Internal polynomial interpolation is often used to convert from voltage to temperature, which introduces a linearization error. THERMOCOUPLE MEASUREMENT • Often gains of 100 to 500 are used to boost the thermo-electric signal to a range detectable by A/D board. • Typical use of differential-ended inputs with twisted pair conductors and a 10kΩ to 100kΩ resistor between low input (-) terminal and lowlevel ground. MULTIPLE-JUNCTION THERMOCOUPLE CIRCUITS • More than two junctions can be employed in a thermocouple circuit, and thermocouple circuits can be devised to measure temperature differences or average temperature or to amplify the output voltage of a thermocouple circuit. THERMOPILES • “Thermopile” is a term used to describe a multiple-junction thermocouple circuit that is designed to amplify the output of the circuit. • Increasing the voltage output may be a key element in reducing the uncertainty in the temperature measurement. • This figure shows a thermopile for providing an amplified output signal; in this case, the output voltage would be N times the single thermocouple output, where N is the number of measuring junctions in the circuit. • The average output voltage corresponds to the average temperature level sensed by the N junctions THERMOCOUPLES When spatially averaged temperature is desired, multiple thermocouple junctions can be arranged as shown: DATA ACQUISITION CONSIDERATIONS • Attention must be given to the cold junction compensation method. • The two connection points of the thermocouple to the DAS board form two new thermocouple connections. • Use of external cold junction methods between the thermocouple and the board will eliminate this problem, but more frequently, the thermocouple will be connected directly to the board and use built-in electronic cold junction compensation. DATA ACQUISITION CONSIDERATIONS • This is usually accomplished by using a separate thermistor sensor, which measures the temperature at the system connection point to determine the cold junction error, and providing an appropriate bias voltage correction either directly or through software. • These boards also may use internal polynomial interpolation for converting measured voltage into temperature. • This introduces a “linearization” error, which is a function of thermocouple material and temperature range and typically specified with the DAS board. DATA ACQUISITION CONSIDERATIONS • Thermocouple wire pairs should be twisted to reduce noise. • A differential-ended connection is preferred between the thermocouple and the DAS board. • The thermocouple becomes an isolated voltage source, meaning there is no longer a direct ground path keeping the input within its common mode range. • As a consequence, a common complaint is that the measured signal may drift or suddenly jump in the level of its output DATA ACQUISITION CONSIDERATIONS • This interference behavior is eliminated by placing a 10-k Ω to 100-k Ω resistor between the low terminal of the output and low-level ground. • Since most DAS boards use A/D converters having a ± 5V full scale, the signal must be conditioned using an amplifier. • Usually, a gain of 100 to 500 is significant. • High gain, very low noise amplifiers are important for accurate measurements. DATA ACQUISITION CONSIDERATIONS • Thermocouples tend to have long time constant relative to the typical sample rate capabilities of general purpose DAS boards. • If temperature measurements show greater then expected fluctuations, high-frequency sampling noise is a likely cause. • Slowing down the sample rate or using a smoothing filter are simple solutions. • The period of averaging should be on the scale of the time constant of the thermocouple. RADIATIVE TEMPERATURE MEASUREMENTS • RADIATIVE TEMPERATURE MEASUREMENTS • RADIATIVE TEMPERATURE MEASUREMENTS • Radiation Detectors: Radiative energy flux can be detected in a sensor by two basic techniques. First one involves a thermal detector in which absorbed radiative energy elevates the detector temperature. The equilibrium temperature of the detector is a direct measure of the amount of radiation absorbed. The resulting rise in temperature must then be measured. Second type relies on interaction of a photon with an electron, resulting in an electric current. In a photomultiplier tube, the emitted electrons are accelerated and used to create an amplified current, which is measured. RADIATIVE TEMPERATURE MEASUREMENTS • Radiometer: Perhaps the simplest form, a radiometer, measures a source temperature by measuring the voltage output from a thermopile detector. It would have a hemispherical field of view, and measures both the direct or beam radiation, and diffuse radiation. RADIATIVE TEMPERATURE MEASUREMENTS • Pyrometry: Optical pyrometry identifies the temperature of a surface by its color, or more precisely the color of the radiation it emits. The major advantage of an optical pyrometer lies in its ability to measure high temperatures remotely. For many applications this provides a safe and economical means of measuring high temperatures. RADIATIVE TEMPERATURE MEASUREMENTS • Optical Fiber Thermometers: The optical fiber thermometer is based on the creation of an ideal radiator that is optically couple to a fiber-optic transmission system. The operating range of this thermometer is 300○ to 1900○C. Signal transmission is accomplished using standard, low-temperature fiber optics. A specific wavelength band of the transmitted radiation is detected and measured, and these raw data are reduced to yield the temperature of the blackbody sensor. The measurement system has superior frequency response and sensitivity. The system has been employed for measurement in combustion applications. Temperature resolution of 0,1 mK is possible. PHYSICAL ERRORS IN TEMPERATURE MEASUREMENT • In general errors in temperature measurement derive from two fundamental sources. The first source of errors derive from uncertain information about the temperature of the sensor itself. Such uncertainties can result from random interpolation errors, collaboration systematics errors or a host of other sources. However errors in temperature measurements can still occur even if the sensor was measured exactly. In such case , the probe does not sense accurately the temperature it was intended to measure. INSERTION ERROR This discussion focuses on ensuring that a sensor output accurately represents the temperature it is intended to measure. The thermometer is subject to the very sources of error we wish to describe and analyze. The thermometer, very simply indicates its own temperature. The physical mechanism that may cause a temperature probe to indicate a temperature different from that intended include conduction, radiation and velocity recovery errors. CONDUCTION ERRORS Errors that result from conduction heat transfer between the measuring environment and the ambient are often immersion errors. The fundamental nature of the errors created by conduction in measured temperature can be illustrated by the model of a temperature probe shown in the picture. The essential physics of immersion errors associated with conduction can be discerned by modeling the temperature probe as a fin. RADIATION ERRORS In the presence of significant radiation heat transfer, the equilibrium temperature of a temperature probe may be different from the fluid temperature being measured. The error due to radiation can be estimated by considering steady-state thermodynamic equilibrium conditions for a temperature sensor. A first law analysis of a system containing the probe, at steady-state conditions, yields: RADIATION SHIELDING Radiation shielding is a key concept in controlling radiative heat transfer; shielding for radiation is analogous to insulation to reduce conduction heat transfer. A radiation shield is an opaque surface interposed between a temperature sensor and its radiative surroundings so as to reduce electromagnetic wave interchange RECOVERY ERRORS IN TEMPERATURE MEASURMENTS The kinetic energy of a gas moving at high velocity can be converted to sensible energy by reversibly and adiabatically bringing the flow to rest at a point. The temperature resulting from this process is called the stagnation or total temperature T. On the other hand, the static temperature of the gas is the temperature that would be measured by an instrument moving at the local fluid velocity. SUMMARY Temperature is a very important quantity in both engineering and Science in concept and application. It also one of the most widely measured engineering variable for different sectors on a basis of variety of control and safety systems. Temperature is defined for practical purposes through the establishments of a temperature scale like the Kelvin Scale containing fixed reference points and interpolation. Two common methods of temperature measurements are Thermocouples and Resistance Temperature Detectors(RTD). Installation effects on the accuracy of the temperature are direct results of the influence of radiation, conduction and convection heat transfer on the equilibrium temperature of a temperature sensor.