Download Lesson 19 - Ampere`s Law As Modified by Maxwell

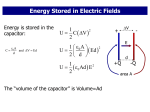
Lesson 19 - Ampere's Law As Modified by Maxwell
I.
Capacitor Problem
In the figure below, we attempt to apply Ampere's law for a wire leading to a
capacitor using the curve, C.
C

E
Ic
Ic
Although it is easy to write Ampere's Law, we find that we have a paradox since
the value for the integral depends on the current that penetrates any surface
bounded by the curve.
 
 Bd s μ I
o
p
C
For a circular membrane, the current passing through the surface is Ic.
For a surface that wraps around the capacitor, we have no current
penetrating the surface.
In 1865, James Clerk Maxwell, one of the great physicists of all times, solved this
paradox and developed electromagnetic theory (one of the major branches of
physics).
II.
Ampere's Law As Modified By Maxwell
The current flowing through the wire supplies the charge on the plates of the
capacitor that produces the electric field across the capacitor plates. From our
previous work with parallel plate capacitors, we have

ε
A


  E d 
q CV 
d   





From the definition of current, we have
i c  dq 
dt
Maxwell's contribution was to imagine that the changing electric flux between the
capacitor was equivalent to a physical current as far as the creation of a magnetic
field. He called this "fictitious" current the displacement current.
To remove the paradox, Maxwell equated the displacement current to the current
in the wire and modified the right hand side of Ampere's Law to include the sum
of the real current and the displacement current.
Id 
 
Φ


B

d
s

μ
I

I

μ
I

μ
ε


o
p
o p
o o
d



t
E
C
In our work, there is no difference for our parallel plate capacitor between the
partial derivative of the electric flux with respect to time and the full time
derivative of the electric flux. However, Maxwell using more powerful
mathematical techniques solved the problem in general thereby showing that it is
the partial derivative of the electric flux with respect to time. Thus, we have
written our final result so that it will be correct for all problems.
IMPORTANT: This incredible result states that there is a second way to create a
circulating magnetic field: A time varying electric flux!! We will return later in the
course to this wonderful result and its importance in communications.