Download Section 3.4 Basic Functions

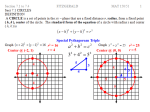
Special Pythagorean Triple
r2 = 16
a2  b2  c2
r=4
Center @ (0, 0)
Center @ (-2, 1)
32  4 2  5 2
5
4
3
5
4 3
4
4
r2 = 25
r=5
34
4
5
5
4
5
(___, 0)
Substitute in 0 for y and solve for x.
x  22  0  12  16
x  22  1  16
x  22  15
x  2   15
x  2  15
 2 
 2  15,0
15 ,0;  2  15 ,0
(0, ___)
Substitute in 0 for x and solve for y.
0  22   y  12  16
2
4   y  1  16
 y  12  12
y  1   12
y  1 2 3
0,1  2 3 
0,1  2 3 ; 0,1  2 3 
( h, k )
x  h2   y  k 2  r 2
x  12   y   22  r 2
x  12   y  22  r 2
4  12  2  22  r 2
32  42  r 2
9  16  25  r
2
Substitute in h and k as 1 and -2.
Substitute in x and y as 4 and 2.
Solve for r2.
x  12   y  22  25
Write the standard equation of a circle with the endpoints of
the diameter as ( -2, 7) and ( -14, -9).
( x, y )
GENERAL FORM OF THE EQUATION OF A CIRCLE:
Graph x  y  4 x  6 y  9  0 Convert to
Group x terms and y terms together and
move the constant to the other side.
2
2
x  h2   y  k 2  r 2
by completing the square.
x 2  4 x  y 2  6 y  9
Complete the square of the x’s and y’s.
(+2)2  y 2  6 y  ___
(-3)2  9  ___
4  ___
9
x 2  4 x  ___
x
y
x
y

 
x  22   y  32  4
Graph

Center @ (-2, 3)
2 x 2  2 y 2  12 x  8 y  24  0
r2 = 4
r=2
Divide everything by 2. Why?
x 2  y 2  6 x  4 y  12  0
(-3)2  y 2  4 y  ___
(-2)2  12  ___
9  ___
4
x 2  6 x  ___



x
x  32   y  22  25

y
Center @ (3, 2)
x
x 2  y 2  ax  by  c  0
y
r2 = 25
r=5
x 0
y a
x
2
y (-a)
x
x   y  a  0   y  a
2
2
2
2
2
Square both sides to remove radical.
x2   y  a  y  a
FOIL the binomials.
x 2  y 2  2ay  a 2  y 2  2ay  a 2
2
Focus
Cancel like terms on each side.
a
a
2a
x 2  2ay  2ay
Solve for x2.
4a
a
-a
-a
Directrix
2
x 2  4ay
Graph the following equations.
y  12 x
2
x=-3
The y is squared and the coefficient
on the x is positive, the parabola
opens to the right. 4a = 12, a = 3 and
the vertex is at (0, 0).
6
V
3
F
6
Graph the following equations.
x 2  16 y
The x is squared and the coefficient
on the y is negative, the parabola
y=4
opens down. 4a = -16, a = -4 and the
vertex is at (0, 0).
V
4
8
F
8
Graph the following equations.
y 2  8 x
x=2
The y is squared and the coefficient
on the x is negative, the parabola
opens to the left. 4a = -8, a = -2 and
the vertex is at (0, 0).
4
F
V
2
4
Graph the following equations.
x  2
2
 8 y  1
The x is squared and the coefficient
on the y is positive, the parabola
opens up. 4a = 8, a = 2 and the
vertex is at (2, -1).
4
F
2
y=-3
V
4
Graph the following equations.
y 2  2 y  4 x  17  0
x=3
We need to complete the square of
the y-terms to put in graphing form.
Isolate the y-terms.
1
y 2  2 y  (-1)
___2  4 x  17  ___
 y  1
2
 4 x  16
Factor out the 4 as the GCF.
 y  1
2
 4x  4
The y is squared and the coefficient
on the x is positive, the parabola
opens to the right. 4a = 4, a = 1 and
the vertex is at (4, 1).
V
2
F
2
Graph the following equations.
x2  6x  4 y  1  0
We need to complete the square of
the x-terms to put in graphing form.
Isolate the x-terms.
9
x 2  6 x  (+3)
___2 4 y  1  ___
x  3
2
 4y 8
Factor out the 4 as the GCF.
x  3
2
 4 y  2 
2
F
y=-3
The x is squared and the coefficient
on the y is positive, the parabola
opens up. 4a = 4, a = 1 and the
vertex is at (-3, -2).
V
2
Equation format is ... …plug in x & y to solve for 4a.
Draw a rough graph.
(2,3)
Draw a rough graph.
V

V(-4, ?)
9  4a 2 
9
 4a
2
Equation format is ... …distance from V to F is 1, a = 1,
2
y  k  4a x  h and plug in the vertex values.



F
Draw a rough graph.
F(-4, 4)
3
y = -2
32  4a2
y 2  4ax
9
2
y  x
2
Equation format is ...
x  h 2  4a y  k 
4–3=1
V(-4, 1)
 y   22  41x   1
 y  22  4x  1
…distance from F to the directrix
line is 6, V is halfway, so a = 3. Plug
in a and the vertex values.
x   42  43 y  1
x  42  12 y  1