Download Parabolas

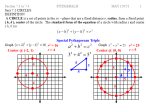
ALGEBRA 2 Conic Sections!
Shedding Some Light on our
FIRST conic section ---The
Parabola
A parabola is the set of all points P
in the plane that are equidistant
from a fixed point F (focus) and a
fixed line d (directrix).
Which Way? The squared terms’
axis is opposite from the way it
lays!
https://youtu.be/04nBaKx9wiM
STANDARD Form
x  h 
2
 4 p y  k   y  k   4 px  h 
• UP/DOWN parabola
(Function)
• Vertex ( h, k)
• Axis of symmetry is parallel
to the y-axis (x=h)
• ( h, k + p) is the FOCUS
• If p > 0, then it opens up
• If p < 0, the parabola opens
down
• DIRECTRIX: y = k - p
• length of The Focal Chord
=4|p|
2
• SLEEPING parabola (NonFunction)
• Vertex (h, k)
• Axis of symmetry is parallel
to the x-axis (y=k)
• (h + p, k) is the FOCUS
• If p > 0 then it opens right
• If p < 0, the parabola opens
left
• DIRECTRIX: x = h - p
• length of The Focal Chord
=4|p|
How Can We Graph x2= 6y?
•
VERTEX?
•
The vertex will be at the origin
•
“P” OR “C” VALUE=
•
Since 4p = 6 , p = 3/2
•
WHICH WAY?
•
Since the “x” is squared and the
“p” is positive, this parabola will
open UP!
•
FOCUS?
•
Our focus is “p” units from the
vertex, in the direction of
opening F (0, 3/2)
•
DIRECTRIX?
•
Our directrix is a line “p” units
behind the curve: y = -3/2
•
FOCAL CHORD END POINTS?
•
The Focal Chord gives us an idea
of the width of the parabola at
the focus: 2p each way ( 3,3/2 ) and (3, 3/2)
x2= 6y
Working Backwards—What do you
know? Where can you go?
• Find the standard form of the equation of
the parabola with a directrix at y = -2 and
focus (0, 2) .
When in Doubt, Sketch it OUT!
x  h 
2
 4 p y  k 
x  4 py
2
x  8y
2
Not in Standard Form? Completing the
Square will take you there!
• With a parabola, there is
only one “family” to
complete! Just make sure
that the lead coefficient is
equal to one. (divide, if
needed!)
• Remember—the squared
term’s “family” stands alone
on one side of the equation.
• Take half the linear terms
coefficient to find your
factor– square it—and
complete the “family”.
• Add this value to both sides
to balance the equation.
• Finally, Factor out the
leading coefficient—to “wrap
up” the linear side.
x  4x  4 y  8  0
2
x 2  4 x  __  4 y  8  __
x  2
2
x  2
2
x  2
2
 4 y  4
 4 y  1
• Rearrange your terms—
The Squared term’s
family stands alone!
• Divide both sides by the
lead coefficient.
• Complete the
Square…Adding this value
to both sides of your
equation!
• FACTOR each side!
An Alternate Form