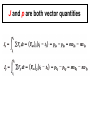* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Momentum, Impulse and Collision
Old quantum theory wikipedia , lookup
Hunting oscillation wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Monte Carlo methods for electron transport wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Equations of motion wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Classical mechanics wikipedia , lookup
Angular momentum operator wikipedia , lookup
Photon polarization wikipedia , lookup
Centripetal force wikipedia , lookup
Mass in special relativity wikipedia , lookup
Atomic theory wikipedia , lookup
Matter wave wikipedia , lookup
Mass versus weight wikipedia , lookup
Center of mass wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Specific impulse wikipedia , lookup
Classical central-force problem wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
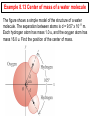
Chapter 8 Momentum, Impulse, and Collisions Goals for Chapter 8 • To determine the momentum of a particle • To add time and study the relationship of impulse and momentum • To see when momentum is conserved and examine the implications of conservation • To use momentum as a tool to explore a variety of collisions • To understand the center of mass • To study rocket propulsion Introduction • If you watch a football game, you’ll see collisions, tackles, many men colliding at once, maybe just two in an open area. Are these situations different? • Newton told us the forces result in acceleration of a mass. We will now study two new points of view— momentum and impulse. 8.1 How does momentum relate to mass and velocity? • Understanding momentum begins with the simple relationship that momentum is equal to mass multiplied by velocity. p x mv x p y mv y p z mv z The units of the magnitude of momentum are units of mass times speed: kg∙m/s. The plural of momentum is “momenta.” Don’t forget that momentum is a vector Newton’s 2nd Law in terms of Momentum dp F dt • The net force (vector sum of all forces) acting on a particle equals the time rate of change of momentum of the particle. • According to the equation, a rapid change momentum requires a large net force, while a gradual change in momentum requires less net force. Impulse • The impulse, denoted by J, is defined to be the product of the net force F, acting on an object for a time period ∆t: J F t (when force is constant) t2 J Fdt (General Definition of Impulse) t1 • Impulse is a vector quantity; its direction is the same as the net force ∑F. The SI unit of impulse is the newton-second (N∙s). Because 1 N = 1 kg∙m/s2, an alternative set of unit for impulse is kg∙m/s, the same as the unit of momentum. The Impulse-Momentum Theorem J p 2 p1 The change in momentum of a particle during a time interval equals to the impulse of the net force that J acts on the particle during that interval. • the impulse-momentum theorem is valid even when the net force varies with time. The area under in F-t graph equals to J = ∆p J and p are both vector quantities Compare momentum and kinetic energy • The impulse– momentum relationship depends on time of an impact while the work-energy theorem focuses on the distance of force application. Example 8.1 Momentum versus kinetic energy The iceboats have masses m and 2m, and the wind exerts the same constant horizontal force F on each ice boat. The two iceboats start from rest and cross the finish line a distance s away. 1. Which iceboat crosses the finish line with greater kinetic energy? 2. Which iceboat crosses the finish line with greater momentum? Example 8.2 A ball hits a wall Suppose you throw a ball with a mass of 0.40 kg against a brick wall. It hits the wall moving horizontally to the left at 30 m/s and rebounds horizontally to the right at 20 m/s. a. Find the impulse of the net force on the ball during its collision with the wall. b. If the ball is in contact with the wall for 0.010 s, find the average horizontal force that he wall exerts on the ball during the impact. Copyright © 2008 Pearson Education Inc., publishing as Pearson Addison-Wesley Example 8.3 Kicking a soccer ball • A soccer ball has a mass of 0.40 kg. initially, it is moving to the left at 20 m/s, but then it is kicked and given a velocity at 45o upward and to the right, with a magnitude of 30 m/s. Find the impulse of the net force and the average net force, assuming a collision time ∆t = 0.010 s. Test Your Understanding 8.1 Rank the following situations according to the magnitude of the impulse of the net force, from largest value to smallest value. In each situation a 1000-kg automobile is moving along a straight east-west roads i. The automobile is initially moving east at 25 m/s and comes to a stop in 10 s. ii. The automobile is initially moving east at 25 m/s and comes to a stop in 5 s. iii. The automobile is at rest, and a 2000 N net force toward is applied to it for 10 s. iv. The automobile is initially moving east at 25 m/s, and a 2000 N net force toward is applied to it for 10 s v. The automobile is initially moving east at 25 m/s. Over a 30 s period, the automobile reverses direction and ends up moving west at 25 m/s. 8.2 Conservation of momentum • If the vector sum of the external forces on a system is zero, the total momentum of the system is constant. It is a direct consequence of Newton’s 3rd law. CAUTION conservation of momentum means conservation of its components If the vector sum of the external forces on the system is zero, then Px, Py, and Pz are all constant. Conservation of momentum vs. conservation of mechanical energy • Conservation of momentum is more general than the principle of conservation of mechanical energy. • Mechanical energy is conserved only when the internal forces are conservative but conservation of momentum is valid even when the internal forces are not conservative. Example 8.4 Recoil of a rifle • A marksman holds a rifle of mass mR = 3.00 kg loosely in his hands, so as to let it recoil freely when fired. He fires a bullet of mass mB = 5.00 g horizontally with a velocity relative the ground of vRx = 300 m/s. what is the recoil velocity vRx of the rifle? What are the final momentum and kinetic energy of the bullet? Of the rifle? Example 8.5 Collision along a straight line Two gliders move toward each other on a frictionless linear air track. After they collide, glider B moves away with a final velocity of +2.0 m/s. what is the final velocity of glider A? How do the changes in momentum and in velocity compare for the two gliders? Example 8.6 Collision in a horizontal plane Two battling robots sliding on a frictionless surface. Robot A, with mass 20 kg, initially moves at 2.0 m/s parallel to the x-axis. It collides with robot B, which has mass 12 kg and is initially at rest. After the collision, robot A is moving at 1.0 m/s in a direction that makes an angle α = 30o with its initial direction. What is the final velocity of robot B? Check your understanding • A spring-loaded toy sits at rest on a horizontal frictionless surface. When the spring releases, the toy breaks into three equal-mass pieces, A,B, and C, which slide along the surface, piece A moves off the negative x-direction, while piece B moves off in the negative y–direction. 1. What are the signs of the velocity components of piece C? 2. Which of the three pieces is moving the fastest? 8.3 Momentum Conservation and Collisions • In physics, we broaden the meaning the term collision to include any strong interaction between bodies that lasts a relatively short time. If the forces between the bodies are much larger than external forces, as is the case in most collisions, we can neglect the external forces and treat the bodies as an isolated system, the momentum is conserved during a collision. Elastic Collision • If the forces between the bodies are conservative during a collision, then the total kinetic energy of the system is the same after the collision as before. Such a collision is called an elastic collision. Inelastic Collision • A collision in which the total kinetic energy after the collision is different (most time is less) than before the collision is called an inelastic collision. Completely inelastic collision • In a completely inelastic collision, the two bodies stick together after the collision, they are the same final velocity v2: • In a completely inelastic collision, the momentum is conserved but the kinetic energy is lost – kinetic energy after the collision is less than the kinetic energy before the collision. Caution: an inelastic collision doesn’t have to be completely inelastic. Only in elastic collisions, the total kinetic energy before equals the total kinetic energy after. Example 8.7 A completely inelastic collision Suppose we repeat the collision describe in Example 8.5, but this time equip the gliders so that they stick together instead of bouncing apart after they collide. Find the common final x-velocity v2x, and compare the initial and final kinetic energies. Example 8.8 The ballistic pendulum A bullet, with mass mB, is fired into a block of wood with mass mW, suspended like a pendulum, and makes a completely inelastic collision with it. After the impact of the bullet, the block swings up to a maximum height y. Given the values of y, mB, and mW, what is the initial speed v1 of the bullet? Example 8.9 An automobile collision A 1000 kg compact car is traveling north at 15 m/s when it collides with a 2000 kg truck traveling east at 10 m/s. All occupants are wearing seat belts and there are no injuries, but the two vehicles are thoroughly tangled and move away from the impact point as one mass. The insurance adjustor has asked you to find the velocity of the wreckage just after impact. What do you tell her? Test Your Understanding 8.3 • For each situation, state whether the collision is elastic or inelastic. If it is inelastic, state whether its completely inelastic. 1. You drop a ball from your hand. It collides with the floor and bounces back up so that is just reaches your hand. 2. You drop a different ball from your hand and let it collide with the ground. This ball bounces back up the half the height from which it was dropped. 3. You drop a ball of clay from your hand. When it collides with the ground, it stops. 8.4 Elastic Collisions An elastic collision in an isolated system is one in which kinetic energy as well as momentum is conserved. Elastic collisions occur when the forces between the colliding bodies are conservative. 1 1 1 1 2 2 2 2 m A v A1x m B v B1x m A v A 2 x m B v B 2 x 2 2 2 2 m A v A1x m B v B1x m A v A2 x mB v B 2 x Where vA1x and vB1x are x-velocities before the collision, and vA2x and vB2x are x-velocities after the collision. Elastic collisions – One body initially at rest 1 1 1 2 2 2 m A v A1x m A v A2 x m B v B 2 x 2 2 2 m A v A1x m A v A2 x mB v B 2 x v A2 x m A m B v A1x m A mB vB2 x 2m A v A1x m A mB If mA = mB, then vA2x = 0 and vB2x = vA1x. That is, the body that was moving stops dead; it gives all its momentum and kinetic energy to the body that was at rest. Elastic collisions and relative velocity In a straight-line elastic collision of two bodies, the relative velocities before and after the collision have the same magnitude but opposite sign. v B 2 x v A2 x (v B1x v A1x ) Example 8.10 An elastic straight-line collision We repeat the air-track experiment from Example 8.5, but now we add ideal spring bumpers to the gliders so that the collision is elastic. What are the velocities of A and B after the collision? Example 8.11 Moderator in a nuclear reactor The fission of uranium nuclei in a nuclear reactor produces high-speed neutrons. Before a neutron can trigger additional fissions, it has to be slowed down by collisions with nuclei in the moderator of the reactor. Suppose a neutron (mass 1.0 u) traveling at 2.6 x 107 m/s undergoes a head-on elastic collision with a carbon nucleus (mass 12 u) initially at rest. The external forces during the collision are negligible. What are the velocities after the collision ( 1u = 1.66 x 10-27 kg) Example 8.12 A two-dimensional elastic collision The figure shows an elastic collision of two pucks on a frictionless air-hockey table. Find the final speed vB2 of puck B and the angles α and β in the figure. Test Your Understanding 8.4 • Most present-day nuclear reactors use water as a moderator. Are water molecules (mass mw = 18.0 u) a better or worse moderator than carbon atoms? (one advantage of water is that it also acts as a coolant for the reactor’s radioactive core.) 8.5 Center of Mass • Suppose we have several particles with masses m1, m2, and so on. Let the coordinates of m1 be (x1,y1), those of m2 be (x2,y2), and so on, we define the center of mass of the system as the point that has coordinates (xcm, ycm) given by xcm m1 x1 m2 x2 m3 x3 m1 m2 m3 mx m i i i i i ycm m y m2 y2 m3 y3 1 1 m1 m2 m3 my m i i i i i In statistical language, the center of mass is a mass-weighted average position of the particles. Example 8.13 Center of mass of a water molecule The figure shows a simple model of the structure of a water molecule. The separation between atoms is d = 9.57 x 10-11 m. Each hydrogen atom has mass 1.0 u, and the oxygen atom has mass 16.0 u. Find the position of the center of mass. Many centers of mass Motion of center of mass • When the net external force acting on the wrench is zero, the center of mass moves in a straight line with constant velocity. Total momentum is conserved. dp dv m 0 dt dt • If the net external force on a system of particles is not zero, dv dp Fext Macm M dt dt Example 8.14 A tug-of-war on the ice James and Ramon are standing 20.0 m apart on the slippery surface of a frozen pond. Ramon has mass 60.0 kg and James has mass 90.0 kg. Midway between the two man a mug of their favorite beverage sits on the ice. They pull on the ends of a light rope that is stretched between them. When James has moved 6.0 m toward the mug, how far and in what direction has Ramon moved? • A shell explodes into two fragments in flight. If air resistance is ignored, the center of mass continues on the same trajectory as the shell’s path before exploding. • The same effect occurs with exploding fireworks. Test Your Understanding 8.5 • Will the center of mass in the figure continue on the same parabolic trajectory even after one of the fragments hits the ground? Why or why not? No. If the gravity is the only force acting on the system of two fragments, the center of mass will follow the parabolic trajectory of a freely falling object. Once a fragment lands, the ground exerts a normal force on that fragment.