Download exponential and logarithm functions and derivatives: 1.logarithms

* exponential and logarithm functions and derivatives:
1.logarithms(log):
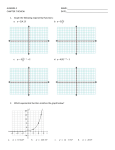
y =
a is normally a number greater than 1 (although it need only be
greater than 0 and not equal to 1). The function is defined for
all x > 0. Here is its graph for any base a.
Note the following:
• For any base, the x-intercept is 1. Why? The logarithm of 1 is 0. y =
• The graph passes through the point (a, 1). Why? The logarithm of the
base is 1. Loga a= 1.
*the graph is below x-axis ,the logarithm is negative for 0<x<1.
.the function is defined for positive values of
x,
.
.the range of function is all real numbers.
.the negative y-axis is a vertical asymptote.
Important relation
Properties:
x=
2.natural logarithims(ln)
Y=ln x ,ln1=0 ,ln 0=
Domain={x:x>o},
range={all real numbers}
Properties: ln 1=0;
Ln =ln 1- ln x= -ln x ;ln(xy)=ln x+ln y
2.exponential functions:
a-The exponential function with positive base a > 1 is the
function
It is defined for every real number x. Here is its graph:
There are two important things to note:
• The y-intercept is at (0, 1). For, a0 = 1.
• The negative x-axis is a horizontal asymptote. For, when x is a large
negative number -- e.g. b−10,000 -- then y is a very small positive number.
Properties:
,
b- y=
;
;
;
;
Ex: Let f(x) = ex. Write the function f(−x)and draw it .
F(-x)=
(the argument x is replaced by –x)
The graph of y=
is the reflection of y= ex
Important relations:
A-
2.
From 1 &2 let f(x)=
F(g(x))=
and g(x)=
and g(f(x))=
a the functions : f(x)=
B- f(x)=lnx and
g(x)=
&
g(x)=
therefore for any base
are inverses
F(g(x))=ln
g(f(x))=
=x ;lne=1
;
; therefore f(x)= ln x and g(x)=
are inverses Here are the graphs of y = ex and y = ln x :
CD- ln a=b
a=
Ex: find 1.
1.
b=-2 ;
2.
;
?
3.
Ex: evaluate the following:
1.
2.ln
=x+1 3.1og 106.2=6.2 4.
Ex: solve the equations:1.
{to release x+1 from exponent take the inverse function (the logarithm
with base 5) of both sides as}
X+1=4
2.
x-4=x
; x=3
(take log of base 2 or 3 for both sides)
;x- x
=4; x=
3.
Take the inverse function 5x of both sides ;let each sides be the exponent
with base 5 as:
2x+3=125 ;2x=125-3 ;x=61
4.ln(5x-1)=ln(2x+8) take exponent with base e for each sides;
*Derivative of logatithm and exponent functions:
2.
1.
Or y=
(
3.
*lnu)=
4.
Ex :derivative the following :
1.y=ln
*3
2.y=
3.y=
4.
;
+lnx*3