* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Section 4 Seesaws Hello. I`m Lou Bloomfield and welcome to How
Survey
Document related concepts
Angular momentum operator wikipedia , lookup
Fictitious force wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Jerk (physics) wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Rotational spectroscopy wikipedia , lookup
Equations of motion wikipedia , lookup
Center of mass wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Classical central-force problem wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Mass versus weight wikipedia , lookup
Transcript
Section 4 Seesaws
Hello. I'm Lou Bloomfield and welcome to How Things Work at the University of Virginia.
Today's topic: Seesaws. Seesaws are a simply toy that consists of a long board mounted on
a central pivot. Two riders get on opposite ends of that board, and adjust their positions
until the seesaw balances. At that point then, they can begin to make the seesaw rock back
and forth. Either by leaning toward or away from the pivot, or by pushing on the ground
with their feet.
Mechanically, a seesaw is a lever and fulcrum seesaws also work as a simple example of a
mechanical system with two equilibrium positions one side is stable, while the other is unstable
Levers can be used to exert a large force over a small distance at one end by exerting only a small
force over a greater distance at the other.
Classification
Industry
Weight
Fuel source
Components
Simple machine
Construction
Mass times gravitational acceleration
potential and kinetic energy {mechanical energy}
fulcrum or pivot, load and effort
http://en.wikipedia.org/wiki/Lever
When I was a kid, seesaws were everywhere. Any playground worth its salt had a couple of
them. And either at recess or during a birthday party we'd clamber onto the seesaws, one
at each end, maybe one big kid, one little kid, maybe several at each end. And we'd rock
back and forth furiously until our legs wore out, or one of us got hurt. Or we simply wanted
to do something else.
Nowadays, seesaws become rarer and rarer. It seems that either they're risky, or perhaps
modern children don't enjoy that sort of activity as much.
Whatever the reason, they're missing an opportunity to experiment with rotational motion,
balance, levers, and mechanical advantage.
Seesaws turn out to be a wonderful context in which to explore the physics of rotational
motion.
So I've stuck with them, even as they've somewhat abandoned me. If you have a seesaw
nearby, I urge you to experiment with it. Although be safe, because there are ways in which
you can get yourself injured playing with a seesaw. More on that later.
If you don't have a see-saw, well, you can make one yourself. All you need is some object to
serve as a central pivot and a board to balance on that pivot. You adjust the spacings just so
and. Voila, a seesaw.
You can have it rock back and forth, just like the real thing. Actually, that simplicity.
The fact that you can make something like this so easily, explains why seesaws have been
around so long. They're pretty simple to make.
As I suggested earlier, the story of seesaws is also the story of rotational motion, balance,
levers, and mechanical advantage. We'll study those concepts here in the context of
seesaws and then use them repeatedly as we continue to look at how things work.
Before continuing, however, I want to ask you a question to think about. Not to answer, but
something you should have in mind as we work our way through the story of seesaws. It's a
difficult question, one that doesn't have an obvious answer so it's a good prelude to the rest
of the story here on seesaws.
Suppose you and a child half your height lean out over a swimming pool at the same
angle. So here's you, here's the child, and you're both leaning out over the swimming
pool at the same angle. If you both let go at the same moment, so that you begin to
rotate into the pool, which of the two of you reaches the water first?
To help guide us through the science of see saws, we'll pursue six, how and why questions.
How does a balanced seesaw move?
Why does a seesaw need a pivot?
Why does a lone seesaw rider plummet to the ground?
Why do the riders' weights and positions affect the seesaw's motion?
Why do the riders' distances from the pivot affect the seesaw's responsiveness?
How do the seesaw's riders affect one another?
There is one video sequence for each of those questions and a summary sequence at the
end.
And now onto the first question.
Part 1.
How does a balanced seesaw move?
The full answer to that question will require some careful explaining, but a short answer is
that a balanced seesaw rotates steadily about a fixed axis.
Now it's tempting to think that I've just asked a trick question, that a balanced seesaw
doesn't move at all. In fact, that it's horizontal and motionless.
But the real answer to that question is more subtle. Yes, a balanced seesaw can be
horizontal, and it can be motionless. But it doesn't have to be. What a balanced seesaw
does exhibit, however, is rotational inertia. If I set it spinning, it rotates steadily about a
fixed axis.
Up until now, I've talked about a type of motion that takes you from place to place. So, in
the episodes on skating, falling balls, and ramps we went somewhere; from place to place.
In this episode on seesaws, we don't go anywhere. Seesaws are installed in playgrounds.
And they stay there indefinitely. What seesaws do, do, however. Is rotate.
So, the world of motion can divide into two main types. The motion of translation, of
going somewhere and the motion of rotation, spinning in place. And see-saws. They're
about spinning in place.
In the episode on skating, we saw that a skater exhibits translational inertia. The inertia of
going places. And associated with that translational inertia was Newton's first law of
translational motion. Namely, that an object that's free of external forces, moves at
constant velocity.
In this episode on seesaws, we're looking at objects that can exhibit rotational inertia.
When they're at rest, they stay at rest. When they're rotating, they continue to rotate.
Associated with rotational inertia is another Newton's first law, but now it's the Newton's
first law of rotational motion.
In a draft form Newton's first law of rotational motion states that a rigid object that is not
wobbling and that is not experiencing any outside influences, rotates about a fixed axis
turning equal amounts in equal times.
That law has a couple of extra words in it. It refers only to rigid objects and objects that are
not wobbling.
So Newton's First Law of Rotational Motion has relatively limited applicability.
What can you do? Rotational motion simply is more complicated than translational motion
and therefore the Newton's 1st Law in the world of rotation is fairly limited. There are lots
of things that don't that don't follow Newton's 1st Law of rotational motion. Because they
either change shape, or because they're wobbling.
http://physics.bu.edu/~okctsui/PY105%20Lecture_notes/PY105_Fall2009_files/PY1056pm_NewtonLaw-Rotation.pdf
To perfect the draft of Newton's First Law of Rotational Motion, we need to identify the
external influences, and we need better language to describe rotation about a fixed axis
turning equal amounts and equal times.
I'm going to start with the second task.
In the previous episodes, I described translational motion and identified several physical
quantities that are useful for that description. Among those physical quantities were
position and velocity.
In describing rotational motion, there are analogous physical quantities. There is a physical
quantity describing... Angular position. Angular, rotational, it doesn't matter, but there, it's
technically called angular position. And there is a physical quantity describing how angular
position changes with time, and it's called angular velocity.
So, those are the 2 quantities I want to introduce.
1st, angular position.
Angular position is an object’s orientation, and instead of illustrating angular position using
the seesaw, I'm going to illustrate it using my body. So, angular position will describe how
I'm oriented.
I'm going to start with a zero of angular position, which is the starting point, the zero. This
will be my 0 of angular positioning, the orientation that we all agree is the starting point,
facing you.
If I change my angular position, that means that I'm facing some other direction, like this or
this or like this and Like that, and so on. Well, how do you describe, technically,
quantitatively, those various other orientations? How do you do it?
Actually, you need an amount and a direction. You need a vector. So angle position is a
vector quality and here's how it works.
First, the amount is an angle. The angle through which you have to rotate to go from the
zero, namely facing you, to the orientation that you're trying to describe.
For example this, this is the one I'm going to try to describe, facing like this. And the angle
that I have to rotate through to go from the zero, to this, is 90 degrees. From there to
there, that's 90 d-, you know what, 90 degrees right?
So this angular position is 90 degrees. But that's not enough. This is 90 degrees. And so is
this. And so is ……….this……, alright? So there are a bunch of 90 degree angles positions.
We need a direction as well. And the direction of an angular position is the axis about which
the rotation occurs. For example, to rotate to this 90 degree angular position, I need to
rotate about a vertical axis as though I were a toy top being spun. So I'm being spun, there I
go.
So this is 90 degrees about a vertical axis.
But there's an ambiguity. This is 90 degrees about a vertical axis. And so is this. They're
both 90 degrees about a vertical axis.
How do you distinguish them? Well, physicists and mathematicians distinguish them using a
convention known as the right-hand Rule. And the right-hand rule says that if you take your
fingers of your right hand and curl them in the direction in which the rotation occurs. For
example, if I'm going from this to this, the rotation is like that. Then look at my thumb. The
thumb of my right hand, points in the official direction of that rotation, downward.
So in going from 0 to this, I rotated 90 degrees. Downward.
On the other hand, if I go from this to this, my fingers have to be pointing the other way.
My thumb is now pointing up, this orientation this angular position is 90 degrees up.
So the ambiguity is solved by the right hand rule. 90 degrees down. And 90 degrees up.
How about this? That is 90 degrees toward you. And this is 90 degrees towards me.
Final word about angles. The angle part of angular position can be measured in various
units. Up until now, I've been using the unit known as the degree. It's a familiar unit of
angle; this is zero degrees, 90 degrees, 180 degrees, 270, 360.
Another possible unit of degree is the rotation. Full rotation: This is zero, quarter rotation,
half, three quarters, full rotation.
But the unit that mathematicians and physicists normally use to describe angles, is neither
of those two.
It's the radian. And there are two pi radians in a full rotation where pi is the mathematical
constant. Three point one four one five nine (3.14159) and so on. And that is the natural
unit of angles. There are reasons why it's particularly useful in physics. Whether you use it
or not, doesn't matter.
Pick your unit of angle and stick with it. You're fine.
So you can describe this angular position as 90 degrees down. Or quarter rotation down.
Or pi over two radians down. They're all the same.
That's angular position, but that by itself doesn't help us redraft Newton's first law of
rotational motion. We need to look a little deeper.
We have to look at how angular position is changing with time, because when something is
actually rotating its angular position is evolving, changing with time. And we need the next
physical quantity which is angular velocity.
Angular velocity is the rate at which angular position is changing with time.
So right now my angular position is not changing with time, so my angular velocity is zero.
But if I begin to spin, then my angular velocity is no longer zero. For example, if I turn like
this I am now turning about 90 degrees per second. And the same right hand rule applies.
I'm turning such that my fingers curl like this and my thumb points out. This is an angular
velocity of 90 degrees per second down. Also pi over two radians per second down.
Let me stop.
Let me show you 90 degrees up, here it is. Alright, I could show you 90 degrees toward you.
Yeah 90 degrees per second toward you but that's, I'm going to run out of ability to do this.
But I hope you get the point. That angle velocity describes how an object is rotated, that is
how fast it's going through angles, and also the axis about which it's spinning and finally,
using the right hand rule, the specific direction of its spin around that axis.
So you should be able now to distinguish 90 degrees per second down from 90 degrees per
second up.
That now, that physical quantity, angular velocity will be useful in redrafting Newton's first
law, rotation motion. Because we can rewrite the rotating about fixed axis, turning equal
amounts in equal times as, having constant angular velocity.
If I'm turning 90 degrees per second down and staying that way, my angular velocity is
constant.
Alright, that brings us to the other task. Which is identifying the external influences that
show up in Newton's first law of rotational motion. And those external influences are
twists. Technically, they're known as torques. A torque is the influence that upsets
rotational inertia. And therefore, violates Newton's first law of rotational motion.
We'll look more at torques. But just so that you know what a torque is. Let me show you
what happens when I exert a torque on this seesaw. To do it, I twist the see-saw. So I'll
grab the see-saw from the front, and I will twist. And suddenly, it changed its angular
velocity. - It started with an angular velocity of zero, let's get zero there. And it's now, at
present it is a rigid object that's not wobbly, it's obeying Newton's first law of rotational
motion.
But if I come in with an external influence of the right type, namely, a torque. While I'm
exerting that torque, it is not following Newton's first law of rotational motion. It changed
its angular velocity. So, we can now state Newton's first law of rotational motion in all its
glory.
A rigid object that is not wobbling and that is free of external torques rotates at constant
angular velocity.
That brings us to a question.
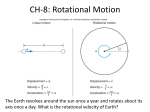
What influence or effect causes the earth to rotate steadily?
approximately 24 hours.
Turning once every,
The Earth is rotating because it exhibits rotational inertia. It's experiencing essentially no
torques, and therefore, it rotates according to Newton's 1st Law of Rotational Motion,
namely - It's a rigid object that is not wobbling, it is not experiencing any external torques,
so it rotates with constant angular velocity. That angular velocity is approximately one
rotation per 24 hours. About the North Pole so that the rotational axis points from the
centre of the earth up to the North Pole and that's the way the earth rotates.
So we see a balanced seesaw is not necessarily motionless or horizontal. What we can say
about that balanced seesaw however, is that it exhibits rotational inertia. If it's motionless,
it remains motionless. If it's rotating, it continues to rotate.
Because it's a rigid object that's not wobbling, it exhibits a particularly simple type of
rotational motion. Namely, constant angular velocity. So right now, the angular velocity of
this balanced seesaw Is 0. But if I twist it, and during the twist it's not rotationally inertial
and so, I'm violating Newton's 1st Law of rotational motion by doing the twist. Here we go,
I'll give it a twist. And now it's once again rotationally inertial. It's obeying Newton's 1st Law
of rotational motion. It's a rigid object that is not wobbling, it's free of external torques, so,
it rotates at constant angular velocity, apart from some air resistance problems here.
The point is, it's rotating right now, not because something is twisting it, but because
nothing is twisting it. It is its nature, and the nature of objects in our universe to keep
rotating in the absence of twists. They keep going. That's rotational inertia.
So, in a normal see-saw that perpetual rotation isn't possible, because during the rotation,
even when it's balanced initially, it eventually touches the ground. And at those moments
when it touches the ground, the ground exerts torques on the seesaw. It twists the seesaw
and therefore takes it out of Newton's First Law of Rotational Motion, violates Newton's
First Law of Rotational Motion, and new things happen. And those new things, basically the
consequences of torques... Are a subject for the next video.
Part 2.
Why does a seesaw need a pivot?
The answer to that question is that the pivot prevents the seesaw from undergoing translational
motion, while leaving it free to undergo rotational motion. Without a pivot to support its weight
and that of its riders, the seesaw would fall. And while two children might find it exciting to jump
out of an airplane seated at opposite ends of unsupported seesaw, that idea is unlikely to be popular
with their parents.
The physics will be fabulous but I'm not going to film it. I'm going to leave that for children who
enjoy extreme recess. Instead, I'm going to show you how an unsupported and riderless seesaw
moves.
Basically, I'm going to throw the seesaw through the air and we'll watch its motion. For obvious
reasons, I'm not going to use a large seesaw, I'm not even going to use one as big as this. But even
so, even with a small seesaw board, or a pretend seesaw board, I need more room, so, let's go
outside and have some fun.
I'm going to throw a riderless, unsupported seesaw.
Well that sure was quick.
But this is video so I can show you that throw again. And this time I can slow it down to one tenth its
original speed. Moreover, I can make the images of the seesaw linger on the screen so that you can
see all the previous images as the seesaw goes through its travels. Now, because the camera takes
30 frames per second, those images will be separated from one another by a thirtieth of a second.
Here we go.
The same throw, slowed down to one tenth its original speed, with all the previous images of the
seesaws lingering on the screen.
Seeing all those image of the seesaw is pretty, but how do we make sense of the seesaw's motion?
It turns out that the seesaw is doing two things at once, it's translating and it's rotating.
Translational motion.
Well, its centre of mass is traveling in the arc of a falling object as though it were a tiny ball located
at the centre of mass, that's traveling in the arc that we're familiar with for falling balls. At the same
time, the seesaw, which is an extended object, is rotating about its centre of mass, its natural pivot.
And, it's doing these two things at once: the translation motion of a falling object located right at its
centre of mass, and the rotational object. Motion of an extended object rotating about its natural
pivot. Its centre of mass.
So I'm going to show you that same video again, same throw. Once again, at one tenth normal
speed with all the previous images of the seesaw board in view, but this time, I'm going to show you
the arc of a falling object, and I picked the arc just right so that the seesaw's centre of mass will
travel along that arc, as the seesaw rotates about its own centre of mass located on that arc.
A seesaw has it's centre of mass located pretty much in its geometrical centre. So, the motion we
saw had the centre of the board travelling in the arc of a falling object as the rest of the board
rotated about its geometrical centre.
But not all objects have their centres of mass at their geometrical centres.
For example, a mallet. Nearly all of the mass of this mallet is in its head. The handle is almost
nothing. So, when I throw this mallet, the head will travel in the arc of a falling object because the
centre of mass is almost dead centre in that head. So you'll see that centre of mass travel in the arc,
and that's the head. At the same time, the handle, which is almost an insignificant contribution of
mass, will rotate about the centre of mass, and the arc'll look a little different.
So, now I'm going to throw the mallet. Here we go.
This rubber mallet has most of its mass in its head. Once again, that was very quick. So I'm going to
show you the same throw. But this time, I'm going to slow it down to one tenth its original speed.
And I'm going to let all the previous images of the mallet linger on the screen. So you can watch the
path the mallet takes. And its orientation while it's taking that path.
It's already pretty obvious that the mallet is following the arc of a falling object as its rotating. But
just to make that crystal clear. I'm going to show you the same throw again, one-tenth its original
speed, with all the images of the mallet lingering on the screen, but this time I am going show the
arc of a falling object that travels along in the path taken by the mallet's centre of mass.
So you see, when you throw something, and it becomes a falling object. That is, it's experiencing
only one force, its weight, its motion is actually fairly simple. The object's centre of mass travels in
the arc of a falling object. As though it were a simple thing like a falling ball. At the same time, the
rest of the object may be rotating about that centre of mass. The object's natural pivot. So the
object is doing two things at once. It's translating in the arc of a falling object as it's rotating in the
manner of an object that's just simply free to rotate about its own natural pivot. Its centre of mass.
This may look like an ordinary beach ball, but it's not. Watch how it moves.
It's hard to catch.
Why does this beach ball move in such a crazy manner?
This beach ball has its centre of mass located far from its geometrical centre. There's a container
over here on the side of the beach ball that's full of water so that most of the mass of the ball is
located here where I can touch. As a result, the centre of mass is here on the surface of the ball.
And when I throw the ball, and it becomes a falling object, it's that centre of mass that travels in the
arc of a falling object. The rest of the ball comes along for the ride. And it rotates about its centre of
mass, its natural pivot. And therefore about one surface, one side of the ball. So that wobbly
motion you're seeing is the ball rotating about the side of the ball, its natural pivot where the centre
of mass is located.
You can begin to locate a small object's centre of mass by setting it on a surface to support its weight
and then giving it a spin. It naturally spins about its centre of mass.
So, what I can say in, for this basketball is that the centre of mass of the basketball lies somewhere
on this rotational axis. It's spinning about a line, passing from top to bottom of the ball, and the
centre of mass is located on that line. I can't tell you for sure where along that line is unless I rotate
the ball and spin it again, rotate the ball and spin it again, but eventually, I could pin down the fact
that for a basketball, the centre of mass is pretty much dead centre in the geometrical centre.
That's true of a basketball. But not so true for knife.
How do you find the centre of mass of a knife?
Give it a spin.
It's right about there. It's somewhere, that's the point that's staying put as it spins. It's spinning
about that point. So I can tell you the centre of mass is somewhere ...between my two fingers.
To pin it down further, I'd have to spin the knife about another axis.
Can I do it?
Ooh. I can. So now I've really pinned down the centre of mass of the knife. It's really right there in
the middle of this metal piece.
Well, for a seesaw, you do the same thing. So here's a seesaw board. You give it a spin. The point
that's trying to stay put is right about here. So that's, that's the centre of mass. Somewhere
between my fingers. And that's where the pivot goes when you make the seesaw into a real
rideable seesaw.
And I can pull one of those up. Here it is.
The rideable seesaw if you're very, very small. Is supported right at its centre of mass, and therefore
pivots naturally about that point. So we're supporting it right at its centre of mass, and allowing it to
undergo rotational motion about its own natural pivot.
When examining rotational motion, it's technically necessary to specify the centre of rotation. That
is, the point about which all the physical quantities of rotational motion are defined. We're free to
choose that centre of rotation. But some choices are better than others.
For example, if I'm rotating like this and we want to describe my rotation as simply as possible using
the physical quantities of rotational motion, the most obvious choice for a centre of rotation about
which to build our language is my centre of mass, 'cause that's the point about which I'm pivoting.
So, in this case, we define the centre of rotation as located at my centre of mass.
So for example, my angle of velocity now is about 90 degrees per second up, remember the right
hand rule, about my centre of mass. So about my centre of mass, is pinning down the centre of
rotation about which our language is built. But if I'm rotating not about my centre of mass, but
about my thumb, watch this.
Here we go.
I can pivot about things other than my centre of mass. I need help to do that. But I can do it, and
I'm now pivoting about my thumb. So, it makes good sense to define that as our centre of rotation
and to say that I am currently rotating. My angular velocity is about 90 degrees again, up, about my
thumb. That's the centre of rotation.
Well, by now I hope you can see that while choosing a centre of rotation is necessary to define the
physical quantities of rotational motion, stating that centre of rotation explicitly every time you use
1 of those physical quantities is a nuisance, and I'm going to stop doing it. Instead I'm going to
assume that the centre rotation that we have in mind is obvious, unless it's not, in which case I will
say it.
So, for this case of a seesaw mounted with a pivot passing right through its centre mass, its own
natural pivot, that’s an obvious choice for our centre of rotation. Right here in the middle of the
board where the pivot passes through the centre of that board's centre mass. That's the obvious
choice for the centre of rotation. And we’ll assume for the remainder of this story, that every
physical quantity of rotation is defined about that point. So, instead of adding language now to all
our physical quantities of rotation for the seesaw, let's put some riders on it.
And that's the job for the next video.
Part 3.
Why does a lone seesaw rider plummet to the ground?
The answer to that question is that the lone rider produces a torque on the seesaw and causes it to
undergo angular acceleration. The seesaw rotates such that the rider descends toward the ground.
And hits it.
There are several ways of examining this situation. So I'm going to follow the path that I think is
most straightforward.
The rider's weight gives rise to a torque on the seesaw. And since the seesaw is no longer
rotationally inertial, its angular velocity is no longer constant. Instead, that angular velocity changes
with time, and the rider soon plummets to the ground.
But those observations give rise to two more questions.
How does the seesaw respond to torques, and what is the origin of this particular torque?
So let me start by looking at the seesaws response to torques.
When the seesaw is experiencing no outside torques it's covered by Newton's first law of rotational
motion. So it rotates at constant angular velocity, like this.
But once there is a torque acting on the seesaw, the seesaw is no longer covered by Newton's First
Law of Rotational Motion. And its angular velocity is no longer constant. Instead, its angular
velocity begins to change with time. The seesaw undergoes angular acceleration. Angular
acceleration is another vector physical quantity of rotational motion, and it is the rate at which
angular velocity is changing with time. Like ordinary acceleration, translational acceleration, it's a
subtle quantity. It's hard to see. You have to look carefully. It takes three glances to see
acceleration and it takes three glances to see angular acceleration. So I'm going to illustrate angular
acceleration with my body and hope that you can see it happening.
So here we go, let me start, motionless, rotationally motionless. That is my angular velocity is 0. If I
change my angular velocity, during the time over which that angular velocity's changing, I am
undergoing angular acceleration.
So here we go.
I'm going to undergo angular acceleration, and then I'm going to stop undergoing angular
acceleration, and watch what happens. Here goes the angular acceleration; it's going to be...
Up.
Right hand rule again. I'm going to rotate. Here we go.
Shoop.
Okay, I did it. It’s over. I am now coasting rotationally, at constant angular velocity. But when I first
got started I was undergoing angular acceleration. If I don't undergo angular acceleration again, I'm
going to keep spinning here forever, and this will make me very dizzy. So I'm going to undergo
angular acceleration downward in a moment.
Ready?
Get set, whoop, there I did it.
So during those two extended moments when I changed my angular velocity I did it by way of
angular acceleration.
I'll show it to you again. I'm going to do Angular acceleration upward for about a quarter of a second
and then, I'm going to do Angular acceleration downward for about a quarter of a second and come
to stop.
Ready?
There. Now, I'm coasting and now.
So, the angular acceleration portion of that situation was during the changes in my angular velocity.
Coming back to the seesaw then, the angular acceleration is absent now.
Ready, get set, there it is. There were a lot of angular accelerations there at the bottom, but they
initially kicked in, the first angular accelerations Kicked in when the rider got on the seesaw. Right
now.
So we see, a torque causes a seesaw to undergo an angular acceleration.
But what if there's more than one torque, acting on that seesaw at the same time?
In that case, those torques add together to become a net torque, and the net torque is what causes
the angular acceleration. So for example if I've got 2 riders hopping on to the seesaw at once, the
seesaw can't respond with several separate angular accelerations at the same time, it only has 1.
Instead it responds to the net torque, produced by those 2 riders.
Well, if net torque causes angular acceleration, the question comes up is, how much angular
acceleration?
It turns out that the seesaw's angular acceleration is proportional to the net torque acting on it. So
if a gently net torque acts on a seesaw. It undergoes a small angular acceleration. But if a large net
torque acts on the seesaw, it undergoes a large angular acceleration. But there's a second factor
involved in determining the seesaw's angular acceleration, the seesaw's rotational mass.
Rotational mass is the measure of an object's rotational inertia, its resistance to undergoing
angular acceleration. Now traditionally that physical quantity is called moment of inertia and it has
various complexities to it. They're beyond the, the scope of our little discussion here. Not relevant
really to seesaws. So rather than trying to have you remember a name like moment of inertia, with
its complexities, I'll make our lives simpler by simply calling it Rotational mass. That conveys the
characteristic that it's a mass like thing, it's a resistance to acceleration of some form. In this case,
rotational acceleration.
So, this seesaw has a certain rotational mass, a certain resistance to angular acceleration. So if I
exert a certain torque on it, it responds with a specific angular acceleration. And I go back to, to
putting a rider. So, my little rubber stopper rider is here. If I put a certain rider on this seesaw and
let it undergo angular acceleration, well, it undergoes rather rapid angular acceleration, and down
goes the rider.
But I can increase the rotational mass of this seesaw. By adding a second board. When I do this, I'm
increasing the rotational inertia of the seesaw. Try to glue it and tape it in place. And now, it's less
responsive to the same torques as before.
In this case, if I put 1 rider on, it undergoes angular acceleration, but not as much. Overall, the
seesaw's angular acceleration is proportional to the net torque acting on the seesaw. And also
inversely proportional to the seesaw's rotational mass.
Those two observations form the basis for Newton's Second Law of Rotational Motion, which
states that an object's angular acceleration is equal to the net torque acting on that object divided
by that object's rotational mass.
I'm going to ask a question about angular acceleration, but I'm going to do it in the context of a
bicycle wheel that I can hold in my hands. At present the bicycle wheel is motionless. And I'm going
to do three things to it, in sequence.
First, I'm going to start it spinning.
Second, I'm going to turn the wheel all the way around like this, so it's spinning in the opposite
direction.
And now as a third thing, I'm going to stop it from spinning.
The question is, during which of those 3 steps was the bicycle wheel undergoing non-zero angular
acceleration?
All three steps involved angular acceleration of the wheel. When I started it spinning it went from
having an angular velocity of zero to having an angular velocity toward you. Remember the right
hand rule here. When I pivoted it around like this, I reverse the direction of the wheel’s angular
velocity from toward you to toward me. That's angular acceleration. I had to make the wheel
undergo angular acceleration to reverse its direction of rotation. And finally, when I stop the wheel
from spinning, I take its angular velocity from towards me to zero.
So, all three steps require the wheel to undergo angular acceleration.
So, we see that a seesaw responds to a net torque by undergoing angular acceleration.
Why then does a low rider sitting at the end of the seesaw board exert a torque on that board?
After all, the rider has a weight, which is a force, and if I hold the seesaw in place now, the rider and
seesaw are pushing on each other with forces. The seesaw to support the rider's weight and the
rider pushing back on the seesaw in response.
It's all forces out here. Where does the torque come from?
Well it turns out that forces and torques are related and that a force can produce a torque and a
torque can produce a force.
To see how that all works, let's go experiment with a door....because doors are a wonderful example
of rotational motion and the use of a force to produce a torque.
So here I am outside the physics building, opening and closing doors in a light rain. The things we
do for science.
Doors are a nice example of rotational motion. After all, they don't go anywhere. They simply
rotate open and closed about their hinges. They have all of the characteristics we've come to expect
of rotating objects. They have angular positions, they have angular velocities, and they even have
angular accelerations.
But that brings us to the issue at hand, which is when you open a door you do it by exerting a force
on the door handle. And yet the door undergoes angular acceleration.
Well, angular accelerations are produced by torques, not by forces. So how is it that a force exerted
on the door handle produces a torque on the door?
To show you how that works, I first have to define a centre of rotation. Now, the obvious place to
put the centre of rotation is somewhere along the hinge line. Because that's the line about which all
the door's rotation occurs. But I have to be more specific than that. Because centre of rotation is
actually a point. Not a line. So I'm going to put the centre of rotation in line horizontally with the
door handle for reasons that we'll come to eventually. And that's going to be our centre rotation
right there on the hinge line aligned nicely with the door handle.
Having done that then, let's look at ways in which not to produce a torque about that centre
rotation, starting with a force. So these are all the unsuccessful ways to try to open a door, some of
which you may have encountered by accident.
So, first unsuccessful way to produce a torque, starting the force, is to push the door handle toward
the centre of rotation. So I'm pushing right at that centre of rotation.
No effect. I'm producing no torque.
How about reversing my force? Instead of pushing toward the centre of rotation, let me pull away
from the centre of rotation.
Also, no luck. Doesn't do anything.
So we see that pushing toward or away from the centre of rotation is unsuccessful. How about
pushing on the centre of rotation? Let me come over here to the centre of rotation and push right
on it. I'll try to pull right on it, all the kinds of forces, none of it works.
So you can't produce a torque by exerting your force toward, away from or on the centre of rotation.
Okay. Now it's time to be successful. We can only take so much frustration. So now, I'm going to
exert a force out here on the door handle, not toward or away from the centre of rotation, but at
right angles to a special line. It's actually a vector. It's called the lever arm. And this is what the
lever arm is. The lever arm is going to be the vector that extends from the centre of rotation to the
point at which I'm going to exert my force. Namely on the door handle.
So there is a vector that points along this line to this point here. It has a length of about 1 meter, like
that and its direction is exactly to your left. And I'm going to exert my force, not along that vector
or, you know, with it or against it, but at right angles to it, perpendicular to that lever arm. I'm going
to exert my force toward you, and watch what happens. The door undergoes angular acceleration
and begins to rotate open.
That is how to produce a torque starting with a force. If you exert your force at a lever arm, from
the centre rotation, that is the vector that extends from a centre of rotation to where you exert your
force. And you exert your force at perpendicular to that lever arm. Then you produce a torque.
And the torque has a specific direction. Its direction follows yet another right hand rule. If you take
your right hand and extend your index finger in the direction of the lever arm towards your left
right now. And then you sweep the index finger of your right hand in the direction of the force
which is towards you. So that's the sweep. Look what my thumb is doing. My thumb is pointing
up. That is the direction of the torque I produced in pulling toward you on the door handle.
The lever arm is that direction. The force is toward you. The torque I exert is up, and so it causes
upward angular acceleration in the door, which swings open.
Now the amount of that torque that I produce depends on two things.
One is how much force I exert. The torque is proportional to the force I exert. A gentle force
produces a gentle torque. A big force produces a big torque. So, that's the first observation.
Second observation is, the length of the lever arm matters. The torque I produce is proportional to
the length of that lever arm. Here I have a lever arm about that long, but if I go inside and I push
near the hinges, I can make the lever arm very short; and watch what happens.
That was hard.
So, I'm exerting my force here, very close to the pivot, therefore at a very short lever arm, and I'm
obtaining a very small torque until I really crank up my force.
We can combine these observations to relate the force to the torque it produces, quantitatively.
That torque is equal to the lever arm times the force. Where only the component of force that is
perpendicular to the lever arm is included. And where the torque is in the direction determined by
the right hand rule.
So in this case if the lever arm is pointing to your left and the force is pointing toward you, the
torque is up.
Now this door is complicated because it has a closing mechanism, like many doors. It has a system
to try and keep that door closed when you leave it alone. So it's not free to exhibit rotational inertia
and has all kinds of its own trouble and I had to overcome that resistance, that mechanism trying to
keep the door closed. That's a lot easier to overcome if I'm out here with a big lever arm. I can exert
relatively gentle force on the door handle and get the door to open despite the closing mechanism.
If I try to push very close to the hinges, that closing mechanism is hard to beat.
And you may have had this experience that if you go to a door that isn't very well labelled and you
have to push it open andyou can't tell which side of the door has the hinges. If you push near the
hinge side of the door, the door doesn't open very easily. It's very resistant to opening because
you're producing so little torque with your force. You need to go out to the other side of the door
where you have a big lever arm to work with and therefore can really create a lot of torque with a
small force.
To produce a torque with a force then, all we need is a lever arm.
For an unconstrained seesaw like this, one that can rotate in any possible direction, the options are
limitless.
I'm going to choose as our centre rotation the seesaw's centre of mass just for convenience here,
right about there. And now, let me show you a couple of torques. Things you've seen before,
maybe some you haven't.
If I come out here to a lever arm towards your left and then I push down with my force, which is at
right angles to that lever arm or, in fact I don't have to be perfectly right angles I have to just have to
have some component that's at right angles to the lever arm. And I push down, I cause an angular
acceleration toward you. Right hand rule again.
On the other hand, if I come out to a lever arm, same lever arm. But I push my force towards you.
Watch what happens. I cause angular acceleration up. And if I come out to a level arm toward you,
very short one but it's there, and push down, I caused angular acceleration to your right. I flipped
the board like that.
Well. This is exciting, but very complicated. There are too many options with our unconstrained
seesaw. So fortunately, we're going to focus on a constrained seesaw, one that has a pivot shot
through the centre that forces it to rotate in a very simple manner.
This seesaw board down here cannot do this kind of rotation, or this kind of rotation. And so, it
operates in a more simple fashion, like this.
And it still exhibits the same sorts of behaviours. To produce a torque on this seesaw, I come out to
a lever arm and push at right angles, or partly at right angles to that lever arm down and I cause
angular acceleration toward you. Because my torque was toward you.
We've seen how to produce torques with forces in the context of doors, in the context of seesaws.
But what about another important household use of torques, putting in or taking out screws or
bolts?
You rotate a bolt into place and you rotate it the other direction to take it out of place. Well
suppose you have a big bolt like this that has rusted in place, and you're trying to get it out but it
won't turn when you grab it with your hand and try to twist. You need more torque. So, in that case
you get a wrench.
This is a device, and you will have to figure out how it works. This is a device that when you put it on
the head of the bolt, it allows you to produce more torque. And by now, you should be thinking
about how this works.
But what if this is really, really stuck?
And you need a bigger wrench?
Well, that's already a pretty big wrench, you think. And you're probably thinking that I'm going to go
over and get this wrench. To show you the bigger wrench.
But no. I have in mind this wrench. And so we take this wrench, put it on our stuck bolt. And lo and
behold, it's a lot easier to produce a large torque on that bolt and remove it from wherever it's
stuck.
The question then, is this, why is using this larger wrench more effective? Why does it enable you
to remove that bolt when this wrench didn't to the job?
This wrench has a longer handle, and it provides a longer lever arm with which to produce a torque
using a force. So when you come out here to the end of the handle and push perpendicular to that
handle and therefore perpendicular to the lever arm, your force produces a larger torque as
compared to this wrench. There's just not as much length here to work with. It's got a shorter lever
arm and so when you push on the handle of this wrench with that shorter lever arm your force
produces less torque.
So we see, whenever a lone rider goes out to a lever arm on the seesaw and sits down, the rider's
weight gives rise to a torque on the seesaw that causes it to undergo angular acceleration, such that
the rider ends up pretty much sitting on the ground. The rider's weight is a force and that weight
causes the rider to push on the seesaw with a force, but the force acting at a lever arm from the
centre rotation produces the torque that causes all this to happen.
Pretty much the only place a single low rider can sit or stand and not produce a torque on the
seesaw is exactly on top of the pivot, which is kind of an interesting place to stand. And I must admit
to having done that myself, from time to time. But it's much more fun to have 2 riders on a seesaw,
and that is the subject for the next video.
Part 4.
Why do the riders' weights and positions affect the seesaw's motion?
The short answer to that question is that they affect the net torque on the seesaw, and therefore
the seesaw's angular acceleration. In most cases, the riders of a seesaw position themselves so the
net torque on the seesaw is 0 or very nearly 0. As a result, the angular acceleration of the seesaw is
either 0, that is, its coasting rotationally. Or it's just got the smallest amount of angular acceleration.
Well, that then requires a longer explanation.
How does that come about? You put riders on the seesaw; why don't they produce enormous net
torques?
So we know that if we put one rider on the seesaw, that rider, because of the rider's weight, the
rider pushes down on the seesaw over here, on your left... That's to the lever arm from the pivot. It
produces a torque and boom, the seesaw undergoes rapid angular acceleration such that, that rider
drops to the ground.
But what if we put two riders on the seesaw simultaneously?
And what I'm going to do is I'm going to position them very carefully.
And look. The seesaw is experiencing very little angular acceleration, so the net torque on it is either
zero or very near zero.
How did that happen? Aren't these riders producing big torques on the seesaw?
There are two of them.
Ahh! Glad you asked that question.
Here's the story, this is now the longer explanation to the question that's prompted this video.
That rider because the rider's weight is pushing down on the board, over here to your left, the lever
arm that, that rider’s force is using to produce a torque, points towards your left. Here it is, and
using the right hand rule now, we can see the direction of the torque produced by that rider. The
torque, we follow the lever arm and we roll, I roll my finger down in the direction of the force and
my thumb is pointing toward you. That is the direction of a torque, produced by this seesaw rider.
Let's come over to this seesaw rider. I need my right hand again. I can't swap hands or I'll get the
wrong answer. So, that rider by virtue of his or her weight, is pushing down on the seesaw board.
The lever arm with which that rider is producing a torque now, points to your right.
So, there it goes. And now I turn my index finger in the direction of the force. And lo and behold, the
torque produced by that rider is away from you. So these two torques are in opposite directions.
This rider is producing a torque toward you. This rider is producing a torque away from you.
When we add those two torques, and they are the two torques acting on this seesaw, they sum to
zero or very nearly zero. And that's how it is that when I let go of this board and allow it to show you
its angular acceleration there's almost zero. If there is a little bit, and there is, I can adjust the
distance of one of the riders from the pivot.
This riders producing a little too much torque. And now I, I move it toward the pivot, still a little too
much torque. So I move it a little closer to the pivot, and now that rider's producing almost just the
right torque. Let me move the rider in a little closer and now this rider's producing too little torque.
I have adjusted the rider's positions, that is the lever arms they're using, to show you that we can go
all the way from almost perfect balance, and I'll talk about balance in a minute, with that rider
dominating a little bit, to almost perfect balance with that rider dominating a little bit. And
everything in between, including in principle, perfect balance where there's zero net torque on the
seesaw.
Actually, balance is an interesting concept. The balance that we talk about in the context of a
seesaw, and many other objects that teeter back and forth like a seesaw, is a situation where
gravity produces no torque on the object. So, when this seesaw is balanced it's experiencing 0
torque due to gravity. I can come in and change things. I'm here, very carefully adjusting positions
in order to try get this situation.
This seesaw is almost perfectly balanced. Meaning it's experiencing almost 0 torque due to gravity.
And that is the normal situation for a seesaw, and riders, they like that situation because a balanced
seesaw is free of torque, this assumes nothing else is exerting torques on it, and it will turn at
constant angular velocity. It is an object that obeys Newton's First Law of Rotational Motion. And
it's not wobbling, it's rigid, assuming the riders don't change their positions.
And therefore, in the absence of any torque, and there's no gravitational torque on a balanced
seesaw, it turns a constant angular velocity. So, the reason the riders have to adjust their positions
very carefully and their weights are important as well, is because they are trying to sum their
torques to zero, and how they place themselves matters.
If, for example, the two riders have, essentially identical weights, and these two riders do, they need
to sit at equal distances from the pivot because the torque they produce, after all, is the product of
the force they exert on the seesaw times the lever arm they have to work with.
There's some subtleties in here with regard to the angles involved between the lever arm and the
force but in this situation we can really ignore those. The forces and lever arms are essentially at
right angles to each other, and our lives are simple.
So these two identical riders, seated at identical distances from the pivot, produce identical but
oppositely directed torques, and the seesaw balances.
What if we have a heavier rider around, though?
So instead of this rider, we bring up one. And this is made of steel. This is heavy stuff. So I'm going
to put this rider in.
If I put this rider out at the same distance as the rider on your right, it completely dominates, and I
run the risk of tossing this rider. This is one of the flaws with seesaws, it's easy for one of the riders
to become an astronaut, when a very heavy rider gets on the seesaw and does that to it.
But this rider cannot sit that far out from the pivot. Too much lever arm for a large force, and
therefore this rider dominates it, and produces a torque that, that one cannot compensate for. So I
have to bring the heavier rider in close.
How close? Pretty close.
I'm almost at balance. There we are, this is balance. Alright? It's as close as I'm going to get. And,
again, the net torque on the seesaw is zero, or pretty close to zero. And, you'll notice that now the
lever arm with which this rider is producing the torque, is quite short because this one weighs a lot,
so big downward force, short lever arm. And that is balancing, or cancelling out the torque due to
this one, which is in the opposite direction, but it's produced by a smaller force acting at a larger
lever arm.
So this is common in playing on a seesaw when you have two children of significantly different
weights. They have to sit at different distances from the pivot. The heavier child sits close to
produce a certain torque, and the lighter child sits far from the pivot to produce an equal amount of
torque but in the opposite direction.
Well, that brings us to a question. And the question is this.
Can two riders, and we can adjust their weights as you like, ever sit on the same side of the
seesaw, and still balance the seesaw?
Two riders cannot sit on the same side of the seesaw, and expect the seesaw to balance. That's
because those two riders produce torques in the same direction about the pivot. Their forces are in
the same direction, their lever arms are in the same direction, so their torques are in the same
direction. And when you add those torques, they sum to something larger than each one
individually. So you get a lot of torque on the see-saw, and it’s terribly unbalanced.
In order to balance the seesaw, the two riders, or however many you want to put on the seesaw,
have to distribute themselves on opposite sides of the pivot so that their torques cancel one another
and eventually, if you do it all right, they sum to zero and the seesaw is rotationally inertial. It has
zero net torque on it and no angular acceleration. It coasts rotationally.
There are two seemingly different ways to think about the balanced seesaw situation.
The first way is the way we've been doing. Where this rider produces a torque, that rider produces a
torque, the two torques sum to zero and as a result the seesaw experience zero torque due to
gravity. It's balanced.
The second way to think about this situation is in terms of a concept known as the centre of gravity.
Now centre of gravity is the effective location of an object's weight. I have one. You have one.
These riders have one. Even the seesaw board has one.
This rider's centre of gravity, that is where its effective weight is located, is pretty much at its centre.
Same with that rider. The seesaw board's centre of gravity, the effective location of its weight, is at
its middle. Right there. And that might make you think that centre of gravity, which is here, and
centre of mass, which is here, are the same idea.
Centre of mass, centre of gravity, aren't they the same?
They're not. They happen to coincide for all objects here near the earth's surface. Celestial objects
violate this concept for complicated reasons that I'll leave for another day. But small objects do
have their centres of gravity at the same locations as their centre of mass, but they're different
concepts.
Centre of mass is the effective location of an object's mass. It's natural pivot. We watched centres
of mass in action when I threw various wobbling objects or sticks and so on through the air and
you'd watch the centre of mass was traveling in the arc of a falling object. That's the mass moving
and the inertial properties of the object in play. So, centre of mass is all about inertia in motion.
Centre of gravity is about forces and it’s forces of gravity. It's got to do with gravity. If there's no
gravity around, centre of gravity means nothing. So it's the effected location object's weight.
The fact that weight is proportional to mass here near the earth's surface, means that centre of
gravity and centre of mass share the same location. But they're different concepts and so if you're
dealing with the inertial aspects of an object, you're probably paying attention to the centre of
Mass.
If you're dealing with the gravitational or weight aspect of an object, you're probably dealing with
centre of gravity.
So, back to the situation here.
We have objects with various centres of gravity and that brings us to an observation that this entire
structure, two riders on a seesaw is, we can consider it as a single object. Where is its centre of
gravity? That composite object.
And it turns out that this overall object's centre of gravity is located right above that Pivot. And it's
being pulled straight down, like the centres of gravity are pulled straight down. They're gravity after
all, right? The forces of gravity are toward the centre of the earth. It's being pulled straight down
right towards the pivot, the centre of rotation.
And as we've seen before, forces that act toward the centre of rotation produce no torque about
the centre of rotation. So, this seesaw is balanced in two ways you can think of it:
One is in terms of the individual riders producing torques that sum to zero.
The other way, which is kind of cool, is that the riders and seesaw together have a centre of gravity
located vertically above the pivot. And therefore, the force of gravity acting on this entire structure
acts right toward the pivot and produces no torque. It's along the lever arm and produces no
torque.
So Annie and Megan here are riding a real seesaw, not one of the little things I have in my lab. And
they’re balanced right now.
Can you show us this?
It takes delicate adjustment, but Megan's distance is just right from the pivot, the pivot's right here.
Annie’s distance is just right from the pivot, they've adjusted it, so the net torque on this thing is as
close to 0 basically, as they can get it. But this is a boring way to ride seesaws, if you just sit here
balancing.
I guess it's not too boring. It's kind of exciting, trying to keep it balanced. But they can unbalance it
in order to rock back and forth in one of two ways. They can either push on the ground with their
feet.
So, Meagan, why don't you push on the ground? Okay, and that extra force produces another
torque, which causes Annie to rotate down. Now Annie can push down on the ground and cause
Meagan to rotate down. So, they're causing angular accelerations back and forth by exerting new
torques on it.
The other way they can unbalance this is by leaning.
So each one of them has a centre of gravity that's located somewhere sort of mid-body. But if they
lean, they can shift the location of their centre of gravity and therefore exactly where they're
exerting the forces on the seesaw board, and cause it again to experience a net torque so it
undergoes angular acceleration.
So, if you both lean towards Annie, what happens?
It goes down, Annie goes down, because basically the lever arm with which she's working gets
longer. And the one that Megan's working with gets shorter. So the torque is this way, toward me.
But now if we lean, everybody lean towards Megan.
Now the lever arms get longer and shorter in the opposite direction, and the net torque is toward
you. So, they can rock back and forth, so, this is how a seesaw works.
Okay, you guys can go at it.
All right, here we go.
Either way.
And this is what makes seesaw fun right, is all the adjustments of the torque so that you undergo
angular acceleration in opposite directions, back and forth.
>> This is so funny!
>> Seesaws are not the only structures in our world that need to balance. Mobile sculptures do as
well.
This mobile sculpture is entitled, happy hanging hardware. And I built it out of a torque wrench, a
ball peen hammer, and a metal file.
Amazingly enough, each of these components is rotationally inertial. You don't see any of them
undergoing angular acceleration, after all.
And that brings us to a question.
For all of the components of a mobile structure, to be rotationally inertial, how must those
components be arranged?
Each component of this mobile structure has its centre of gravity at or below the point at which that
component is supported. In effect, the pivot, about which that component could rotate.
This is actually a relatively complicated concept though. Because there are three components here
which aren't the individual tools.
First component, the simplest, is the file. That file has its centre of gravity at or below this support
point. Which is the loop of string going around it. That's the pivot about which the file can rotate.
And so, the file has its centre or gravity at or below that pivot. And therefore gravity produces no
torque on the file, it's rotationally inertial.
So far, so good.
The ball peen hammer isn't an object by itself, it's not the component by itself. Rather, the ball peen
hammer and the file together are the next component of this mobile. And that combined object,
ball peen hammer and file has its overall centre of gravity at or below its support point. This loop of
string.
And lastly, the torque wrench and everything below it has its combined centre of gravity at or below
this support point. The support point that is acting on the torque wrench.
So, each of these components, the file and the hammer and file and the wrench, hammer and file,
each of those components has its centre of gravity directly below its support. And therefore, gravity
and pulling down on the centre of gravity produces no torque on that component about its pivot. It
doesn't undergo any angular acceleration then due to gravity, it's balanced.
And so the file is balanced. The hammer and file are balanced. The wrench, hammer, and file are
balanced. The entire mobile then, is balanced, and it's all rotationally inertial.
So we see that objects that can rock or tip are only rotationally inertial if you balance them carefully.
Sometimes that's what you want, like with a mobile. Sometimes that's almost what you want, like
with a seesaw, where getting it perfectly balanced is interesting, but kind of unexciting in the long
run and you want to unbalance it a little bit to get some action happening.
We'll talk more about balance in the episode on bicycles, but for now, it's clear that in the context of
seesaws, balance and near balance are the name of the game.
Part 5.
Why do the riders' distances from the pivot affect the seesaw's responsiveness?
The answer to that question is that the farther the riders’ masses are from the pivot, the greater the
seesaw's overall rotational mass and the slower its angular accelerations.
Two riders can balance the seesaw in a variety of ways.
To begin with, they can go to the ends of the board and adjust their distances from the pivot
carefully until it balances. That is, until it experiences zero overall torque due to gravity. I mean I'm
pretty much there. Balanced seesaw.
But they can also come in close to the pivot and sit like this, with much smaller lever arms to work
with now, so that they're producing much smaller torques as individuals. But once again, those two
torques sum to zero. And there's zero overall torque due to gravity on this seesaw.
So, there are a variety of ways to balance the seesaw. And you might think that there's no
significant difference between those choices, but that's not true, there is a significant difference.
The farther these two riders sit from that central pivot, and therefore the axis of rotation, the
greater the seesaw's overall rotational mass. Now, rotational mass is not something completely
independent of ordinary mass. They're related, just as forces and torques are related. Every portion
of the seesaw's ordinary mass contributes to the seesaw's rotational mass. And the amount of
that contribution depends on where the portion of ordinary mass is. More specifically, on how far
that portion of ordinary mass is from the axis of rotation.
And that dependence on axis of rotation is a strong one. Small, modest changes in distance from
the axis of rotation can lead to large changes in the rotational mass contribution. The amount of
rotational mass contributed by a portion of ordinary mass is equal to the ordinary mass itself
times the square of the distance between that portion of ordinary mass and the axis of rotation.
So, taking a small portion here and doubling its distance from the axis of rotation doesn't just
double its contribution to the rotational mass, it quadruples it. That means that for the riders,
when they sit in close, and their distance from that central pivot and centre of rotation, axis of
rotation, is small, they contribute very little to its rotational mass, the overall rotational mass of the
seesaw and riders.
Even though these, these riders have large masses, they're too close to the axis of rotation to
contribute very strongly to its rotational mass. But if they go out like this, to a large distance, well,
then their contribution to rotational mass is huge. They might be only ten times as far away from
the pivot as before. From that axis of rotation. But an increase of distance by a factor of ten is an
increase in contribution to rotational mass of ten times ten, or ten squared, which is 100. So the
rotational mass contribution of these riders could easily be 100 times that of these riders.
It's a big effect. To see how big, I've made these two rods that look the same, and have the same
the masses. They contain the same materials actually. But the difference is that in one of these rods,
the mass is all in the middle, near my hand, under my hand, hidden from view. And in the other bar,
all of the mass is far from my hand, at the ends of the bar.
So, same mass, but in this case it's moved way out far from the centre of rotation, which will be here
in the middle bar. And the rotational mass of this bar is something like 30, 40 times that of this one.
Big difference. To see that difference, since you can't hold the bars, let's go get some help.
Annie and Megan are going to help me here with these two bars.
Now, these bars have the same masses and the same weights. So you could check that out. Just,
just compare the weights, do they feel the same?
>> Yeah, definitely even, uh-hm.
>> Yeah, definitely.
>> So, just by weighing them in your hands you can't tell the difference between these two bars. But
that doesn't mean they're identical. So the difference is going to be subtle, and this difference will
show up maybe when you begin to try to rock them back and forth.
So I want, Annie grab it in the middle of the bar, Megan same thing.
And I'm going to count to three, and on the number three, I want the two of you to rock it back and
forth as fast as you can. That is, make it undergo angular acceleration first one way and then the
other, back and forth as fast as you can.
>> Uh-hm.
>> 'Kay.
>> One. Two. Three.
>> This is really difficult.
>> So Annie's having no trouble here, and Meagan's really lagging behind. Must be weak today,
right? Forgot to eat your breakfast.
Okay, now swap bars.
>> Okay.
>> Thank you.
>> Now, I'll count again. One, two, three.
>> Oh.
>> Miraculous change.
>> What?
>> Something's different about these two bars. What do you think's different about the bars?
They have the same mass, what's different?
Megan?
>> Maybe the distribution of the mass within the bar?
>> So the distribution of the mass within the bar is different. Where is the mass in your bar, right
now?
>> In the centre.
>> So your bar has almost all of the mass in your hand.
>> Yeah.
>> As a result, the moment of inertia, or the rotational mass of this bar is very small.
>> Yeah.
>> It's very easy to make this bar undergo angular acceleration.
How about yours, Annie. Where do you think the mass is located?
>> I mean they must be at the end, right?
>> Yeah, so all the mass in this bar is at the ends where it contributes enormously to rotational mass.
So they have the same mass, it's just distributed differently. In Annie's bar it's at the ends, in
Megan's bar it's in the middle. And they behave totally differently when you try to rock them back
and forth.
>> Uh-hm.
>> Show us a little more time.
>> Sure.
>> I should make a face.
>> Yeah, it's, it's a pretty dramatic difference. Unfortunately you guys can't try it out.
>> But, but if you ever come by, test out these bars and see how different they are.
>> Okay.
>> Thanks.
>> Sure.
>> So you see, if you place an object's ordinary mass far from its axis of rotation, that object can
have a surprisingly large rotational mass. Now, the distance involved here is between ordinary mass
and the rotational axis. And you're often free to choose an object's rotational axis. If you do that,
and if you change your choice, you may well change the object's rotational mass. That ability to
change an object's rotational mass is why rotational motion is so complicated to calculate
quantitatively.
And that's a fact the keeps first year physics graduate students rather busy. It's hard work. I want to
give you a taste of the issues without trying to overwhelm you with them.
But look at this rod. This is the rod that's very hard to wobble back and forth like this because it has
an enormous rotational mass when you twist it back and forth about this axis. The one pointing
toward you through my hand or away from you through my hand. About that axis, gigantic
rotational mass.
But what about this axis in which I'm twisting it back and forth like a drill or a screwdriver? It's
easy. This direction has almost no rotational mass. That's because all the portions of ordinary mass
are very close to this spindle-like axis about which I'm twisting it.
So, this rod here, has two very different rotational masses, a huge one when you do this motion and
a tiny one when you do this motion.
Now this is, a, you know, fun and games rod. But something you're more familiar with is perhaps a
tennis racket. The tennis racket is a classic example of something that has three particularly
important rotational masses.
Its smallest rotational mass is for this rotation about the top bottom axis right now. This motion,
most of the mass is pretty close to that axis, the spindle about which I'm twisting it, and therefore it
has a relatively small rotational mass.
The next larger rotational mass is for this motion. Sometimes referred to as the frying pan motion,
when you're, you're flipping pancakes. So this is the intermediate rotational mass.
And the biggest rotational mass is for this rotation.
In between these motions, life is extremely complicated. And it's beyond the scope of this class as
something I don't like to deal with anymore. I've done it. Been there, done that, I'll leave it.
But these three distinct rotational masses, this small one, bigger one, biggest one, give the motion of
a tennis racket or anything shaped like a tennis racket, the rotational motion's quite complicated.
To make things even worse, these are all motions about the centre of mass. These are all rotations
in which the centre of mass stays put.
What if you shift the rotation, so that you don't care about the centre of mass of the tennis racket?
For example, when you're swinging a tennis racket about your shoulder. In that case, you're shifting
the mass of the tennis racket even farther from the centre of rotation, the axis about which you're
spinning it, and creating an even larger rotational mass for the tennis racket.
So the bottom line with all of this is rotational mass depends on your choice of axis of rotation.
We're finally ready for the question I asked you to think about in the introduction of this episode. To
remind you, that question asked if you and a child half your height lean out over a swimming pool
at the same angle and let go at the same moment, which of the two of you will hit the water first?
Despite a fair amount of rotational physics under our belts, that remains a challenging question.
So before I ask it, and leave you free to answer it, I want to give you a little more background. Get
you all prepped for this question.
First, what's the big picture issue? What is going to determine who hits first?
It's going to be angular acceleration. The one of you that undergoes the fastest angular acceleration
will develop the fastest angular velocity, will tip over the fastest and will hit the water first. So look
for big angular acceleration.
Second, what is the axis of rotation about which the two of you are going to be rotating?
It's not your centres of mass, it's going to be here at your feet.
That leaves two more issues. One is the cause of angular acceleration and the other is the
resistance to angular acceleration.
The cause is the neck torque on you. The resistance is your rotational mass.
And let's look at each one individually.
First Torque. The torque is due to gravity, and to make our lives simple, let's compare the torques
about this, about your feet, that's the axis rotation here for you and the child. Now, I've made life
very simple by using exactly the same board material. One is just half as long as the other, and this
makes, you know, this has all the physics in it, but none of the details. Life is easier.
So, you have twice the weight of the child, that's no surprise. And that weight effectively acts at
your centre of gravity, which is twice as far, it's right here in the middle. It’s twice as far from the
axis of rotation, as for the child. So, you're experiencing four times the gravitational torque of the
child. You have twice the weight acting at twice the lever arm. 2 times 2 is 4.
Right? 4 times the torque. That's the cause of angular acceleration.
How about the resistance to angular acceleration, the rotational mass?
Well, as compared to the child who has half the mass here, distributed around here with the centre
of mass being about there. You have twice the mass distributed here and there's a centre of mass
here. The centre of mass has moved out by a factor of two. You have twice as much mass, that is on
average at twice the distance from the axis of rotation, namely your feet.
Well, remember that the distance involved here in calculating it, the contribution of mass depends,
not on distance, but on distance squared. So the rotational mass that you have is eight times that of
the child. Twice as much mass, at twice the distance and you square the distance. So it's two times
two times two, that's eight. You have eight times the rotational mass of the child.
With that as background now, answer the question.
Which of the two of you tips over fastest and hits the water first?
The child undergoes greater angular acceleration, develops a bigger angular velocity and hits the
water first.
If you haven't already tried this experimentally, give it a go. All you need is two sticks, one twice as
long as the other. I can show you what you'll see when you try it.
Here's you, here's the child, and we'll put you both on your feet and tip you to the same angle, and
then let go. 3, 2, 1. No question, the child reached the water first. It's a battle between torque and
rotational mass. In both cases about your feet. You have four times the gravitational torque acting
on you as, as the child has. So there's four times as much twist trying to propel angular acceleration
but you have eight times the rotational mass of the child, resisting that angular acceleration.
Four times more impetus. Eight times more resistance, you get only half the angular acceleration of
the child.
So, the child undergoes twice your angular acceleration and just goes through the whole rotational
motion faster. And wins the race to the water.
Rotational motion clearly has some subtle complications, like a single object having more than one
rotational mass depending on your choice of axis of rotation.
But let's leave all those complications for the experts. I chose seesaws as the topic for this episode
because seesaws are comparatively simple. That pivot fixes the axis of rotation so that the seesaw
can only rotate in one fashion. And in general, it only has one rotational mass. Things are simple.
Nonetheless, the seesaw exhibits most of the issues of rotational motion. Or at least the ones that I
want to talk about and try to convey to you.
I've already done that now. I've shown you most of what happens in a rotating system like a seesaw
with one important exception.
Energy.
As the seesaw rotates, the riders are exchanging energy.
And that, is the topic for the next video.
Part 6.
How do the seesaw's riders affect one another?
The answer to that question is that they support one another and they exchange energy as the
seesaw rotates back and forth.
Let's start with the support issue. And to do this, I'm going to treat the seesaw as a facilitator rather
than the object of our main attention.
I'm going to define the centre of rotation as lying in the middle of the pivot. So the axis of rotation
for this entire story is right here at the pivot of the seesaw. But, otherwise, the seesaw is just
helping the red rider exert a torque on the purple rider about the pivot. And the purple rider exert a
torque on the red rider about the pivot.
Well, you might wonder why the red rider should ever care about exerting a torque on the purple
rider. That's because, the purple rider is already experiencing a second torque, a torque due to
gravity. Gravity is pulling downward on that purple rider, at a level arm from the pivot, the axle
rotation. So gravity by itself is exerting a torque on the purple rider, and that torque is towards me,
that is away from you.
To keep that purple rider from undergoing angle acceleration and plummeting toward the ground,
the red rider comes to the rescue.
Okay?
The red rider is exerting a second torque on the purple rider, and that torque is toward you. So the
second torque acting on the purple rider cancels gravity's torque on the purple rider. This is all
about that pivot, and prevents the purple rider from undergoing angular acceleration.
Uh-huh.
The red rider really is supporting the purple rider.
How about the other way around?
Well, the red rider is also experiencing a gravitational torque, forces down, lever arm is toward your
left. So, the gravitational torque on the red rider is toward you.
By itself, that would cause the poor red rider to undergo angular acceleration, boom, and drop
toward the ground. But once again, the purple rider comes to the rescue. And now, the purple rider
is exerting a torque on the red rider, that is, this way, toward me it cancels the gravitational torque
on the red rider and saves the red rider.
So the long and short of it is, the red rider is keeping gravity from twisting the poor purple rider to
the ground and the purple rider is stopping gravity from twisting the poor red rider to the ground.
They really are supporting one another.
So we have two torques between the riders. The red rider is exerting a torque on the red rider and
the purple rider is exerting a torque on the red rider.
How do those two torques compare?
They turn out to be exactly equal in amount, but opposite in direction. That's an example of
Newton's third law of rotational motion, which observes that for every torque one object exerts on
a second object, the second object exerts an equal, but oppositely directed torque back on the
first object. That's how our universe works again, it's never violated, it's always there.
So the red rider, when it exerts a torque on the purple rider, causes the purple rider to exert an
equal, but oppositely directed torque back on the red rider every time. And that ultimately allows
this whole thing to balance smoothly.
At the same time, the purple rider rescues the red rider from the grips of gravity. The red rider
rescues the purple rider from the same clutches, and so the two objects here both reach the
balanced condition at the same time. They all end up with no overall torque due to gravity.
This mutual support idea still works when one of the riders weighs far more than the other. If I
replace the red rider with this silver one, I can't put that heavy silver rider all the way at the end of
the board. I have to come in close to balance the seesaw, so right about here. And look what has
happened. That rider weighs far more than the red rider did, so, if I put it out far, it would produce
way too much torque to support the purple rider. It would turn the purple rider into an astronaut.
So, by pulling the silver rider in closer to the pivot, I have compensated for the silver rider's greater
weight by shrinking the lever arm that the silver rider uses to produce a torque about the pivot.
As result, the silver rider is still just perfectly supporting the purple rider against the purple rider's
gravitational torque. So, that part of the balance still works.
How about the purple rider's support of the silver rider?
Well, it still works there too. The gravitational torque acting on this silver rider was reduced by
bringing the silver rider in close to the pivot. Gravity is pulling down with a big force on that heavy
silver rider, but since that force has only a short level arm with which to work, it doesn't produce all
that much torque on the silver rider, about the pivot. As a result, the purple rider is still able to
support the silver rider. The silver rider may be heavier, but because the silver rider is closer to the
pivot, it doesn't take as much torque to support this silver rider against the torque produced by
gravity itself.
I haven't talked about units in rotational motion, because they're somewhat complicated and they'll
distract us from more important issues. But let me take a moment to mention the units of torque.
In the SI or metric system, the unit of torque is the newton meter. And it corresponds to a force of 1
newton exerted at a lever arm of 1 meter from the centre of rotation.
In the English system of units, the unit of torque is the foot pound. It corresponds to a pound force,
exerted one foot from the centre rotation.
I introduced the units of torque in part so that I can ask a question.
Here is a wood screw and I will screw it into the wood by exerting a torque on it, using my right
hand, that is down towards the wood. And now, I will unscrew the screw by exerting a torque on it
that is up out of the wood. If in both cases, inward torque and outward torque, I exert a torque in
the amount of 1 newton meter.
What torque does the wood screw exert back on me?
If I exert a torque of 1 newton meter on the wood screw, it has to exert a torque of 1 newton meter
back on me in the opposite direction.
That's Newton's third law of rotational motion. So as I exert a torque of 1 newton meter downward
into the wood block, it exerts a torque of 1 newton meter up out of the wood block on me. And if I
exert a torque of 1 newton meter out of the block, upward, on the wood screw, it exerts a torque of
1 newton meter downward on me, every time.
Now, let's watch the riders exchange energy as the seesaw rotates.
I've pretty well balanced the board here, I have the red and purple riders at about the right
differences from the pivot, so that the seesaw balances. It experiences zero net torque and
therefore rotates at constant angular velocity.
I'm going to hold the riders in place, so that as the seesaw rotates, they don't slide about and
possibly fall to the floor.
But what I want you to do is watch the altitudes of the two riders.
I'm going to make the seesaw rotate at a constant angular velocity toward you, that is, like this, and
the red rider descends as the purple rider rises. That means the red rider's gravitational potential
energy is decreasing, while the purple rider's gravitational potential energy is increasing.
Where did the energy from the red rider go and what provided the energy to the purple rider?
What a mystery.
Hm, I wonder.
As you might suspect, the red rider is transferring energy to the purple rider by way of the seesaw.
There are number of ways of following that energy transfer, so I'm going to pick what I think is the
most straightforward path. It involves the work that the red rider does on the seesaw and the work
the seesaw does on the purple rider.
I'm going to make the seesaw rotate very slowly at constant angular velocity toward you, and as I do,
I'll tell you how the transfer is occurring. Let me get it started here.
Okay, it's started.
We're going very slowly so I have time to talk. The red rider is pushing down on the seesaw as the
seesaw moves down in the direction of that downward force. So the red rider is doing work on the
seesaw. At the same time, the seesaw is pushing up on the purple rider and the purple rider is
moving up in the direction of that upward force. So the seesaw is doing work on the purple rider.
The job is complete, the red rider is transferring energy away to the seesaw and the seesaw is
transferring energy away to the purple rider.
Hope you could follow that. So, energy is flowing through the seesaw from the red rider to the
purple rider, pretty neat.
As the rotation occurs in the opposite direction, so I'm going to make it rotate a constant angle
velocity toward me, in this case, the purple rider's pushing down on the board as the board moves in
the direction of that push. Therefore, the purple rider is doing work on the seesaw, the seesaw is
pushing up on the red rider, as the red rider moves up in the direction of the seesaw's push. So, the
seesaw is doing work on the red rider. Again, energy is going from the purple rider into the board
and from the board into the red rider.
Because the seesaw is balanced, all of the gravitational potential energy lost by the rider that's
moving downward becomes gravitational potential energy in the rider that's moving upward. The
transfer of gravitational potential energy to gravitational potential energy is perfect.
If the seesaw isn't balanced, well then, it undergoes various types of accelerations and kinetic energy
becomes part of the equation. But this arrangement where a balanced seesaw is transferring
energy, and particularly gravitational potential energy, from the descending to the rising rider works
even if the riders have different weights.
If I replace the red rider with the much heavier silver rider and balance the seesaw again, I achieve
that balance by putting the heavier silver rider close to the pivot. Now, it's pretty well balanced. As
the seesaw rotates, at constant angle velocity which is what it normally does, the silver rider who is
close to the pivot, doesn't move up or down very much anymore. Right, they're close to the pivot.
They only move up and down, oh, no, this far, as the purple rider is moving up and down, you know,
much farther, more than a hand-width.
Wooh, that is the secret or maybe the explanation, behind the perfect transfers of energy again. If I
again rotate this balanced seesaw, at constant angular velocity toward you, the silver rider is
descending. It's pushing down on the seesaw board with a large force, because it weighs a lot. But
that seesaw that it's touching isn't moving very far. A little bit, but not all that far. So it's doing work
of a reasonable amount on the seesaw. At the same time, the seesaw is pushing up on the purple
rider with a more gentle force. But the purple rider is moving a longer distance. So the work the
seesaw is doing on the purple rider is the same as the work the silver rider is doing on the seesaw.
To make sure that's clear again: The silver rider is exerting a large downward force on the seesaw as
the seesaw is descending a short distance. At the same time, the seesaw is exerting a small, upward
force on the purple rider as the purple rider moves upward a large distance. The product of force
times distance travelled in the direction of that force, the products are the same. The work done by
the descending silver rider on the seesaw is the same as the work done by the seesaw on the rising
purple rider. Energy is transferred perfectly.
This arrangement of the seesaw, where a heavy rider can lift a light rider or a light rider can lift a
heavy rider, highlights the fact that the seesaw is an example of a lever. One of the simple
machines. Like all simple machines, the lever allows you to change the amount and or direction of
the force you're using to perform a particular task.
To make that clearer in this case, let me get rid of one riders, purple rider take a rest, and now, I'm
going to lift the heavy rider with my hand by exerting a force directly on the seesaw.
I can lift the heavy rider. And, in this case, the force that I'm exerting on this side of the seesaw was
relatively small much less in amount than the weight of the heavy rider. But as I lift the heavy rider, I
have to move the seesaw I'm pushing on much farther than the seesaw moves the heavy rider.
So I'm doing work as I push down on my side of the seesaw. And I'm doing it by exerting a small
force over a large distance. Whereas, the seesaw is doing work on a heavy rider consisting of a large
upward force exerted as the heavy rider moves a short distance. So, the work I do on the seesaw is
the same as the work the seesaw does on the heavy rider. But the relationship of force and distance
has changed.
And that's typical of many levers in our world, which brings me again to a question.
Let me get out a familiar lever and ask you about it.
It's an all too familiar situation. You take a nail, you pound it into a piece of wood. And then you
change your mind and you want to take the nail back out. So you grab the nail with your hand, you
pull as hard as you can.
No luck. Can't get that nail out. What are you going to do?
You take a claw hammer. That is, a hammer that has a groove in it, meant for grabbing the heads of
nails. And you grab the head of the nail with that groove. Tip the hammer and it plucks the nail
right out of the wood.
So the question is this, what aspect of what I did to the hammer is the same as what the hammer
did to the nail?
The hammer acts as a lever. And the work I did on my part of the hammer was the same as the work
the claw did on the nail, as the whole system rotated about an effective pivot where the top of the
hammer touched the wood.
So I was doing my work with a small force exerted over a long distance as the claw was doing its
work with a large force exerted over a small distance. This is why I was able to pull out the nail. It
was stuck tight and it needed a huge force to pluck it out of the wood. I couldn't provide that big
force with my own hands directly. But with the help of the hammer, I could pull it off, because I
have mechanical advantage associated with this lever.
I'm moving the lever far from the pivot, so I can use a gentle force and it's moving the nail close to
the pivot, so it provides a huge force. I don't get something for nothing, though. I have to exert my
force over a long distance, whereas the claw exerts its force over a short distance. Nonetheless, the
mechanical advantage provided by this lever allowed me to do something I couldn't normally do,
namely pull a nail out of a piece of wood.
As you can see, the rider's interaction on the seesaw is pretty sophisticated. Not only are they
supporting one another, but they're exchanging energy as the seesaw tips back and forth.
The seesaw is just a kid's toy, and yet, it exhibits all this really amazing rotational behaviour and in
particular, it acts as a lever allowing one rider to lift the other rider, allowing a heavy rider to lift a
light rider and a light rider to.
Wow, pretty much something for everybody.
Summary
A seesaw is a pretty amazing toy and a beautiful example of rotational motion. It rotates about its
own centre of mass, its own natural pivot so that, the only reason I need this physical pivot passing
through it is to prevent the seesaw from falling. If I could turn off gravity, I wouldn't need that
physical pivot to make the seesaw do exactly what it's doing.
Well, there is gravity so you need the central pivot. And the pivot also constrains the seesaw so it
can't do rotations that we don't want. It can only do what you see it doing at the moment. Although
it can also do that in the other direction.
The seesaw is balanced as well, meaning that it's experiencing no torque due to gravity. That's
because the centre of gravity of the seesaw is located right at the pivot as well. Basically vertically in
line with the pivot. In fact it's on the pivot. And as a result, the force of gravity produces no torque
on the seesaw about its pivot. No torques.
So, the seesaw is turning according to Newton's First Law of Rotational Motion. It's a rigid object
that is not wobbling. And it's not experiencing any external torques. So, it rotates at constant
angular velocity.
Well, when you put riders on the seesaw, life can get more complicated, which we've seen. Those
riders produce their own torques on the seesaw, and they move in various interesting ways. If
they're not balanced, the seesaw undergoes angular acceleration in various ways. But once they are
balanced, and again there is no gravitational torque on the seesaw and its riders, the seesaw is once
again rotationally inertial. It turns according to Newton's first law of rotational motion.
If they come out of balance and the seesaw undergoes angular acceleration, it does so according
to Newton's second law of rotational motion. The angular acceleration of the seesaw is equal to
the net torque acting on the seesaw, divided by its rotational mass.
And depending on where the riders sit on the seesaw, they can go from giving the seesaw a small
rotational mass to giving it a large rotational mass. Lots of flexibility. And as they're tipping back
and forth, they're exerting torques on one another, these two riders. And that's according to
Newton's Third Law of Rotational Motion. If the red rider exerts a torque on the purple rider, the
purple rider has to exert an equal but oppositely directed torque back on the red rider, every time.
And as they tip up and down, they do work on each other. They transfer energy to each other with
the help of the seesaw board. So there's really a lot going on here in the seesaw.
And we'll use many of these same concepts later on as we continue to look at how things work.