Download Basic Linear Amplifiers - benchmark

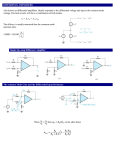
Chapter 2
Basic Linear Amplifier Circuits
INTRODUCTION
With this chapter, we begin the discussion of the basic
op-amp that forms the cornerstone for linear applications;
that is, the signal is directly proportional to the input signal.
Chapter 2
Basic Linear Amplifier Circuits
OBJECTIVES
At the completion of this chapter, you will be able to do the
following
Design, compare, and predict the performance of the following
op-amp circuits:
non-inverting amplifier
inverting amplifier
voltage follower
summing amplifier
difference amplifier
Chapter 2
Basic Linear Amplifier Circuits
OBJECTIVES cont.
Minimize the output-offset voltage due to the input bias current,
input offset current, and input offset voltage.
Recognize the input and feedback elements of linear op-amp
circuits.
Determine the effects of feedback upon circuit performance.
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
As shown in Fig. 2-1, the op-amp is connected as a non-inverting
amplifier. This is because the input signal is applied to the op-amp’s
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
Non-inverting (+) input. Resistor R1 is called the input element, and resistor
R2 is called the feedback element, since it diverts, or “feeds back” part of the
output voltage to one of the op-amp’s inputs. In this case, part of the output is
returned to the inverting (-) input.
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
For this non-inverting amplifier, the output voltage is given by:
 R 
Vo  1  2 V1
 R1 
(Eq. 2-1)
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
The voltage gain, or the ratio of the output voltage to the input voltage, is:
Voltage gain = Vo =
R
1 2
Vi
R1
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
Consequently, the voltage gain of a non-inverting amplifier will always be
greater than unity (1.0), no matter how large we make R1.
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
Since the input signal is applied to the op-amp’s non-inverting input, the
output voltage will always be in phase with the input.
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
More simply, when the input voltage goes positive, the output does the same.
The only difference between the input and output voltages is that the output
voltage will be I + R2/R1 times larger than the input.
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
As pointed out in the previous chapter, the open-loop gain AOL is an intrinsic
characteristic of the op-amp when there is no feedback.
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
When feedback is used, we then refer to the closed-loop gain ACL, Which is
simply the voltage gain of the op-amp configuration (Equation 2-2), or
for the non-inverting amplifier
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
The loop gain, AL is the reduction of the open-loop gain by the closed-loop
gain, so that by definition,
or
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
For all practical purposes, the input impedance of the non-inverting amplifier
is the intrinsic input impedance of the op-amp itself, which is high enough to
minimize loading of the input circuitry.
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
On the other hand, the output impedance of the circuit of Fig. 2-1 is
determined from the formula:
or
where Zoi is the intrinsic output impedance of the op-amp, as determined from
the manufacturer’s data sheet.
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
Example
To see how these concepts just discussed fit into place, assume that a type
741 op-amp is used in the circuit of Fig. 2-1 with R1 = 1 KOhm and R2= 100
KOhm
From Equation 2-3, the voltage, or closed-loop gain (ACL) is:
R
100k
ACL  1  2
 1
 101
R1
1k
From a given manufacturer’s data sheet, the open loop gain for the 741 op-amp is
typically 200,000. From Equation 2-4, the circuit’s loop gain (AL) is then:
AL= 200 000
101
= 2000
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
Example
Using a typical value of 75 Ohm for the 741’s intrinsic output impedance (Zoi),
the output impedance of the completed non-inverting amplifier is then:
Zo = Zoi/AOL
= 75 Ohm
2000
= 0.04 Ohm
From this example it should now be evident that the result of adding feedback
increases the loop gain, which in turn decreases the output impedance of the
amplifier circuit! We can then connect almost any load to the output, as long as
the maximum output current rating of the op-amp is not exceeded.
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
Usually, the calculation of the op-amp circuit’s output impedance can be
ignored since it is such a small number. It was included here to demonstrate the
effect of external feedback.
Chapter 2
Basic Linear Amplifier Circuits
Non-lnverting Amplifiers
End of Non-Inverting Amplifiers
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers
As shown in Fig. 2-2, the op-amp is connected as an inverting amplifier. This
is because the input signal is applied to the op-amp’s inverting (-) input
through R1, which is called the input element. Resistor R2 is the feedback
element. For the inverting amplifier, the output voltage is given by the equation
R 
Vo    2 V1
 R1 
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers
The minus (-) sign in the above equation indicates that when the input signal
voltage goes positive, the output voltage goes negative, and vice versa. In
other words, the output signal is of opposite polarity with respect to the input,
which is the same as saying that the output is 180 degrees out of phase with
the input.
 R2 
Vo    V1
 R1 
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers
The voltage, or closed-loop gain, is then:
Vo  R2 
ACL    
Vi  R1 
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers
Consequently, the voltage gain of the inverting amplifier can be either less
than, equal to, or greater than 1, depending on the relation of R2 to R1.
Vo  R2 
ACL    
Vi  R1 
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers
The loop gain is then:
AOL
 R1 
AL 
 AOL  
ACL
 R2 
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers
Unlike the non-inverting amplifier, the input impedance of the inverting
amplifier circuit is simply the value of the input element, R1, and will be much
less than that of the non-inverting circuit. The circuit’s output impedance, as
before, is determined solely by the op amps intrinsic output impedance and
the circuit’s loop gain, so that:
Z Oi
 R2 
ZL 
 Z oi 

AL
 AOL R1 
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers
For the special case when R1 and R2 are equal, we then have a unity gain
inverter, which is handy when we only want to invert the polarity of the input
signal.
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers
Switching in different feedback resistors, as shown in Fig.2-3, can control
the closed loop gain of the basic inverting amplifier.
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers DC output offset
In the ideal op-amp, the output voltage is zero when the input voltage is also
zero. However, all commercial op-amps have a small, but finite, dc output
voltage called the output offset voltage, even though the input may be
grounded.
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers DC output offset
The dc output offset voltage is a result of three sources:
•input offset current
• input bias current
•input offset voltage
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers DC output offset
As stated in Chapter 1, the input bias current must be supplied to both inputs
of the op-amp to assure that the op-amp behaves properly. For the inverting
amplifier circuit of Fig. 2-5, the input bias current, with no input signal, flows
through both the input and feedback resistors.
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers DC output offset
Ohm’s law, when a current flows through a known resistance develops a
voltage across this resistance (V = IR). Since the non-inverting input of the opamp is grounded, the voltages developed across these resistors appear as a
dc input voltage, which in turn is amplified by the op-amp.
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers DC output offset
For the inverting amplifier circuit of Fig. 2-5, the output voltage (V0S)
generated as a result of the input bias current (IB) is:
V OS=IBR2
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers DC output offset
The method commonly used to correct for the output voltage offset due to
the input bias current is to place an additional resistor R3 between the noninverting (±) input and ground as shown in the figure below.
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers DC output offset
The value of this additional resistor is equal to the parallel combination of R1
and R2, or:
R1 R2
R3 
R1  R2
so that the voltage developed across R3 is equal and opposite to the
voltage across the parallel combination of R1 and R2. Since the two
voltages are equal and opposite, they cancel.
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers DC output offset
However, the above discussion assumes that the bias currents flowing into
both inputs are equal. Unfortunately, in a typical op-amp, both bias currents
are not exactly equal, the value for Ib (from the data sheet) being only an
average of the two input bias currents.
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers DC output offset
Since there will be a difference in the two bias currents, called the Input
offset current, Ios, there will still exist a small but finite dc output offset voltage,
equal to:
Vos = IosR2
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers DC output offset
The remaining source of output offset is due to the op-amp’s input offset
voltage, resulting from mismatches in the internal circuitry and fabrication of
the op-amp. As shown for the inverting amplifier circuit of Fig. 2-7, the input
offset voltage ,Voi, can be represented as a small battery in series with the
non-inverting input of an ideal op-amp. (as shown above)
Chapter 2
Basic Linear Amplifier Circuits
lnverting Amplifiers DC output offset
For the circuit in Fig. 2-7, the dc output offset voltage, as a result the input
offset voltage, is calculated from:
 R2 
VOS  1   * Voi
 R1 