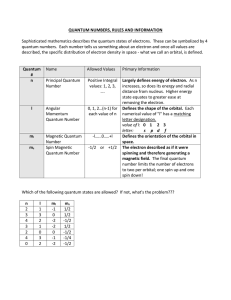
Quantum Model Worksheet
... PART A – WAVES & QUANTUM MECHANICS 1. What experimental evidence supported de Broglie’s idea that electrons have wave-like properties? ...
... PART A – WAVES & QUANTUM MECHANICS 1. What experimental evidence supported de Broglie’s idea that electrons have wave-like properties? ...
Problem set 7
... Quantum Mechanics 3, Spring 2012 CMI Problem set 7 Due by beginning of class on Monday Mar 5, 2012 BCH formula for x and p , SHO 1. Consider the function f (t) = etA Be−tA where A, B are a pair of operators (e.g. position and momentum or creation and annihilation operators etc.). t is a parameter wh ...
... Quantum Mechanics 3, Spring 2012 CMI Problem set 7 Due by beginning of class on Monday Mar 5, 2012 BCH formula for x and p , SHO 1. Consider the function f (t) = etA Be−tA where A, B are a pair of operators (e.g. position and momentum or creation and annihilation operators etc.). t is a parameter wh ...
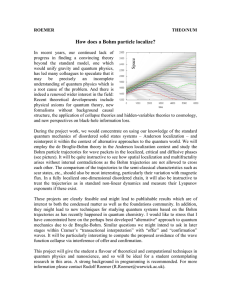
How does a Bohm particle localize?
... employ the de Broglie-Bohm theory in the Anderson localization context and study the Bohm particle trajectories for wave packets in the localized, critical and diffusive phases (see picture). It will be quite instructive to see how spatial localization and multifractality arises without internal con ...
... employ the de Broglie-Bohm theory in the Anderson localization context and study the Bohm particle trajectories for wave packets in the localized, critical and diffusive phases (see picture). It will be quite instructive to see how spatial localization and multifractality arises without internal con ...
1 Lecture 10 Summary Phys 404 Statistical
... derived in 1911 as an early application of quantum mechanics to statistical physics (note that there is an in ). Although the energy and pressure of the ideal gas do not include , the Helmholtz free energy and entropy both have it. This shows that quantum mechanics is the essential starting point fo ...
... derived in 1911 as an early application of quantum mechanics to statistical physics (note that there is an in ). Although the energy and pressure of the ideal gas do not include , the Helmholtz free energy and entropy both have it. This shows that quantum mechanics is the essential starting point fo ...
HOMEWORK ASSIGNMENT 5: Solutions
... (e) Assuming that the spin-orbit interaction lifts the degeneracy of the states with different j, how many distinct energy levels make up the fine-structure of the (3p)2 state? The allowed j values are j = 0, 1, 2, so there would be 3 fine-structure levels. (f) Which j levels would shift if a contac ...
... (e) Assuming that the spin-orbit interaction lifts the degeneracy of the states with different j, how many distinct energy levels make up the fine-structure of the (3p)2 state? The allowed j values are j = 0, 1, 2, so there would be 3 fine-structure levels. (f) Which j levels would shift if a contac ...
Planck`s Law and Light Quantum Hypothesis.
... that is, the relation between the radiation density and the mean energy of an oscillator, and they make assumptions about the number of degrees of freedom of the ether, which appear in the above formula (the first factor on the right– hand side). This factor, however, can be derived only from classi ...
... that is, the relation between the radiation density and the mean energy of an oscillator, and they make assumptions about the number of degrees of freedom of the ether, which appear in the above formula (the first factor on the right– hand side). This factor, however, can be derived only from classi ...
Information quantique
... clock. Quantum cryptography, where the use of quantum objects (typically photons) as information carriers makes it possible to detect eavesdroppers due to fundamental measurement back-action. Quantum computing, where qubits replace classical bits. For some specific algorithms, “quantum parallelism” ...
... clock. Quantum cryptography, where the use of quantum objects (typically photons) as information carriers makes it possible to detect eavesdroppers due to fundamental measurement back-action. Quantum computing, where qubits replace classical bits. For some specific algorithms, “quantum parallelism” ...
Document
... H H I H II We only “see” universe # I. Information to and from universe II is lost. We may indeed impose the constraint: H II ...
... H H I H II We only “see” universe # I. Information to and from universe II is lost. We may indeed impose the constraint: H II ...
ON THE UNCERTAINTY RELATIONS IN STOCHASTIC MECHANICS IVAÏLO M. MLADENOV
... DIMITAR A. TRIFONOV, BLAGOVEST A. NIKOLOV AND IVAÏLO M. MLADENOV Presented by Ivaïlo M. Mladenov Abstract. It is shown that the Bohm equations for the phase S and squared modulus ρ of the quantum mechanical wave function can be derived from the classical ensemble equations admiting an aditional mome ...
... DIMITAR A. TRIFONOV, BLAGOVEST A. NIKOLOV AND IVAÏLO M. MLADENOV Presented by Ivaïlo M. Mladenov Abstract. It is shown that the Bohm equations for the phase S and squared modulus ρ of the quantum mechanical wave function can be derived from the classical ensemble equations admiting an aditional mome ...
Emergence of Modern Science
... It is currently necessary to use quantum mechanics to understand the behavior of systems at atomic length scales and smaller. ...
... It is currently necessary to use quantum mechanics to understand the behavior of systems at atomic length scales and smaller. ...
INTRODUCTION TO ELEMENTARY PARTICLE PHYSICS
... task. Ordinarily, the procedure is to guess a form for the interaction and compare the resulting theoretical calculations with the ...
... task. Ordinarily, the procedure is to guess a form for the interaction and compare the resulting theoretical calculations with the ...
Quantum Mechanics
... (ii) If the integral is infinite for some wave functions, no factor to make it been normalizable. The non-normalizable wave function cannot represent particles. (iii) the condition of wave function which can be normalizable ...
... (ii) If the integral is infinite for some wave functions, no factor to make it been normalizable. The non-normalizable wave function cannot represent particles. (iii) the condition of wave function which can be normalizable ...
Physics 411: Introduction to Quantum Mechanics
... Brief course description: Introduction to Quantum Mechanics is a two-semester course (411 and 412) and is mandatory for all physics majors pursuing the Academic Physics Concentration. Roughly speaking, 411 deals with the foundations and development of quantum theory whereas 412 is more geared toward ...
... Brief course description: Introduction to Quantum Mechanics is a two-semester course (411 and 412) and is mandatory for all physics majors pursuing the Academic Physics Concentration. Roughly speaking, 411 deals with the foundations and development of quantum theory whereas 412 is more geared toward ...
Quantum Information (QI) - BYU Physics and Astronomy
... How do I pass this 513R class? What will we do? CP, HW, IP, MT, F How do you communicate? Sources for QI? (Linear Algebra prerequisite) What is Linear Algebra? ...
... How do I pass this 513R class? What will we do? CP, HW, IP, MT, F How do you communicate? Sources for QI? (Linear Algebra prerequisite) What is Linear Algebra? ...
What is Entanglement? Entangled Fields Looking at Entangled
... cannot really be considered as separate objects, but are intrinsically connected or “entangled” with each other. For example, performing a measurement on one, such as measuring the particles spin as in the diagram above, instantaneously affects the result of measuring the other. This phenomena occur ...
... cannot really be considered as separate objects, but are intrinsically connected or “entangled” with each other. For example, performing a measurement on one, such as measuring the particles spin as in the diagram above, instantaneously affects the result of measuring the other. This phenomena occur ...
Anmeldeformular für Email
... Since classical physics is described in phase space and quantum mechanics in Hilbert space a unified picture is desired. This is provided, for instance, by the so called Wigner function (WF), which has remarkable properties: It transform s the wave function of a quantum mechanical particle (or the d ...
... Since classical physics is described in phase space and quantum mechanics in Hilbert space a unified picture is desired. This is provided, for instance, by the so called Wigner function (WF), which has remarkable properties: It transform s the wave function of a quantum mechanical particle (or the d ...