2.3 Lesson
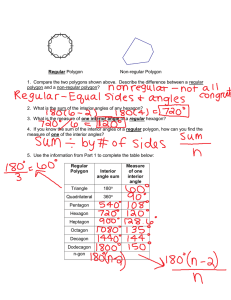
... d) Use the function S(n) = 180(n-2) to determine the sum of the interior angles of a regular octagon. Compare your answer with the sum you determined in part c) ...
... d) Use the function S(n) = 180(n-2) to determine the sum of the interior angles of a regular octagon. Compare your answer with the sum you determined in part c) ...
12.1 Exploring Solids
... • Polyhedron: a three-dimensional solid made up of plane faces. Poly=many Hedron=faces • Prism: a polyhedron (geometric solid) with two parallel, same-size bases joined by 3 or more parallelogram-shaped sides. • Tetrahedron: polyhedron with four faces (tetra=four, hedron=face). ...
... • Polyhedron: a three-dimensional solid made up of plane faces. Poly=many Hedron=faces • Prism: a polyhedron (geometric solid) with two parallel, same-size bases joined by 3 or more parallelogram-shaped sides. • Tetrahedron: polyhedron with four faces (tetra=four, hedron=face). ...
worksheet - hrsbstaff.ednet.ns.ca
... Intro: a polygon is defined as a shape on a plane (a 2D shape) that is bounded by a certain number of straight line segments that form a loop. Examples at right: We often think of polygons like rectangles, triangles, pentagons, where the internal angles at each vertex are less than 180o… These are e ...
... Intro: a polygon is defined as a shape on a plane (a 2D shape) that is bounded by a certain number of straight line segments that form a loop. Examples at right: We often think of polygons like rectangles, triangles, pentagons, where the internal angles at each vertex are less than 180o… These are e ...
Polygons - My CCSD
... (1) The student will be able to identify, name, and describe polygons. (2) The student will be able to find the sum of the measures of the interior angles of a quadrilateral. Toolbox: Summary: Polygon – is a plane figure that is formed By 3 or more segments (sides) such that No 2 sides with a common ...
... (1) The student will be able to identify, name, and describe polygons. (2) The student will be able to find the sum of the measures of the interior angles of a quadrilateral. Toolbox: Summary: Polygon – is a plane figure that is formed By 3 or more segments (sides) such that No 2 sides with a common ...
40 Regular Polygons
... Angles of interest in a regular n-gon are the following: A vertex angle (also called an interior angle) is formed by two consecutive sides. A central angle is formed by the segments connecting two consecutive vertices to the center of the regular n-gon. An exterior angle is formed by one side toget ...
... Angles of interest in a regular n-gon are the following: A vertex angle (also called an interior angle) is formed by two consecutive sides. A central angle is formed by the segments connecting two consecutive vertices to the center of the regular n-gon. An exterior angle is formed by one side toget ...
TestGen HTML Exam
... 15. If each angle of a regular polygon measures 108°, how many sides does it have? A) 5 sides B) 3 sides C) 4 sides D) 7 sides Same approach as in 11. Suppose the polygon has n sides. Such a polygon can be split into n-2 triangles by drawing all the diagonals from one vertex. It follows that the sum ...
... 15. If each angle of a regular polygon measures 108°, how many sides does it have? A) 5 sides B) 3 sides C) 4 sides D) 7 sides Same approach as in 11. Suppose the polygon has n sides. Such a polygon can be split into n-2 triangles by drawing all the diagonals from one vertex. It follows that the sum ...
Polygons and Quadrilaterals
... volume, and angle measure, are measureable. Units are used to describe these attributes. Definitions establish meanings and remove possible misunderstanding. Other truths are more complex and difficult to see. It is often possible to verify complex truths by reasoning from simpler ones using deducti ...
... volume, and angle measure, are measureable. Units are used to describe these attributes. Definitions establish meanings and remove possible misunderstanding. Other truths are more complex and difficult to see. It is often possible to verify complex truths by reasoning from simpler ones using deducti ...
Hyperbolic Geometry
... All right angles are congruent If a straight line intersects two other straight lines, and so makes the two interior angles on one side of it together less than two right angles, then the other straight lines will meet at a point if extended far enough on the side on which the angles are less than t ...
... All right angles are congruent If a straight line intersects two other straight lines, and so makes the two interior angles on one side of it together less than two right angles, then the other straight lines will meet at a point if extended far enough on the side on which the angles are less than t ...
Tessellation Simulation Project
... below. Mark a few places where these things occur in your tessellation. Once you have completed it, print it out and hand it in. ...
... below. Mark a few places where these things occur in your tessellation. Once you have completed it, print it out and hand it in. ...
List of regular polytopes and compounds
This page lists the regular polytopes and regular polytope compounds in Euclidean, spherical and hyperbolic spaces.The Schläfli symbol describes every regular tessellation of an n-sphere, Euclidean and hyperbolic spaces. A Schläfli symbol describing an n-polytope equivalently describes a tessellation of a (n-1)-sphere. In addition, the symmetry of a regular polytope or tessellation is expressed as a Coxeter group, which Coxeter expressed identically to the Schläfli symbol, except delimiting by square brackets, a notation that is called Coxeter notation. Another related symbol is the Coxeter-Dynkin diagram which represents a symmetry group with no rings, and the represents regular polytope or tessellation with a ring on the first node. For example the cube has Schläfli symbol {4,3}, and with its octahedral symmetry, [4,3] or File:CDel node.pngFile:CDel 4.pngFile:CDel node.pngFile:CDel 3.pngFile:CDel node.png, is represented by Coxeter diagram File:CDel node 1.pngFile:CDel 4.pngFile:CDel node.pngFile:CDel 3.pngFile:CDel node.png.The regular polytopes are grouped by dimension and subgrouped by convex, nonconvex and infinite forms. Nonconvex forms use the same vertices as the convex forms, but have intersecting facets. Infinite forms tessellate a one-lower-dimensional Euclidean space.Infinite forms can be extended to tessellate a hyperbolic space. Hyperbolic space is like normal space at a small scale, but parallel lines diverge at a distance. This allows vertex figures to have negative angle defects, like making a vertex with seven equilateral triangles and allowing it to lie flat. It cannot be done in a regular plane, but can be at the right scale of a hyperbolic plane.A more general definition of regular polytopes which do not have simple Schläfli symbols includes regular skew polytopes and regular skew apeirotopes with nonplanar facets or vertex figures.























