Section 2.2 part 2
... figure are the same length. • Equiangular – all of the angles in the figure have the same measure. • Regular – all of the sides are the same length and all of the angles have the same measure. ...
... figure are the same length. • Equiangular – all of the angles in the figure have the same measure. • Regular – all of the sides are the same length and all of the angles have the same measure. ...
topic 8-2: similar polygons
... a) Name the angle included between AM and MC:__________ b) Name the side included between A and M:__________ c) Name the side included between A and C:__________ ...
... a) Name the angle included between AM and MC:__________ b) Name the side included between A and M:__________ c) Name the side included between A and C:__________ ...
Fabian assignment
... Corollary 3.4 (Descartes). In a convex polyhedron, the sum of the defects at all the vertices is equal to 4π. ...
... Corollary 3.4 (Descartes). In a convex polyhedron, the sum of the defects at all the vertices is equal to 4π. ...
EXPLORYNG POLYGONS AND AREA
... began experimenting with dividing the sides of triangles by other numbers. Ryan eventually found that dividing a triangle’s sides by any odd number and connecting the endpoints of each middle segment to the opposite vertex also forms a hexagon. 6 ...
... began experimenting with dividing the sides of triangles by other numbers. Ryan eventually found that dividing a triangle’s sides by any odd number and connecting the endpoints of each middle segment to the opposite vertex also forms a hexagon. 6 ...
Part 1: Interior Angles in Polygons
... 2. For each of the tessellations above, look at the vertices where several polygons meet. What is the sum of the angles around each vertex? 3. For each of the following regular polygons, demonstrate how each would tessellate a plane, or show why the polygons do not tessellate. ...
... 2. For each of the tessellations above, look at the vertices where several polygons meet. What is the sum of the angles around each vertex? 3. For each of the following regular polygons, demonstrate how each would tessellate a plane, or show why the polygons do not tessellate. ...
1 - shurenribetgeometryclass
... respect to a point (dilation of a geometric figure) or with respect to the axis of a graph (dilation of a graph). Note: Some high school textbooks erroneously use the word dilation to refer to all transformations in which the figure changes size, whether the figure becomes larger or smaller. Unfortu ...
... respect to a point (dilation of a geometric figure) or with respect to the axis of a graph (dilation of a graph). Note: Some high school textbooks erroneously use the word dilation to refer to all transformations in which the figure changes size, whether the figure becomes larger or smaller. Unfortu ...
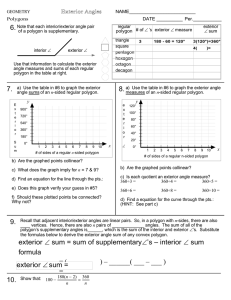
For each REGULAR polygon, find the SUM of the interior angles
... For each REGULAR polygon, find the SUM of the interior angles AND EACH interior angle. 1. Regular Nonagon ...
... For each REGULAR polygon, find the SUM of the interior angles AND EACH interior angle. 1. Regular Nonagon ...
Two Dimensional Areas Crossword
... circle, then the diameter will be the triangle's _____. Two chords that are equidistant from the center of a circle, such as the sides of a regular polygon inscribed in the circle, are always ____. (two words) To compute the area of a rhombus, one must calculate half the product of its _____. The ar ...
... circle, then the diameter will be the triangle's _____. Two chords that are equidistant from the center of a circle, such as the sides of a regular polygon inscribed in the circle, are always ____. (two words) To compute the area of a rhombus, one must calculate half the product of its _____. The ar ...
Answer Key -- Adding It All Up - Illuminations
... 3. Determine the formula that you would use to find the angle sum of an n-gon. Sum = 180(n – 2) 4. What is special about a regular polygon? How would you find the measure of each interior angle of a regular polygon if you knew the number of sides? (Hint: Use the table on page 1 to find a pattern. T ...
... 3. Determine the formula that you would use to find the angle sum of an n-gon. Sum = 180(n – 2) 4. What is special about a regular polygon? How would you find the measure of each interior angle of a regular polygon if you knew the number of sides? (Hint: Use the table on page 1 to find a pattern. T ...
List of regular polytopes and compounds
This page lists the regular polytopes and regular polytope compounds in Euclidean, spherical and hyperbolic spaces.The Schläfli symbol describes every regular tessellation of an n-sphere, Euclidean and hyperbolic spaces. A Schläfli symbol describing an n-polytope equivalently describes a tessellation of a (n-1)-sphere. In addition, the symmetry of a regular polytope or tessellation is expressed as a Coxeter group, which Coxeter expressed identically to the Schläfli symbol, except delimiting by square brackets, a notation that is called Coxeter notation. Another related symbol is the Coxeter-Dynkin diagram which represents a symmetry group with no rings, and the represents regular polytope or tessellation with a ring on the first node. For example the cube has Schläfli symbol {4,3}, and with its octahedral symmetry, [4,3] or File:CDel node.pngFile:CDel 4.pngFile:CDel node.pngFile:CDel 3.pngFile:CDel node.png, is represented by Coxeter diagram File:CDel node 1.pngFile:CDel 4.pngFile:CDel node.pngFile:CDel 3.pngFile:CDel node.png.The regular polytopes are grouped by dimension and subgrouped by convex, nonconvex and infinite forms. Nonconvex forms use the same vertices as the convex forms, but have intersecting facets. Infinite forms tessellate a one-lower-dimensional Euclidean space.Infinite forms can be extended to tessellate a hyperbolic space. Hyperbolic space is like normal space at a small scale, but parallel lines diverge at a distance. This allows vertex figures to have negative angle defects, like making a vertex with seven equilateral triangles and allowing it to lie flat. It cannot be done in a regular plane, but can be at the right scale of a hyperbolic plane.A more general definition of regular polytopes which do not have simple Schläfli symbols includes regular skew polytopes and regular skew apeirotopes with nonplanar facets or vertex figures.