Reference - Department of Statistics, Yale
... Amongst the sources for my notes were the following books, all of which I recommend. Ash, R. B. Real Analysis and Probability Good background on measure theory, particularly the connections between topology and measure. Recommended for martingales and conditioning. Billingsley, P. Probability and Me ...
... Amongst the sources for my notes were the following books, all of which I recommend. Ash, R. B. Real Analysis and Probability Good background on measure theory, particularly the connections between topology and measure. Recommended for martingales and conditioning. Billingsley, P. Probability and Me ...
Math 115
... 1) If an event must occur, we assign it a probability of: a) –1 b) 1 c) 0.50 d) 0 2) The expected value of a probability distribution is the same as the a) mean. b) standard deviation. c) variance. d) median. 3) If a random variable may take on any value then the random variable is said to be a) ran ...
... 1) If an event must occur, we assign it a probability of: a) –1 b) 1 c) 0.50 d) 0 2) The expected value of a probability distribution is the same as the a) mean. b) standard deviation. c) variance. d) median. 3) If a random variable may take on any value then the random variable is said to be a) ran ...
PROBABILITY THEORY
... • The search for a widely acceptable definition took nearly three centuries and was marked by much controversy. • The matter was finally resolved in the 20th century by treating probability theory on an axiomatic basis. • In 1933 a monograph Grundbegriffe der Wahrscheinlichkeitsrechnun (Foundations ...
... • The search for a widely acceptable definition took nearly three centuries and was marked by much controversy. • The matter was finally resolved in the 20th century by treating probability theory on an axiomatic basis. • In 1933 a monograph Grundbegriffe der Wahrscheinlichkeitsrechnun (Foundations ...
1 CHANCE AND MACROEVOLUTION
... provides a useful starting point for a discussion of the meaning of chance in evolutionary theory, but it is in need of further clarification. In particular, there are three conceptions of chance implicit in Eble’s “statistical meaning,” not two. In the first of the two statistical meanings of chanc ...
... provides a useful starting point for a discussion of the meaning of chance in evolutionary theory, but it is in need of further clarification. In particular, there are three conceptions of chance implicit in Eble’s “statistical meaning,” not two. In the first of the two statistical meanings of chanc ...
Chapter 5 Foundations of Bayesian Networks
... distributions of all nodes given their parents in G, whenever these conditional distributions exist. It is important to realize that we can’t take just any DAG and expect a joint distribution to equal the product of its conditional distributions in the DAG. This is only true if the Markov condition ...
... distributions of all nodes given their parents in G, whenever these conditional distributions exist. It is important to realize that we can’t take just any DAG and expect a joint distribution to equal the product of its conditional distributions in the DAG. This is only true if the Markov condition ...
Sec. 6.3 Part 2 Blank Notes
... The probability of ____________________________ is then found by __________________________of all branches that are part of ________________ ...
... The probability of ____________________________ is then found by __________________________of all branches that are part of ________________ ...
File
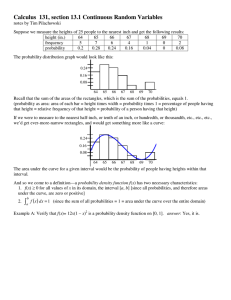
... 3 5 2 1 5 2 3 5 4 9 boxes 4 3 5 3 5 1 1 1 5 3 1 5 4 5 2 15 boxes 5 5 5 2 4 1 2 1 5 3 10 boxes We never had to buy more than 22 boxes to get the full set of cards in 50 repetitions of our simulation. Our estimate of the probability that it takes 23 or more boxes to get a full set is roughly 0. ...
... 3 5 2 1 5 2 3 5 4 9 boxes 4 3 5 3 5 1 1 1 5 3 1 5 4 5 2 15 boxes 5 5 5 2 4 1 2 1 5 3 10 boxes We never had to buy more than 22 boxes to get the full set of cards in 50 repetitions of our simulation. Our estimate of the probability that it takes 23 or more boxes to get a full set is roughly 0. ...
1.017 Class 10: Common Distributions
... A random variable is a function (or rule) x() that associates a real number x with each outcome in the sample space S of an experiment. Assignment of such rules enables us to quantify a wide range of real-world experimental outcomes. Example: Experiment: Toss of a coin Outcome: Heads or tails Ran ...
... A random variable is a function (or rule) x() that associates a real number x with each outcome in the sample space S of an experiment. Assignment of such rules enables us to quantify a wide range of real-world experimental outcomes. Example: Experiment: Toss of a coin Outcome: Heads or tails Ran ...
Conditional probability and independence Bernoulli trials and the
... Bernoulli Trials The prototype of the Bernoulli trials process is repeated coin tossing. This is generalized in the Bernoulli trials model. 1. In each trial there are two distinct possible outcomes: “success” or “failure.” 2. The probability of success p is the same in every trial. (For convenience, ...
... Bernoulli Trials The prototype of the Bernoulli trials process is repeated coin tossing. This is generalized in the Bernoulli trials model. 1. In each trial there are two distinct possible outcomes: “success” or “failure.” 2. The probability of success p is the same in every trial. (For convenience, ...