8.2 Integration by Parts
... 2. Perform long division on the fraction of polynomials 3. Find a partial fraction decomposition of the remaining fraction (if there is one) If you follow these steps correctly, you should be able to integrate any rational function whatsoever. But if you follow them incorrectly... well, that’s not a ...
... 2. Perform long division on the fraction of polynomials 3. Find a partial fraction decomposition of the remaining fraction (if there is one) If you follow these steps correctly, you should be able to integrate any rational function whatsoever. But if you follow them incorrectly... well, that’s not a ...
Lecture10
... a) Recall that a random variable X is simply a function from a sample space S into the real numbers. The random variable is discrete is the range of X is finite or countably infinite. This refers to the number of values X can take on, not the size of the values. The random variable is continuous if ...
... a) Recall that a random variable X is simply a function from a sample space S into the real numbers. The random variable is discrete is the range of X is finite or countably infinite. This refers to the number of values X can take on, not the size of the values. The random variable is continuous if ...
Basic concept of differential and integral calculus
... Following are some of the standard derivative:- ...
... Following are some of the standard derivative:- ...
Unit 3. Integration 3A. Differentials, indefinite integration
... b) Graph the solution and use the graph to discuss the range of validity of the formula for y. In particular, explain why the apparent value at x = 3/2 is suspect. 3F-4 Newton’s law of cooling says that the rate of change of temperature is proportional to the temperature difference. In symbols, if a ...
... b) Graph the solution and use the graph to discuss the range of validity of the formula for y. In particular, explain why the apparent value at x = 3/2 is suspect. 3F-4 Newton’s law of cooling says that the rate of change of temperature is proportional to the temperature difference. In symbols, if a ...
Chapter 1
... Continuity on an Open Interval: A function is continuous on an open interval (a, b) if it is continuous at each point in the interval. A function that is continuous on the entire real line (-¥,¥) is everywhere continuous. If a function is not continuous on an open interval is it said to have a disco ...
... Continuity on an Open Interval: A function is continuous on an open interval (a, b) if it is continuous at each point in the interval. A function that is continuous on the entire real line (-¥,¥) is everywhere continuous. If a function is not continuous on an open interval is it said to have a disco ...
Math 131The Fundamental Theorem of Calculus (Part 2)
... • The limit was a definite integral • which we could evaluate easily (if we know an antiderivative) using the First Fundamental Theorem of Calculus. We will use this process repeatedly over the next few weeks. Look for it in other courses. What quantities do you know are ‘products’? What about the a ...
... • The limit was a definite integral • which we could evaluate easily (if we know an antiderivative) using the First Fundamental Theorem of Calculus. We will use this process repeatedly over the next few weeks. Look for it in other courses. What quantities do you know are ‘products’? What about the a ...
Area under a Graph
... of f (x). If F (x) = f (x) dx is an arbitrary anti-derivative of f (x), we must have, for some constant C: A(x) = F (x) + C We also know an intial value for A(x). The region Ra has its right wall is equal to its left wall, meaning it has no width. We thus have A(a) = Area(Ra ) = 0. Thus A(a) = F (a) ...
... of f (x). If F (x) = f (x) dx is an arbitrary anti-derivative of f (x), we must have, for some constant C: A(x) = F (x) + C We also know an intial value for A(x). The region Ra has its right wall is equal to its left wall, meaning it has no width. We thus have A(a) = Area(Ra ) = 0. Thus A(a) = F (a) ...
Test #2 Review
... How to tell if the limit of f(x,y) as x, y tends to a, b exists and how to find its value. How to find partial derivatives, and second order partial & mixed partial derivatives; and how to use the chain rules. How to find total differentials and how to use them to estimate percentage errors in m ...
... How to tell if the limit of f(x,y) as x, y tends to a, b exists and how to find its value. How to find partial derivatives, and second order partial & mixed partial derivatives; and how to use the chain rules. How to find total differentials and how to use them to estimate percentage errors in m ...
Improper Integrals
... be found, a f (x) dx always existed, and was a number. In this section, we investigate what happens when these conditions are not met. Definition 1 (Improper Integral) An integral is an improper integral if either the interval of integration is not finite (improper integral of type 1) or if the funct ...
... be found, a f (x) dx always existed, and was a number. In this section, we investigate what happens when these conditions are not met. Definition 1 (Improper Integral) An integral is an improper integral if either the interval of integration is not finite (improper integral of type 1) or if the funct ...
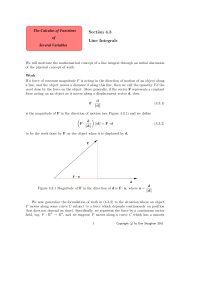
Section 4.3 Line Integrals - The Calculus of Functions of Several
... in agreement with an earlier example. Similarly, if E is the unit circle in R2 centered at the origin, then we know that Z y 2 dx + 2xydy = 0, E ...
... in agreement with an earlier example. Similarly, if E is the unit circle in R2 centered at the origin, then we know that Z y 2 dx + 2xydy = 0, E ...
Double Integrals over Rectangular Regions
... 33. Suppose the random variables X and Y measure the length of time (in days) that a patient stays in the hospital after abdominal and orthopedic surgery, respectively. On Monday, the patient in bed 107A undergoes an emergency appendectomy while her roommate in bed 107B undergoes (orthopedic) surger ...
... 33. Suppose the random variables X and Y measure the length of time (in days) that a patient stays in the hospital after abdominal and orthopedic surgery, respectively. On Monday, the patient in bed 107A undergoes an emergency appendectomy while her roommate in bed 107B undergoes (orthopedic) surger ...
An Introduction to Double Integrals Math Insight Suppose that you
... where the sum is over all rectangles. If in the above picture, each rectangle were 75 millimeters wide and 65 millimeters high, then the resulting estimate of the total number of hairs would be (9+9+8+17+9+3+1+1+11+8+10+8+1+2+3+8+7+2+5+3)⋅75⋅65=609,375 6. The above result is only a rough estimate be ...
... where the sum is over all rectangles. If in the above picture, each rectangle were 75 millimeters wide and 65 millimeters high, then the resulting estimate of the total number of hairs would be (9+9+8+17+9+3+1+1+11+8+10+8+1+2+3+8+7+2+5+3)⋅75⋅65=609,375 6. The above result is only a rough estimate be ...