Homogenization Rate of Diffusive Tracers in Chaotic Advection
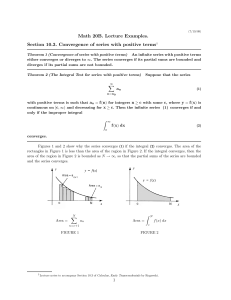
... Calculus is a subject about the study of limiting processes and it consist of three basic concepts: limit, differentiation, and integration. ...
... Calculus is a subject about the study of limiting processes and it consist of three basic concepts: limit, differentiation, and integration. ...
educative commentary on jee 2014 advanced mathematics papers
... that now that the number of candidates appearing for the JEE (Advanced) is manageable enough to permit evaluation by humans, the classic practice of requiring the candidates to give justifications for their answers would be revived at least from 2014, if not from 2013 (when there might not have been ...
... that now that the number of candidates appearing for the JEE (Advanced) is manageable enough to permit evaluation by humans, the classic practice of requiring the candidates to give justifications for their answers would be revived at least from 2014, if not from 2013 (when there might not have been ...
(a) f(x) - Portal UniMAP
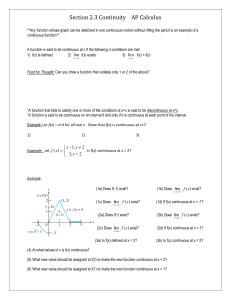
... • The first derivative test can also be used to determine the critical points. • However, it is used only if the second derivative test fails. • Three steps are required in the first derivative test. 1. Find f' (x). 2. Let f' (x) = 0 and solve for critical values, c. 3. Select points in the neighbou ...
... • The first derivative test can also be used to determine the critical points. • However, it is used only if the second derivative test fails. • Three steps are required in the first derivative test. 1. Find f' (x). 2. Let f' (x) = 0 and solve for critical values, c. 3. Select points in the neighbou ...
HOW TO USE INTEGRALS - University of Hawaii Mathematics
... (The last two formulas could also be represented by rectangles, but in this case the horizontal side of the rectangle would be a one-dimensional representative area or volume. In these cases, it’s more useful to represent the equation by a three or four-dimensional figure rather than by a rectangle. ...
... (The last two formulas could also be represented by rectangles, but in this case the horizontal side of the rectangle would be a one-dimensional representative area or volume. In these cases, it’s more useful to represent the equation by a three or four-dimensional figure rather than by a rectangle. ...
boundary behavior of poisson integrals on symmetric spaces
... In the case of [16] and [17] this does not involve an actual extension, we shall only show that the type of convergence used there is equivalent with our general notion of restricted admissible convergence. In §1 we transform the Poisson integral from an integral on the boundary to an integral on a ...
... In the case of [16] and [17] this does not involve an actual extension, we shall only show that the type of convergence used there is equivalent with our general notion of restricted admissible convergence. In §1 we transform the Poisson integral from an integral on the boundary to an integral on a ...
Developing the Calculus
... Given these statements, we see that dx ∫a Observe that, using purely geometric methods, Barrow was able to arrive at this conclusion. He did not actually use the functional notation, nor did he realize the importance of the calculations that he was making. Therefore, it is not proper to say that Bar ...
... Given these statements, we see that dx ∫a Observe that, using purely geometric methods, Barrow was able to arrive at this conclusion. He did not actually use the functional notation, nor did he realize the importance of the calculations that he was making. Therefore, it is not proper to say that Bar ...
Quasi-complete vector spaces
... for any F in the continuous linear dual of V . But although the vector I is certainly unique, why does it exist? Why is there a vector I in v actually satisfying this equation? In other words, we have defined the intetgral in the double dual of V , but why is it actually in V ? That’s the first ques ...
... for any F in the continuous linear dual of V . But although the vector I is certainly unique, why does it exist? Why is there a vector I in v actually satisfying this equation? In other words, we have defined the intetgral in the double dual of V , but why is it actually in V ? That’s the first ques ...