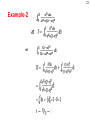Download Basic concept of differential and integral calculus

Basic Concept of
Differential and Integral Calculus
CPT Section D Quantitative Aptitude Chapter 9
Dr. Atul Kumar Srivastava
2
Learning Objectives
Understand the use of this Branch of mathematics in various branches of science
and Humanities
Understand the basics of differentiation and integration
Know how to compute derivative of a function by the first principal, derivative
of a function by the use of various formulae and higher order differentiation
Make familiar with various techniques of integration
Understand the concept of definite integrals of functions and its properties.
Differential calculus-Outlines
3
What is Differential Calculus – An Introduction
Derivative or Deferential Coefficient (First Principal Definition)
Basic Formulas
Laws for Differentiation (Algebra of Derivative of Functions)
Derivative of A Function of Function (Chain Rule)
.Derivative of Implicit Function
.Derivative of Function In Parametric Form
What is differential calculus – an 4
introduction
One of the most fundamental operations in calculus is that of differentiation. In
the study of mathematics, there are many problems containing two quantities
such that the value of one quantity depends upon the other. A variation in the
value of any ones produces a variation in the value of the other. For example
the area of a square depends upon it's side. The area of circle and volume of
sphere depend upon their radius etc.
Differential calculus is the Branch of Mathematics which studies changes
To express the rate of change of any function we introduce concept of
derivative. The concept involves a very small change in the dependent variable
with reference to a very small change in the independent variable
5
Continued
y=f(x)
•
•
x - Independent variable
y - Dependent Variable
Thus differentiation is a process of finding the derivative of a
continuous function. It is defined as the limiting value of the
ratio of the change in the function corresponding to small
change in the independent variable as the later tends to zero.
Derivative or differential coefficient
(First principal definition)
Derivative of
6
is defined as
(1)
is a function
where
is small increment in x
corresponding increment in y or f(x)
(1) Is denoted as
known as differential coefficient of
definition.
The derivative of f(x) is also
w.r.t. x
The above process of differentiation is called the first principal
7
Examples of differentiation from
first principal:
Example :1
We have
8
Example-2
f(x)=a where a is fixed real number
9
Example-3
Basic Formulas
10
Following are some of the standard derivative:-
Laws for differentiation
11
(Algebra of derivative of functions)
Let f(x) and g(x) be two functions such that
their derivatives are defined in a common
domain. Then
1.Sum Rule
2.Difference Rule
3.Product Rule
12
Continued
4.(Quotient Rule)
5.
6.
13
EXAMPLES
Example-1
Find
14
Example-2
15
Example-3
16
Derivative of implicit function
Until now we have been differentiating various
function given in the form y=f(x)
But it is not necessary that functions are always
expressed in this form. For example consider one
of the following relationship between x and y
NEXT SLIDE….
17
Continued….
In the first case we can solve y and rewrite the
relationship as
In second case it does not seem easy to solve for Y.
When it is easy to express the relation as y=f(x) we
say that y is given as an explicit function of x,
otherwise it is an implicit function of x
Now we will attempt to find
for implicit function
Examples
Example 1
Find
18
for
NEXT SLIDE….
Continued
19
Example-2
20
…..(1)
Differentiating on both sides
NEXT SLIDE….
Continued
21
Derivative of functions in
parametric forms
If relation between two variables is expressed via
third variable. The third variable is called parameter.
More precisely a relation expressed between two
variables x and y in the form x=f(t),y=g(t) is said to
be parametric form with t is a parameter.
In order to find derivative of function in such form, we
have by chain rule.
22
23
Continued
24
Example 1 Find
Given That
So
Example-2
25
Logarithmic differentiation
.
26
and
We differentiate such functions by taking logarithm on both
sides. This process in called logarithmic differentiate.
Examples
Example
1
Differentiate
Taking logarithms on both sides
Differentiate both sides w.r.t x
27
Example-2
28
Differentiate
29
Higher Order differentiation
If
is differentiable, we may differentiate it
w.r.t. x.
The LHS becomes
which is
called the second order derivative of
or
and is denoted by
. It is also denoted by
.
If
we remark that higher order
derivatives may be defined similarly.
30
-
EXAMPLES
Example-1
Given that
=
-
Here
=
-
31
Example-2
Differentiate again
Find
Gradient or slope of the curve
Let y=f(x)be a curve. The derivative of f(x)
at a point x represents the slope of the
tangent to the curve y=f(x)at the point x.
Sometime the derivative is called gradient
of the curve.
32
33
Example-1
Find the gradient of the curve
Given
The gradient of the curve at point X=0 is -12
Example-2
to the curve
Find the slope of the tangent
34
35
Miscellaneous Examples
Example:1
Differentiate
36
Example-2
Differentiate
Let
37
Example-3
Find derivative of
38
Example-4: Find dy /dx
differentiate implicitly w.r.t. x ., we get
39
Example-5 If
40
Example-6
Differentiate
Example 7
41
42
Example 8
43
Continued
By cross multiplication
Integral Calculus
What Is Integration (Definition)
• Basic Formulas
Method Of Substitution (Change Of Variable)
Integration By Parts
Method Of Partial Fraction
Definite Integration
Important Properties
Miscellaneous Examples
44
45
What is Integration (definition)
Integration is inverse process of differentiation. Integral calculus
deals with integration and its application. It was invented in
attempt to solve the problems of finding areas under curves and
volumes of solids of revolution.
Also we can define integration as the inverse process of
differentiation .
Constant of integration
46
and c is an arbitrary constant we also have
Evidently the integral of
is obtained by giving different
values to C . Here 'C' is called constant of integration
The process of finding the integral is called integration.
The function which is integrated is called the integrand.
Basic Formulas
47
Two Simple Theorem
1.
48
.
2.
Since integration and differentiation are inverse
process we have
Example-1
49
Example-2
Example-3
50
Evaluate
Example-4
or
Example-5
Examples
Example-6 Evaluate
Example-7 Evaluate
51
52
Example-8
By simple division
Integration By Substitution
The given integral
can be transformed into another form by changing
the independent variable x to t by substituting
Consider
Usually we make a substitution for a function whose derivation also
occur in the integrand.
53
Examples
Example1
adx = dt
54
55
Example 2
.
or
Evaluate
56
Example-3: Evaluate
or
dt
Important standard formulas
1.
2.
3.
4.
57
58
Continued
5.
6.
7.
8.
.
59
Example
Integration by Parts
It is useful method to find integration
of product of function.
Integration of product of two function
60
61
Examples
Example:1
62
Example-2
Evaluate
63
Example-3
64
Example 4
(Solve first integral only)
65
Methods of Partial Fractions
66
Type-1
Example-1
Find the partial fraction of
we put x=2
we put x=3
and get
67
Type-2
Comparing coefficients of
and constant term on both sides
Solving we get
Therefore
68
Example
Definite Integration
69
Consider indefinite integral
Now consider
Here a =
b =
lower limit of integration
upper limit of integration
is called definite integral of f(x) from a to b
Properties
70
71
Example-1:
72
Example-2
or
Miscellaneous examples
find
let
73
74
Example-2
Let
75
Example-3
integration by parts
consider
76
Example 4.
solve
where
77
Example:5
by simple division
78
Example-6
First simplify integrand
Example 7.
79
80
Example 8.
81
Example 9.
82
Example 10.
I
II
dx
Example11. Find the equation of the curve where
slope at (x,y) is 9x which passes through origin
Given
since it passes through the origin (o,o)
Then
or
83
84
Example 12.
Let
Example 13.
85
86
SUMMARY OF THE CHAPTER
Differential calculus
Continued…….
87
88
Integral Calculus
89
Continued……
=
=
=
90
Continued
=
91
Continued
,
(a < b < c)
92
Continued
=0
93
MCQ’s
Question Time
Question:1
HINT-Logarithmic Differentiation
94
95
Question.2
96
Question.3
HINT- Logarithmic differentiation then Apply product rule
97
Question.4
98
Question.5
HINT- (Apply Quotient rule)
99
Question-6
HINT - (Apply chain rule)
100
Question.7
HINT - (Apply product rule and chain rule)
Question 8
HINT- (Quotient rule)
101
102
Question.9
HINT- (Take log both sides then apply quotient rule)
103
Question.10
HINT- (Differentiation of implicit function)
104
Question.11
HINT- (Logarithmic differentiation)
105
Question:12
HINT-
(Implicit function)
106
Question.13
(d)
HINT-
(Logarithmic differentiation)
107
Question.14
HINT-
(Quotient rule)
Question.15
The value of p and q are.
HINT-
108
109
Question.16
HINT-
110
Question.17
HINT- Integrate By Parts
111
Question.18
112
Question.19
HINT- Integration by substitution let
113
Question.20
HINT- [Integration by substitution, let t
114
Question.21
HINT- [Integration by substitution let
115
Question.22
HINT-
116
Question.23
HINT-
117
Question.24
HINT- (Integration by substitution let 7x + 5 = t)
118
Question.25
HINT- Divide Numerator by Denominator then Integrate
119
Question.26
HINT-
120
Question.27
HINT-
121
Question.28
HINT-
122
Question.29
HINT-
123
Question.30
HINT-
124
Practice makes a man perfect and that’s what mathematics
demands.
.
So, students ‘all the best’ for your upcoming examinations
. keep practicing.
Thank you