Section 6.6
... study some basic principles of “work”, which is one of the fundamental concepts in physics and engineering. A simple example: When you push a car that has run out of gas for a certain distance you are performing work and the effect of your work is to make the car move. ...
... study some basic principles of “work”, which is one of the fundamental concepts in physics and engineering. A simple example: When you push a car that has run out of gas for a certain distance you are performing work and the effect of your work is to make the car move. ...
Lecture 17 - University of Chicago Math
... If you were paying close attention last lecture, you may have been wondering to yourself if there was a slicker way to evaluate definite integrals. Specifically, is there a formulaic way to find C? If you were paying any amount of attention, you will have noticed that the previous theorem we talked ...
... If you were paying close attention last lecture, you may have been wondering to yourself if there was a slicker way to evaluate definite integrals. Specifically, is there a formulaic way to find C? If you were paying any amount of attention, you will have noticed that the previous theorem we talked ...
lesson 29 the first fundamental theorem of calculus
... Up until now we have evaluated the definite integral by approximating the area under the curve using left, right, or midpoint Riemann Sums or the Trapezoidal Rule. The smaller the change in x, or in other words, the more rectangles or trapezoids used to approximate the area for more and more interva ...
... Up until now we have evaluated the definite integral by approximating the area under the curve using left, right, or midpoint Riemann Sums or the Trapezoidal Rule. The smaller the change in x, or in other words, the more rectangles or trapezoids used to approximate the area for more and more interva ...
Section 6.2
... Some situations arise where you are asked to find a function F whose derivative is a known function f. For example, an engineer who can measure the variable rate at which water is leaking from a tank might want to know the total amount leaked over a certain period of time. Also, a biologist who know ...
... Some situations arise where you are asked to find a function F whose derivative is a known function f. For example, an engineer who can measure the variable rate at which water is leaking from a tank might want to know the total amount leaked over a certain period of time. Also, a biologist who know ...
Math 108, Final Exam Checklist
... • Extreme value theorem • Fermat’s Theorem • Critical number • Closed Interval Method • Rolle’s Theorem and the Mean Value Theorem (MVT) • Constancy of functions with f 0 = 0. • Definition of increasing and decreasing on an interval. • Increasing/decreasing test • First derivative test for local ext ...
... • Extreme value theorem • Fermat’s Theorem • Critical number • Closed Interval Method • Rolle’s Theorem and the Mean Value Theorem (MVT) • Constancy of functions with f 0 = 0. • Definition of increasing and decreasing on an interval. • Increasing/decreasing test • First derivative test for local ext ...
Course Code
... Equations: Elimination Methods Determinants: Evaluate 2x2 and 3x3 determinants, Using Cramer’s Rule to solve equations, Find the market equilibrium using Cramer’s Rule, Use Cramer’s Rule for the IncomeDetermination Model Matrices and Determinants, Systems of Linear Equations The Definite Integral: T ...
... Equations: Elimination Methods Determinants: Evaluate 2x2 and 3x3 determinants, Using Cramer’s Rule to solve equations, Find the market equilibrium using Cramer’s Rule, Use Cramer’s Rule for the IncomeDetermination Model Matrices and Determinants, Systems of Linear Equations The Definite Integral: T ...
MATH M25A - Moorpark College
... Find the derivatives of functions and relations using implicit differentiation. Solve applied problems using the derivative including rates of change, the tangent line problem, and related rates. Apply the method of logarithmic differentiation for finding derivatives. Solve exponential growth and de ...
... Find the derivatives of functions and relations using implicit differentiation. Solve applied problems using the derivative including rates of change, the tangent line problem, and related rates. Apply the method of logarithmic differentiation for finding derivatives. Solve exponential growth and de ...
Document
... Indefinite Integral Express f ( x)dx is called indefinite integral. It emphasizes that the result of antidifferentiation is “generic” function with a indefinite constant term “ “ is called an integral sign “f(x)” is called integrand “C” is called the constant of integration. dx is t ...
... Indefinite Integral Express f ( x)dx is called indefinite integral. It emphasizes that the result of antidifferentiation is “generic” function with a indefinite constant term “ “ is called an integral sign “f(x)” is called integrand “C” is called the constant of integration. dx is t ...
Math 1100 Practice Exam 3 23 November, 2011
... 19. Use four rectangles to approximate −1 x2 + x + 1dx. Evaluate at left-hand endpoints to determine the heights of the rectangles. ...
... 19. Use four rectangles to approximate −1 x2 + x + 1dx. Evaluate at left-hand endpoints to determine the heights of the rectangles. ...
Fundamental Theorem of Calculus, Riemann Sums, Substitution
... Notice that the integral involves one of the terms above. Substitute the appropriate u. Make sure to change the dx to a du (with relevant factor). Simplify the integral using the appropriate trig identity. Rewrite the new integral in terms of the original non-Ѳ variable (draw a reference right-trian ...
... Notice that the integral involves one of the terms above. Substitute the appropriate u. Make sure to change the dx to a du (with relevant factor). Simplify the integral using the appropriate trig identity. Rewrite the new integral in terms of the original non-Ѳ variable (draw a reference right-trian ...
15 - BrainMass
... A) Divide the coefficient by the old exponential value. B) Subtract the new exponential value from the coefficient. C) Multiply the coefficient by the new exponential value. D) Divide the coefficient by the new exponential value. ...
... A) Divide the coefficient by the old exponential value. B) Subtract the new exponential value from the coefficient. C) Multiply the coefficient by the new exponential value. D) Divide the coefficient by the new exponential value. ...
PDF
... initial guess too far out the line will generate numbers even farther out. Newton's method can't nd what doesn't exist! If f has no roots, Newton's method will try to \ nd" the function's closest approach to the x-axis; but everytime it gets close, a nearly horizontal tangent line sends it zooming ...
... initial guess too far out the line will generate numbers even farther out. Newton's method can't nd what doesn't exist! If f has no roots, Newton's method will try to \ nd" the function's closest approach to the x-axis; but everytime it gets close, a nearly horizontal tangent line sends it zooming ...
Block 5 Stochastic & Dynamic Systems Lesson 14 – Integral Calculus
... The Fundamental Theorem of Calculus Let f be a continuous real-valued function defined on a closed interval [a, b]. Let F be a function such that for all x in [a, b] then ...
... The Fundamental Theorem of Calculus Let f be a continuous real-valued function defined on a closed interval [a, b]. Let F be a function such that for all x in [a, b] then ...
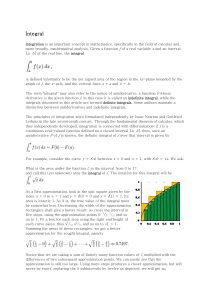
Integral
... The term "integral" may also refer to the notion of antiderivative, a function F whose derivative is the given function ƒ. In this case it is called an indefinite integral, while the integrals discussed in this article are termed definite integrals. Some authors maintain a distinction between antide ...
... The term "integral" may also refer to the notion of antiderivative, a function F whose derivative is the given function ƒ. In this case it is called an indefinite integral, while the integrals discussed in this article are termed definite integrals. Some authors maintain a distinction between antide ...









![The Fundamental Theorem of Calculus [1]](http://s1.studyres.com/store/data/020099492_1-4a7fbd2304ff84025ef2f0bc4ff924ca-300x300.png)