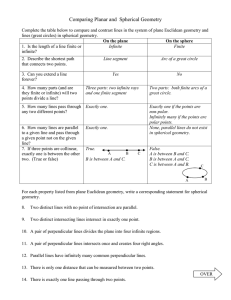
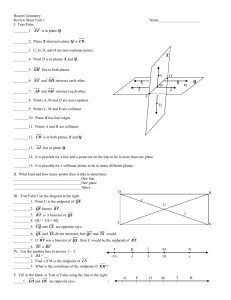
Do Now
... • Has length and width, but no thickness. • Flat surface that extends infinitely along its length and width. • Represented with a 4-sided figure, like paper. • Named with a script capital letter. ...
... • Has length and width, but no thickness. • Flat surface that extends infinitely along its length and width. • Represented with a 4-sided figure, like paper. • Named with a script capital letter. ...
2.5 Notes - APHS Mathematics
... _____________ and ___________ must intersect at C because if two line intersect, then ____________ _______________________________________________________. Point _____ is _______________ ________________ and point _____ is _________________. Points ____________________________ are __________________ ...
... _____________ and ___________ must intersect at C because if two line intersect, then ____________ _______________________________________________________. Point _____ is _______________ ________________ and point _____ is _________________. Points ____________________________ are __________________ ...
1.1 Building Blocks of Geometry
... Midpoint • Midpoint of a segment is the point on the segment that is the same distance from both endpoints – bisects the segment – divides the segment into two congruent segments ...
... Midpoint • Midpoint of a segment is the point on the segment that is the same distance from both endpoints – bisects the segment – divides the segment into two congruent segments ...
Point A - nkobersteinkhs
... You can name a line by any two points on the line. Another way to name a line is with a single lowercase letter. ...
... You can name a line by any two points on the line. Another way to name a line is with a single lowercase letter. ...
Conic section
In mathematics, a conic section (or just conic) is a curve obtained as the intersection of a cone (more precisely, a right circular conical surface) with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2, and as a quadric of dimension 1. There are a number of other geometric definitions possible. One of the most useful, in that it involves only the plane, is that a non-circular conic consists of those points whose distances to some point, called a focus, and some line, called a directrix, are in a fixed ratio, called the eccentricity.Traditionally, the three types of conic section are the hyperbola, the parabola, and the ellipse. The circle is a special case of the ellipse, and is of sufficient interest in its own right that it is sometimes called the fourth type of conic section. The type of a conic corresponds to its eccentricity, those with eccentricity less than 1 being ellipses, those with eccentricity equal to 1 being parabolas, and those with eccentricity greater than 1 being hyperbolas. In the focus-directrix definition of a conic the circle is a limiting case with eccentricity 0. In modern geometry certain degenerate cases, such as the union of two lines, are included as conics as well.The conic sections have been named and studied at least since 200 BC, when Apollonius of Perga undertook a systematic study of their properties.