10R - donnellymath
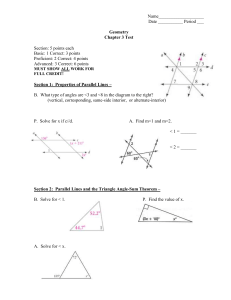
... _____3. Two lines perpendicular to the same plane are coplanar. _____4. Two planes are perpendicular to each other if and only if one plane contains a line perpendicular to the second plane. ...
... _____3. Two lines perpendicular to the same plane are coplanar. _____4. Two planes are perpendicular to each other if and only if one plane contains a line perpendicular to the second plane. ...
5. Three Dimentsinal Geometry
... intersecting lines are in the same plane. If two lines do not intersect then there is no angle between them. Angle between two lines Finding the angle between two lines in 2D is easy, just find the angle of each line with the x-axis from the slope of the line and take the difference. In 3D it is not ...
... intersecting lines are in the same plane. If two lines do not intersect then there is no angle between them. Angle between two lines Finding the angle between two lines in 2D is easy, just find the angle of each line with the x-axis from the slope of the line and take the difference. In 3D it is not ...
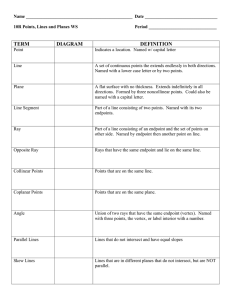
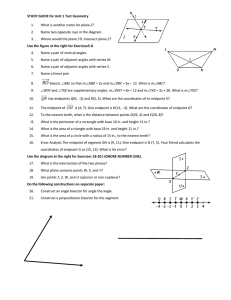
Use the first diagram to answer questions 1
... Use the second diagram to answer questions 7-12. 8. What is the intersection of plane P and plane N? 9. Which plane cannot be named with three points on the diagram? ...
... Use the second diagram to answer questions 7-12. 8. What is the intersection of plane P and plane N? 9. Which plane cannot be named with three points on the diagram? ...
POSTULATES IN GEOMETRY I-0. All lines and planes are sets of
... PS-1. The plane-Separation Postulate. Given a line and a plane containing it, the set of all points of the plane that do not lie on the line is the union of two disjoint sets such that (1) each of the sets is convex, and (2) if P belongs to one of the sets and Q belongs to the other, then the segmen ...
... PS-1. The plane-Separation Postulate. Given a line and a plane containing it, the set of all points of the plane that do not lie on the line is the union of two disjoint sets such that (1) each of the sets is convex, and (2) if P belongs to one of the sets and Q belongs to the other, then the segmen ...
Practice
... 7. Name the pair of opposite rays with endpoint N. 8. How many lines are shown in the drawing? ...
... 7. Name the pair of opposite rays with endpoint N. 8. How many lines are shown in the drawing? ...
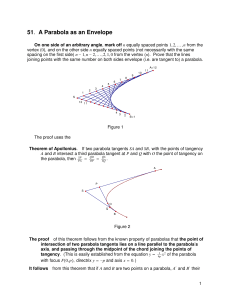
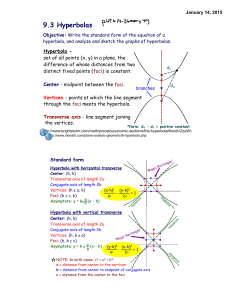
Conic section
In mathematics, a conic section (or just conic) is a curve obtained as the intersection of a cone (more precisely, a right circular conical surface) with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2, and as a quadric of dimension 1. There are a number of other geometric definitions possible. One of the most useful, in that it involves only the plane, is that a non-circular conic consists of those points whose distances to some point, called a focus, and some line, called a directrix, are in a fixed ratio, called the eccentricity.Traditionally, the three types of conic section are the hyperbola, the parabola, and the ellipse. The circle is a special case of the ellipse, and is of sufficient interest in its own right that it is sometimes called the fourth type of conic section. The type of a conic corresponds to its eccentricity, those with eccentricity less than 1 being ellipses, those with eccentricity equal to 1 being parabolas, and those with eccentricity greater than 1 being hyperbolas. In the focus-directrix definition of a conic the circle is a limiting case with eccentricity 0. In modern geometry certain degenerate cases, such as the union of two lines, are included as conics as well.The conic sections have been named and studied at least since 200 BC, when Apollonius of Perga undertook a systematic study of their properties.