Chapter 3
... Remark: In an algebraic context equivalence classes are often called cosets. For example, lines and planes in Euclidean geometry (affine subspaces) are cosets of the underlying linear algebra, the equivalence relation on the vectors being that their difference belongs to the true subspace (line or p ...
... Remark: In an algebraic context equivalence classes are often called cosets. For example, lines and planes in Euclidean geometry (affine subspaces) are cosets of the underlying linear algebra, the equivalence relation on the vectors being that their difference belongs to the true subspace (line or p ...
8 Lesson 8.1 cont
... • 3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center. ...
... • 3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center. ...
4.10 Curriculum Framework
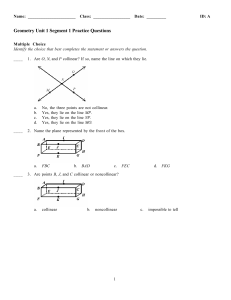
... An angle is formed by two rays that share a common endpoint called the vertex. Angles are found wherever lines or line segments intersect. An angle can be named in three different ways by using: ...
... An angle is formed by two rays that share a common endpoint called the vertex. Angles are found wherever lines or line segments intersect. An angle can be named in three different ways by using: ...
Conic section
In mathematics, a conic section (or just conic) is a curve obtained as the intersection of a cone (more precisely, a right circular conical surface) with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2, and as a quadric of dimension 1. There are a number of other geometric definitions possible. One of the most useful, in that it involves only the plane, is that a non-circular conic consists of those points whose distances to some point, called a focus, and some line, called a directrix, are in a fixed ratio, called the eccentricity.Traditionally, the three types of conic section are the hyperbola, the parabola, and the ellipse. The circle is a special case of the ellipse, and is of sufficient interest in its own right that it is sometimes called the fourth type of conic section. The type of a conic corresponds to its eccentricity, those with eccentricity less than 1 being ellipses, those with eccentricity equal to 1 being parabolas, and those with eccentricity greater than 1 being hyperbolas. In the focus-directrix definition of a conic the circle is a limiting case with eccentricity 0. In modern geometry certain degenerate cases, such as the union of two lines, are included as conics as well.The conic sections have been named and studied at least since 200 BC, when Apollonius of Perga undertook a systematic study of their properties.