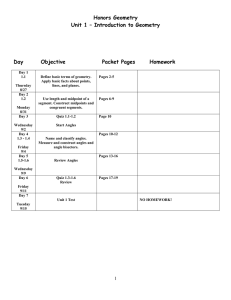
Honors Geometry
... Complete with Always, Sometimes, or Never 1. __________ Two <’s that are supplementary ___________form a linear pair. 2. __________ Two <’s that form a linear pair are ____supplementary. 3. __________Two congruent angles are _________right. 4. __________Two right angles are ___________congruent. 5. ...
... Complete with Always, Sometimes, or Never 1. __________ Two <’s that are supplementary ___________form a linear pair. 2. __________ Two <’s that form a linear pair are ____supplementary. 3. __________Two congruent angles are _________right. 4. __________Two right angles are ___________congruent. 5. ...
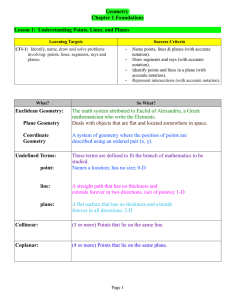
DEFINITIONS, POSTULATES, AND THEOREMS
... 30) Adjacent Angles (def)- two coplanar angles with a common side and no common interior points. 31) Intersecting Lines (def)- are coplanar and have exactly one point in common. If intersecting lines do not meet at right
... 30) Adjacent Angles (def)- two coplanar angles with a common side and no common interior points. 31) Intersecting Lines (def)- are coplanar and have exactly one point in common. If intersecting lines do not meet at right
MATH - Amazon Web Services
... The six parts of a two-column proof are listed in order: Statement: a full written statement of the theorem. Figure: a lettered figure drawn to illustrate the given conditions of the statement. Given: the given conditions of the statement expressed in terms of the letter and numerals used in the fig ...
... The six parts of a two-column proof are listed in order: Statement: a full written statement of the theorem. Figure: a lettered figure drawn to illustrate the given conditions of the statement. Given: the given conditions of the statement expressed in terms of the letter and numerals used in the fig ...
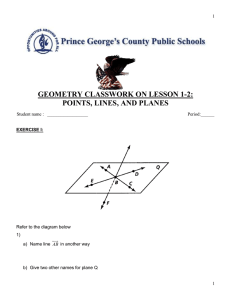
geometry classwork on lesson 1-2
... Classify each statement as TRUE or FALSE. 1. Three given points are always coplanar. 2. A line that intersects a segment at its midpoint is the perpendicular bisector. 3. The contrapositive of a true conditional is sometimes false. 4. An acute angle inscribed in a circle must intercept a minor arc. ...
... Classify each statement as TRUE or FALSE. 1. Three given points are always coplanar. 2. A line that intersects a segment at its midpoint is the perpendicular bisector. 3. The contrapositive of a true conditional is sometimes false. 4. An acute angle inscribed in a circle must intercept a minor arc. ...
Geometry - Oak Meadow
... conditional statement is equivalent to its contrapositive. Similarly, the inverse and converse of any conditional statement are equivalent. This is shown in the table above. Example 4: Writing an Inverse, Converse, and Contrapositive Write the (a) inverse, (b) converse, and (c) contrapositive of the ...
... conditional statement is equivalent to its contrapositive. Similarly, the inverse and converse of any conditional statement are equivalent. This is shown in the table above. Example 4: Writing an Inverse, Converse, and Contrapositive Write the (a) inverse, (b) converse, and (c) contrapositive of the ...
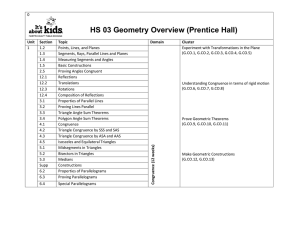
HS 03 Geometry Overview (Prentice Hall)
... Circles and Completing the Square Radii and Intercepted Arcs Introduction to Radian Measure ...
... Circles and Completing the Square Radii and Intercepted Arcs Introduction to Radian Measure ...
Conic section
In mathematics, a conic section (or just conic) is a curve obtained as the intersection of a cone (more precisely, a right circular conical surface) with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2, and as a quadric of dimension 1. There are a number of other geometric definitions possible. One of the most useful, in that it involves only the plane, is that a non-circular conic consists of those points whose distances to some point, called a focus, and some line, called a directrix, are in a fixed ratio, called the eccentricity.Traditionally, the three types of conic section are the hyperbola, the parabola, and the ellipse. The circle is a special case of the ellipse, and is of sufficient interest in its own right that it is sometimes called the fourth type of conic section. The type of a conic corresponds to its eccentricity, those with eccentricity less than 1 being ellipses, those with eccentricity equal to 1 being parabolas, and those with eccentricity greater than 1 being hyperbolas. In the focus-directrix definition of a conic the circle is a limiting case with eccentricity 0. In modern geometry certain degenerate cases, such as the union of two lines, are included as conics as well.The conic sections have been named and studied at least since 200 BC, when Apollonius of Perga undertook a systematic study of their properties.