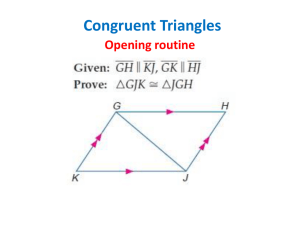
7. 5 Congruent Triangles to the Rescue
... Purpose: The purpose of this task is to provide students with practice in identifying the criteria they might use—ASA, SAS or SSS—to determine if two triangles embedded in another geometric figure are congruent, and then to use those congruent triangles to make other observations about the geome ...
... Purpose: The purpose of this task is to provide students with practice in identifying the criteria they might use—ASA, SAS or SSS—to determine if two triangles embedded in another geometric figure are congruent, and then to use those congruent triangles to make other observations about the geome ...
NYSED Associate Susan Brockley`s Geometry Common
... G.CO.C.11 Prove theorems about parallelograms (trapezoids). Theorems include: opposite sides are congruent, opposite angles are congruent, the diagonals of a parallelogram bisect each other, and conversely, rectangles are parallelograms with congruent diagonals. NYSED: Theorems include but are not l ...
... G.CO.C.11 Prove theorems about parallelograms (trapezoids). Theorems include: opposite sides are congruent, opposite angles are congruent, the diagonals of a parallelogram bisect each other, and conversely, rectangles are parallelograms with congruent diagonals. NYSED: Theorems include but are not l ...
journal5 salvador amaya 9
... _____(0-10 pts.) Describe what a perpendicular bisector is. Explain the perpendicular bisector theorem and its converse. Give 3 examples of each. _____(0-10 pts.) Describe what an angle bisector is. Explain the angle bisector theorem and its converse. Give at least 3 examples of each. _____(0-10 pt ...
... _____(0-10 pts.) Describe what a perpendicular bisector is. Explain the perpendicular bisector theorem and its converse. Give 3 examples of each. _____(0-10 pts.) Describe what an angle bisector is. Explain the angle bisector theorem and its converse. Give at least 3 examples of each. _____(0-10 pt ...
Trigonometry Unit Guide (G.SRT.5
... mathematical concepts and carry out mathematical procedures with precision and fluency. Claim 2, Problem Solving, asks students to solve a range of complex well-posed problems in pure and applied mathematics, making productive use of knowledge and problem solving strategies. Standard G.SRT.5 Use con ...
... mathematical concepts and carry out mathematical procedures with precision and fluency. Claim 2, Problem Solving, asks students to solve a range of complex well-posed problems in pure and applied mathematics, making productive use of knowledge and problem solving strategies. Standard G.SRT.5 Use con ...
Geometry Unit 5 - Mona Shores Blogs
... – GHIJ ~ KLMN • You must match the order of the second polygon with that of the first to show corresponding angles and sides! ...
... – GHIJ ~ KLMN • You must match the order of the second polygon with that of the first to show corresponding angles and sides! ...
Grade 5 Unit 5 Standards Clarification For Parents
... you will find the standards we will be learning in Unit Four. Each standard is in bold print and underlined and below it is an explanation with student examples. Your child is not learning math the way we did when we were in school, so hopefully this will assist you when you help your child at home. ...
... you will find the standards we will be learning in Unit Four. Each standard is in bold print and underlined and below it is an explanation with student examples. Your child is not learning math the way we did when we were in school, so hopefully this will assist you when you help your child at home. ...
List of Axioms and Theorems from the Second Exam Axiom A.1
... Theorem 1.9 (Hypotenuse-Leg Congruence Condition) If the hypotenuse and leg of one right triangle are congruent to the hypotenuse and leg of another right triangle, then the triangles are congruent. Theorem 1.10 (Exterior Angle Theorem) An exterior angle of a triangle is greater than either of the ...
... Theorem 1.9 (Hypotenuse-Leg Congruence Condition) If the hypotenuse and leg of one right triangle are congruent to the hypotenuse and leg of another right triangle, then the triangles are congruent. Theorem 1.10 (Exterior Angle Theorem) An exterior angle of a triangle is greater than either of the ...
1 - Rancho High School
... 61. Which of the following is not a characteristic of all parallelograms? A. Consecutive angles are supplementary B. Opposite angles are congruent ...
... 61. Which of the following is not a characteristic of all parallelograms? A. Consecutive angles are supplementary B. Opposite angles are congruent ...























