Document
... Can you guess who I am? I am a special quadrilateral. My opposite sides are parallel. I have 2 acute angles that are equal and 2 obtuse angles that are equal. I have exactly 2 lines of symmetry. All of my sides are congruent. If you cut me in half from one vertex to the opposite vertex, you would ha ...
... Can you guess who I am? I am a special quadrilateral. My opposite sides are parallel. I have 2 acute angles that are equal and 2 obtuse angles that are equal. I have exactly 2 lines of symmetry. All of my sides are congruent. If you cut me in half from one vertex to the opposite vertex, you would ha ...
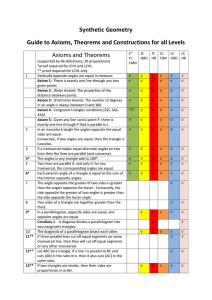
Line Pair Conjecture If two angles form a linear pair, then the
... If two parallel lines are cut by a transversal, then corresponding angles are congruent. (F-theorem) Alternate Interior Angles Conjecture If two parallel lines are cut by a transversal, then alternate interior angles are congruent. (Z-theorem) Triangle Sum The sum of the measures of the angles in ev ...
... If two parallel lines are cut by a transversal, then corresponding angles are congruent. (F-theorem) Alternate Interior Angles Conjecture If two parallel lines are cut by a transversal, then alternate interior angles are congruent. (Z-theorem) Triangle Sum The sum of the measures of the angles in ev ...