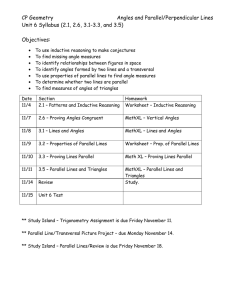
CP Geometry Angles and Parallel/Perpendicular Lines Unit 6 Syllabus
... To find missing angle measures To identify relationships between figures in space To identify angles formed by two lines and a transversal To use properties of parallel lines to find angle measures To determine whether two lines are parallel To find measures of angles of triangles ...
... To find missing angle measures To identify relationships between figures in space To identify angles formed by two lines and a transversal To use properties of parallel lines to find angle measures To determine whether two lines are parallel To find measures of angles of triangles ...
Geometry 1: Intro to Geometry Introduction to Geometry
... angles. 15. Draw a diagram that fits the following criteria: Draw two lines and a transversal such that 1 and 2 are corresponding angles, 2 and 3 are vertical angles, and 3 and 4 are corresponding angles. What type of angle pair is 1 and 4? ...
... angles. 15. Draw a diagram that fits the following criteria: Draw two lines and a transversal such that 1 and 2 are corresponding angles, 2 and 3 are vertical angles, and 3 and 4 are corresponding angles. What type of angle pair is 1 and 4? ...
Introduction ( 5 min )
... today and one item/formula that they thought was most important. Also have the student do the following: Use one of the vocabulary words from today and explain a real example from your life. Remind the students about the Parking Lot and go over any questions from the previous days Parking Lot. Also ...
... today and one item/formula that they thought was most important. Also have the student do the following: Use one of the vocabulary words from today and explain a real example from your life. Remind the students about the Parking Lot and go over any questions from the previous days Parking Lot. Also ...
Grade/Course: Geometry (First Semester) Instructional Unit 3
... those equidistant from the segment’s congruent and corresponding angles endpoints. are congruent. -Prove a theorem stating points on a perpendicular bisector of a line segment are exactly those equidistance from the segment’s endpoints. ...
... those equidistant from the segment’s congruent and corresponding angles endpoints. are congruent. -Prove a theorem stating points on a perpendicular bisector of a line segment are exactly those equidistance from the segment’s endpoints. ...