CC Investigation 4: Geometry Topics
... Students could create a table display of cross sections after you have cut these solids in different ways. Cutting solid shapes and then coloring the cuts is one way to help students understand what happens when solids are cut to make cross sections. Review the parts of a circle using a diagram. Als ...
... Students could create a table display of cross sections after you have cut these solids in different ways. Cutting solid shapes and then coloring the cuts is one way to help students understand what happens when solids are cut to make cross sections. Review the parts of a circle using a diagram. Als ...
Algebra 2B Notes
... The measure of an exterior angle of a triangle is equal to the sum of the measures of B the two nonadjacent interior angles. m 1 = m A + m B ...
... The measure of an exterior angle of a triangle is equal to the sum of the measures of B the two nonadjacent interior angles. m 1 = m A + m B ...
3 Maintaining Mathematical Proficiency Chapter
... Copyright © Big Ideas Learning, LLC All rights reserved. ...
... Copyright © Big Ideas Learning, LLC All rights reserved. ...
A diagonal - Berkeley City College
... interior angle is right. We can also try to prove that its diagonals are congruent. To prove that a parallelogram is a rhombus, we need to prove that its four sides are congruent. We can also try to prove that its diagonals are perpendicular. To prove that a parallelogram is a square, we need to pro ...
... interior angle is right. We can also try to prove that its diagonals are congruent. To prove that a parallelogram is a rhombus, we need to prove that its four sides are congruent. We can also try to prove that its diagonals are perpendicular. To prove that a parallelogram is a square, we need to pro ...
Lesson Title - Mona Shores Blogs
... Lesson Title: 5.4 Using Similar Triangles Lesson Length: 1 day HSCEs: G2.3.4, G2.3.5 Lesson Objectives: Students will be able to find the missing measurements using similar triangles. Lesson Opener: What does the term similar mean? Can a triangle have side lengths: 12, 14, 5 while another triangle ...
... Lesson Title: 5.4 Using Similar Triangles Lesson Length: 1 day HSCEs: G2.3.4, G2.3.5 Lesson Objectives: Students will be able to find the missing measurements using similar triangles. Lesson Opener: What does the term similar mean? Can a triangle have side lengths: 12, 14, 5 while another triangle ...
Warm-Up Exercises
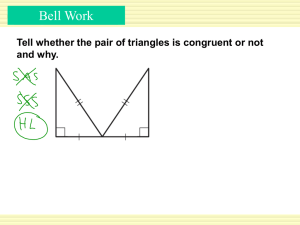
... Can the triangles be proven congruent with the information given in the diagram? If so, state the postulate or theorem you would use. ...
... Can the triangles be proven congruent with the information given in the diagram? If so, state the postulate or theorem you would use. ...
Name: Period: Unit 3 Goal Page: Triangles Unit 3 CA Standards A “T
... 2.0 Students write geometric proofs, including proofs by contradiction. 4.0 Students prove basic theorems involving congruence and similarity. 5.0 Students prove that triangles are congruent or similar, and they are able to use the concept of corresponding parts of congruent triangles. (2) 6.0 Stude ...
... 2.0 Students write geometric proofs, including proofs by contradiction. 4.0 Students prove basic theorems involving congruence and similarity. 5.0 Students prove that triangles are congruent or similar, and they are able to use the concept of corresponding parts of congruent triangles. (2) 6.0 Stude ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)