Download parallel lines - Westminster Public Schools

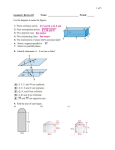
INTEGRATED I
PARALLEL LINES
SUCCESS CRITERIA:
1) Determine if lines are intersecting, parallel, or skew.
2) Use two-column proofs to justify statements regarding parallel lines.
3) Determine the value of angles formed by a transversal and parallel lines
INSTRUCTOR: Craig Sherman
Hidden Lake High School
Westminster Public Schools
PMI-NJ Center for Teaching & Learning
~1~
NJCTL.org
EMPOWER Recorded TARGET
MA.09.G.01.04
SCALE THEME
Using Coordinates to find Distance Formula
PROFICIENCY SCALE:
SCORE
4.0
3.5
REQUIREMENTS
In addition to exhibiting Score 3.0 performance, in-depth inferences and applications that go
BEYOND what was taught in class.
Score 4.0 does not equate to more work but rather a higher level of performance.
In addition to Score 3.0 performance, in-depth inferences and applications with partial success.
o Determine the appropriate solution in a Real World example.
3.0
The learner exhibits no major errors or omissions regarding any of the information and
processes (simple or complex) that were explicitly taught.
o Determine if lines are intersecting, parallel, or skew, AND
o Use two-column proofs to justify statements regarding parallel lines AND
o Determine the value of angles formed by a transversal and parallel lines
.
2.0
1.0
Can do one or more of the following skills / concepts:
There are no major errors or omissions regarding the simpler details and processes as the
learner…
o Identify if lines are intersecting, parallel, or skew, OR
o Identify the pairs of angle formed by parallel lines cut by a transversal, OR
o Determine the value of a linear pair of angles, OR
o Determine the value of a linear pair of angles, OR
o Determine the value of alternate interior angle, OR
o Determine the value of alternate exterior angles, OR
o Determine the value of vertical angles, OR
o Determine the value of corresponding angles, OR
o Prove statements about parallel lines using two-column proofs
Know and use the vocabulary
Identify the Basic Elements
With help, a partial understanding of some of the simpler details and process
PMI-NJ Center for Teaching & Learning
~2~
NJCTL.org
LINES: Intersecting, Parallel & Skew
WORD or CONCEPT
DEFINITION or NOTES
EXAMPLE or GRAPHIC REPRESENTATION
intersecting
parallel
skew
coplanar
INSTRUCTION 1: KHAN ACADEMY
Geometry: Parallel Lines
INSTRUCTION 2: SOPHIA
~3~
NJCTL.org
Class Work – Use image 1
1.
2.
3.
4.
5.
̅̅̅̅:
Name all segments parallel to 𝐺𝐻
̅̅̅̅
Name all segments skew to 𝐺𝐻 :
̅̅̅̅:
Name all segments intersecting with 𝐺𝐻
̅̅̅̅
̅̅̅̅
Are segments 𝐺𝐻 and 𝐵𝐴 coplanar? Explain your answer.
Are segments ̅̅̅̅
𝐺𝐻 and ̅̅̅̅
𝐵𝐹 coplanar? Explain your answer.
Is each statement true always, sometimes, or never?
6. Two intersecting lines are skew.
7. Two parallel lines are coplanar.
8. Two lines in the same plane are parallel.
9. Two lines that do not intersect are parallel.
10. Two skew lines are coplanar
Image 1
Homework - Use Image 1
11.
12.
13.
14.
15.
̅̅̅̅ :
Name all segments parallel to 𝐹𝐸
̅̅̅̅
Name all segments skew to 𝐹𝐸 :
̅̅̅̅ :
Name all segments intersecting with 𝐹𝐸
̅̅̅̅
̅̅̅̅
Are segments 𝐹𝐸 and 𝐶𝐷coplanar? Explain your answer.
Are segments ̅̅̅̅
𝐹𝐸 and ̅̅̅̅
𝐻𝐷 coplanar? Explain your answer.
State whether the following statements are always, sometimes, or never true:
16. Two coplanar lines are skew.
17. Two intersecting lines are in the same plane.
18. Two lines in the same plane are parallel.
Geometry: Parallel Lines
~4~
NJCTL.org
Lines & Transversals
WORD or CONCEPT
DEFINITION or NOTES
EXAMPLE or GRAPHIC REPRESENTATION
parallel lines
transversal
same side interior
angles
same side exterior
angles
corresponding angles
alternate interior
angles
alternate exterior
angles
INSTRUCTION 1: KHAN ACADEMY
Geometry: Parallel Lines
INSTRUCTION 2: SOPHIA
~5~
NJCTL.org
Class Work
Classify each pair of angles as alternate interior, alternate exterior, same-side interior, same-side exterior,
corresponding angles, or none of these.
19. ∠11 and ∠16 are
20. ∠12 and ∠2 are
21. ∠14 and ∠8 are
22. ∠6 and ∠16 are
23. ∠7 and ∠14 are
24. ∠3 and ∠16 are
Homework
Classify each pair of angles as alternate interior, alternate exterior, same-side interior, same-side exterior,
corresponding angles, or none of these.
25. ∠7 and ∠12
26. ∠3 and ∠6
27. ∠6 and ∠11
28. ∠7 and ∠11
29. ∠4 and ∠10
30. ∠14 and ∠16
31. ∠2 and ∠3
32. ∠2 and ∠10
Geometry: Parallel Lines
~6~
NJCTL.org
Parallel Lines & Proofs
WORD or CONCEPT
DEFINITION or NOTES
EXAMPLE or GRAPHIC REPRESENTATION
proof
statement
reason
substitution
transitive property
reflexive property
symmetric property
INSTRUCTION 1: KHAN ACADEMY
Geometry: Parallel Lines
INSTRUCTION 2: SOPHIA
~7~
NJCTL.org
Classwork
Match each expression/equation with the property used to make the conclusion.
33.
AB = AB
34.
If m∠A = m∠B and m∠B = m∠C, then m∠A = m∠C.
35.
If x + y = 9 and y = 5, then x + 5 = 9.
36.
If DE = FG, then FG = DE.
a)
b)
c)
d)
Substitution Property of Equality
Transitive Property of Equality
Reflexive Property of Equality
Symmetric Property of Equality
PARCC type question:
37.
Alternate Exterior Angles Proof: Complete the proof by filling in the missing reasons
with the “reasons bank” below.
Given: line m || line k
Prove: ∠2 ≅ ∠8
Statements
1. line m || line k
2. ∠2 ≅ ∠6
Reasons
1.
2.
3. ∠6 ≅ ∠8
3.
4. ∠2 ≅ ∠8
4.
Reasons Bank
a) Transitive Property of Congruence
b) If 2 parallel lines are cut by a
transversal, then the corresponding
angles are congruent.
c) Vertical Angles are congruent.
d) Given
Geometry: Parallel Lines
~8~
NJCTL.org
Homework
For #39-42 match the description on the left to the name of the property on the right.
38.
∠A ≅ ∠B and ∠B ≅ ∠C, then ∠A ≅ ∠C. a) Substitution Property of Equality
39.
If bc = 77 and b = 11, then 11c = 77.
b) Transitive Property of Congruence
40.
If ∠P ≅ ∠M, then ∠M ≅ ∠P.
c) Reflexive Property of Equality
41.
QR = QR
d) Symmetric Property of Congruence
PARCC type question:
42.
Alternate Interior Angles Proof: Complete the proof by filling in the missing reasons
with the “reasons bank” below.
Given: line m || line k
Prove: ∠3 ≅ ∠5
Statements
1. line m || line k
2. ∠3 ≅ ∠7
3. ∠7 ≅ ∠5
4. ∠3 ≅ ∠5
a)
b)
c)
d)
Reasons
1.
2.
3.
4.
Reasons Bank
Vertical Angles are congruent.
Given
Transitive Property of Congruence
If 2 parallel lines are cut by a transversal,
then the corresponding angles are
congruent.
Geometry: Parallel Lines
~9~
NJCTL.org
Properties of Parallel Lines
Classwork
Use the given diagram to answer problems #33-41.
43.
44.
45.
46.
47.
If m∠9 = 54°, then find the measure the following angles:
m∠1=
m∠2=
m∠4=
m∠5=
m∠15=
If m∠2 = (12x-54)° and m∠10 = (7x+26)°, then find the measure the following angles:
50.m∠6=
51. m∠11=
52. m∠9=
53. m∠16=
Find the values of the unknown variables in each figure.
54.
56.
State which segments (if any) are parallel.
56.
57.
Solve for the unknowns
58.
Geometry: Parallel Lines
~10~
NJCTL.org
Homework
If m∠9 = 62°, then find the measure the following angles:
59. m∠1=
60.m∠2=
61.m∠4=
62.m∠5=
63m∠15=
If m ∠2 = (14x-24)° and m ∠10 = (6x+72)°, then find the measure the following angles:
64.m∠6=
65m∠11=
66m∠9=
67.m∠16=
Find the values of the unknown variables in each figure. (#78-82)
68.
69.
State which segments (if any) are parallel.
70
D
71. .
C
124°
124°
A
B
72.
Geometry: Parallel Lines
~11~
NJCTL.org
PARALLEL LINE SUMMARY
ANGLES
ADJACENT
LINEAR PAIR
SAME SIDE
INTERIOR
EXTERIOR
ALTERNATE
VERTICAL
CORRESPONDING
1-int
1-ext
INTERIOR
CONGRUENT (
Supplementary
Def of suppl
+
Geometry: Parallel Lines
EXTERIOR
Def of
=
≅)
≅
=
180
~12~
NJCTL.org
Parallel Lines
UNIT Review
Multiple Choice
1. Name the segment parallel to ̅̅̅̅
𝐺𝐻 and skew to ̅̅̅̅
𝐸𝐴.
̅̅̅̅
a. 𝐹𝐵
b. ̅̅̅̅
𝐷𝐴
̅
c. 𝐽𝐼
̅̅̅̅
d. 𝐻𝐷
̅̅̅̅ and skew to 𝐸𝐼.
̅̅̅̅
2. Name the segment parallel to 𝐵𝐶
̅̅̅̅
a. 𝐹𝐵
̅̅̅̅
b. 𝐷𝐴
̅
c. 𝐽𝐼
d. ̅̅̅̅
𝐻𝐷
3. Determine if the statement is always, sometimes, or never true:
Two skew lines are coplanar.
a. Always
b. Sometimes
c. Never
4. Determine if the statement is always, sometimes, or never true:
Two intersecting lines are coplanar
a. Always
b. Sometimes
c. Never
5. Determine if the statement is always, sometimes, or never true:
Two lines that do not intersect are skew.
a. Always
b. Sometimes
c. Never
6. Determine the relationship between ∠1 & ∠10.
a. Alternate Interior
b. Same-side Interior
c. Corresponding Angles
d. None of these
7. Determine the relationship between ∠5 & ∠15.
a. Alternate Exterior
b. Alternate Interior
c. Same-side Interior
d. None of these
Geometry: Parallel Lines
~13~
NJCTL.org
8. Given in the diagram to the right, m∠2=3x-10 and m∠15=2x+30 , what is m∠12?
a. 32o
b. 40o
c. 86o
d. 110o
9. Given in the diagram to the right, m∠5=
(7x+2)°and m∠11=(5x+14)°, what is
a. 6°
b. 44°
c. 46°
d. 136°
m∠14?
In 10-11, use the diagram at the right.
10. Given ∠2 ≅ ∠6, what justifies k || m.
a. Converse Alternate Interior Angles
Theorem
b. Converse Alternate Exterior Angles Theorem
c. Converse Corresponding Angles Theorem
d. there is not enough info to state parallel
11. Given n || p , what justifies ∠1 ≅ ∠12
a. Alternate Interior Angles Theorem
b. Alternate Exterior Angles Theorem
c. Corresponding Angles Theorem
d. there is not enough info to make this statement
Geometry: Parallel Lines
~14~
NJCTL.org
Extended Constructed Response
1. Complete the proof by filling in the missing reasons
“reasons bank” to the right. Some reasons may be
more that once.
̅̅̅̅
̅̅̅̅̅ || 𝑃𝑄
Given: ∠1 ≅ ∠3; 𝑀𝑁
Prove: ∠2≅∠3
M
N
1
3
2
P
Statements
1. ∠1 ≅ ∠3
2. ̅̅̅̅̅
𝑀𝑁 || ̅̅̅̅
𝑃𝑄
3. ∠1 ≅ ∠2
4. ∠2≅∠3
Reasons
1.
2.
3.
4.
with the
used
Q
Reasons Bank
a) Transitive Property of Congruence
b) If 2 parallel lines are cut by a
transversal, then the alternate interior angles
are congruent.
c) Given
2. Complete the proof by filling in the missing reasons with the “reasons bank” to the right. Some
reasons may be used more that once.
Given: n || p, k || m
Prove: ∠2 & ∠13 are supplementary
Statements
1. n || p, k || m
2. ∠2 ≅ ∠12
3. ∠12 ≅ ∠14
4. ∠2 ≅ ∠14
5. m∠2 = m∠14
6. m∠13 & m∠14 are
supplementary
7. m∠13 + m∠14 = 180°
8. m∠13 + m∠2 = 180°
9. ∠2 &∠13 are supplementary
Reasons
1.
2.
3.
4.
5.
6.
7.
8.
9.
Reasons Bank
a) Transitive Property of Congruence
b) Definition of supplementary angles
c) If 2 parallel lines are cut by a transversal, then the alternate interior
angles are congruent.
d) Definition of Congruent Angles
e) Given
f) If 2 parallel lines are cut by a transversal, then the alternate exterior
angles are congruent.
g) Angles that form a linear pair are supplementary
h) Substitution Property of Equality
Geometry: Parallel Lines
~15~
NJCTL.org