MAFS Geo EOC Review Congruency Similarity and Right Triangles
... FSA Geometry EOC Review Table of Contents MAFS.912.G-CO.1.1 EOC Practice ........................................................................................................................................... 3 MAFS.912.G-CO.1.2 EOC Practice ..................................................... ...
... FSA Geometry EOC Review Table of Contents MAFS.912.G-CO.1.1 EOC Practice ........................................................................................................................................... 3 MAFS.912.G-CO.1.2 EOC Practice ..................................................... ...
SYNTHETIC PROJECTIVE GEOMETRY
... not lie on L, and assume that M1 , · · · Mk are lines which pass through X and meet L in points Y1 , · · · Yk respectively. Prove that the points Y 1 , · · · Yk are distinct if and only if the lines M1 , · · · Mk are distinct. 5. Let (S, Π, d) be a regular incidence space of dimension ≥ 3, and assum ...
... not lie on L, and assume that M1 , · · · Mk are lines which pass through X and meet L in points Y1 , · · · Yk respectively. Prove that the points Y 1 , · · · Yk are distinct if and only if the lines M1 , · · · Mk are distinct. 5. Let (S, Π, d) be a regular incidence space of dimension ≥ 3, and assum ...
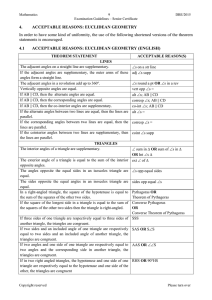
Slope
... Suppose you were given the following question on your exam: A line contains the points (3,4) and (5,8). What is the slope of the line? To solve this problem, we will use our formula for finding slope. Now, you could graph these two points on a coordinate system, draw the line that connects them and ...
... Suppose you were given the following question on your exam: A line contains the points (3,4) and (5,8). What is the slope of the line? To solve this problem, we will use our formula for finding slope. Now, you could graph these two points on a coordinate system, draw the line that connects them and ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)