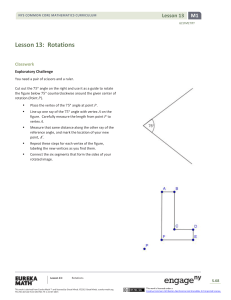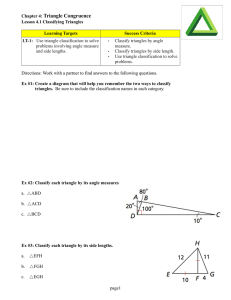
2015 Geometry Curriculum Map
... 4-4: Using Corresponding Parts of Congruent Triangles G.CO.1. Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. G-CO.9. Prove theorems about lines a ...
... 4-4: Using Corresponding Parts of Congruent Triangles G.CO.1. Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. G-CO.9. Prove theorems about lines a ...
Overview - Connecticut Core Standards
... other, then flip it over. Show that, keeping vertex A at the same place, you can make vertex B on one triangle coincide with vertex C on the other and vice versa. At the end of the first day you may give students Exit Slip 2.3.1, which is based on Activity ...
... other, then flip it over. Show that, keeping vertex A at the same place, you can make vertex B on one triangle coincide with vertex C on the other and vice versa. At the end of the first day you may give students Exit Slip 2.3.1, which is based on Activity ...
Geometry - ANSWER KEY DAY 1 1. D. 2. 3. Some
... Correct response—any obtuse angle Correct #2 Any closed figure that contains at least one obtuse angle. The obtuse angle does not need to be designated Incorrect Any incorrect response—includes straight line with no vertex indicated In this question the student was asked to draw an angle that is lar ...
... Correct response—any obtuse angle Correct #2 Any closed figure that contains at least one obtuse angle. The obtuse angle does not need to be designated Incorrect Any incorrect response—includes straight line with no vertex indicated In this question the student was asked to draw an angle that is lar ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)