PROPERTIES For any numbers a, b, c, and d: (Arithmetic) 1
... 3. Segment Duplication Postulate: You can construct a segment congruent to another segment. 4. Angle Duplication Postulate You can construct an angle congruent to another angle. 5. Midpoint Postulate: You can construct exactly one midpoint on any line segment. 6. Angle Bisector Postulate: You can co ...
... 3. Segment Duplication Postulate: You can construct a segment congruent to another segment. 4. Angle Duplication Postulate You can construct an angle congruent to another angle. 5. Midpoint Postulate: You can construct exactly one midpoint on any line segment. 6. Angle Bisector Postulate: You can co ...
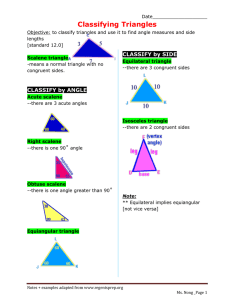
Congruent Triangles (part 1)
... If two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent. ...
... If two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent. ...
January 17, 2017 - Ottawa Hills Local Schools
... If corresponding side lengths in two triangles are proportional, then the triangles are similar. F C A ...
... If corresponding side lengths in two triangles are proportional, then the triangles are similar. F C A ...
MLI final Project-Ping
... What Have We Learned about Regularity from the Platonic Solids? No other figure, besides the said five figures, can be constructed by equilateral and equiangular figures equal to one another. ( a proposition have been appended by Euclid possibly in Book XI of the Elements) ...
... What Have We Learned about Regularity from the Platonic Solids? No other figure, besides the said five figures, can be constructed by equilateral and equiangular figures equal to one another. ( a proposition have been appended by Euclid possibly in Book XI of the Elements) ...
Similar Triangles - Peoria Public Schools
... 1) The student will learn proportional relationships ...
... 1) The student will learn proportional relationships ...
PDF version - Rice University
... What Have We Learned about Regularity from the Platonic Solids? No other figure, besides the said five figures, can be constructed by equilateral and equiangular figures equal to one another. ( a proposition have been appended by Euclid possibly in Book XI of the Elements) ...
... What Have We Learned about Regularity from the Platonic Solids? No other figure, besides the said five figures, can be constructed by equilateral and equiangular figures equal to one another. ( a proposition have been appended by Euclid possibly in Book XI of the Elements) ...
5.2-5.4, 6.2 - rosenmath.com
... nonincluded If two angles and a _____________________ side of one congruent to two angles and the triangle are _______________ nonincluded corresponding ____________________ side of a second congruent triangle, then the two triangles are ________________. ...
... nonincluded If two angles and a _____________________ side of one congruent to two angles and the triangle are _______________ nonincluded corresponding ____________________ side of a second congruent triangle, then the two triangles are ________________. ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)