Geometry Summer Institute 2014 Parallel Lines and Angles
... Having learned what it means for two geometric figures to be congruent, participants now get to see some immediate applications. Since we are already in possession of all the general criteria for triangle congruence, we are free to develop some of the concept on geometry at this point as in the clas ...
... Having learned what it means for two geometric figures to be congruent, participants now get to see some immediate applications. Since we are already in possession of all the general criteria for triangle congruence, we are free to develop some of the concept on geometry at this point as in the clas ...
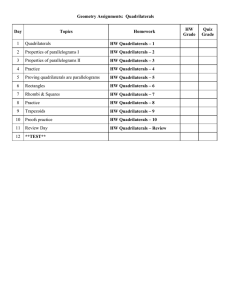
1 st 9 weeks 2014 – 2015 (Subject to Change)
... Obj: Apply Pythagorean Theorem to find the distance between two points on the coordinate plane. Develop the midpoint formula. Emphasize that the midpoint is the “average” of the endpoints. HW: Page 56 #3-9 odd; 10-17 all; 19-31 odd; 41-43, 45, 48 (change directions so that answers are exact, not nea ...
... Obj: Apply Pythagorean Theorem to find the distance between two points on the coordinate plane. Develop the midpoint formula. Emphasize that the midpoint is the “average” of the endpoints. HW: Page 56 #3-9 odd; 10-17 all; 19-31 odd; 41-43, 45, 48 (change directions so that answers are exact, not nea ...
Introducing Geometry
... phrase. However, it is impossible to define point, line, and plane without using words or phrases that themselves need definition. So these terms remain undefined. Yet, they are the basis for all of geometry. Using the undefined terms point, line, and plane, you can define all other geometry terms a ...
... phrase. However, it is impossible to define point, line, and plane without using words or phrases that themselves need definition. So these terms remain undefined. Yet, they are the basis for all of geometry. Using the undefined terms point, line, and plane, you can define all other geometry terms a ...
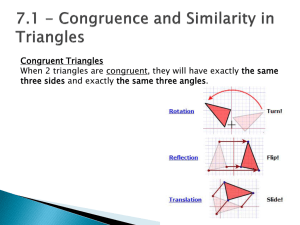
7.1 - Congruence and Similarity in Triangles
... If two triangles are congruent, then they are also similar If two triangles are similar, they are not always congruent If two pairs of corresponding angles in two triangles are equal, then the triangles are similar If in addition two corresponding sides are equal, then the triangles are congruent ...
... If two triangles are congruent, then they are also similar If two triangles are similar, they are not always congruent If two pairs of corresponding angles in two triangles are equal, then the triangles are similar If in addition two corresponding sides are equal, then the triangles are congruent ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)