Polymers composed of a large number of repeating units. Isomers
... An edge dislocation is a defect where an extra half-plane of atoms is introduced mid way through the crystal, distorting nearby planes of atoms. A screw dislocation is much harder to visualize. Imagine cutting a crystal along a plane and slipping one half across the other by a lattice vector, the h ...
... An edge dislocation is a defect where an extra half-plane of atoms is introduced mid way through the crystal, distorting nearby planes of atoms. A screw dislocation is much harder to visualize. Imagine cutting a crystal along a plane and slipping one half across the other by a lattice vector, the h ...
19.1-forces-within-Earth
... plates, rocks in the crust often resist movement. Over time stress builds up. Stress is the total force acting on crustal rocks per unit of area. When stress overcomes the strength of the rock, movement occurs along the fractures in the rock. The vibrations caused by this sudden movement are felt as ...
... plates, rocks in the crust often resist movement. Over time stress builds up. Stress is the total force acting on crustal rocks per unit of area. When stress overcomes the strength of the rock, movement occurs along the fractures in the rock. The vibrations caused by this sudden movement are felt as ...
Fluids - Northern Illinois University
... A change in a property like pressure depends on the view. In a Lagrangian view the total time derivative depends on position and time. An Eulerian view is just the partial derivative with time. • Points are fixed ...
... A change in a property like pressure depends on the view. In a Lagrangian view the total time derivative depends on position and time. An Eulerian view is just the partial derivative with time. • Points are fixed ...
PSE4_Lecture_Ch12
... This proportionality holds until the force reaches the proportional limit. Beyond that, the object will still return to its original shape up to the elastic limit. Beyond the elastic limit, the material is permanently deformed, and it breaks at the breaking point. ...
... This proportionality holds until the force reaches the proportional limit. Beyond that, the object will still return to its original shape up to the elastic limit. Beyond the elastic limit, the material is permanently deformed, and it breaks at the breaking point. ...
HW1
... known for each of the two orientations shown in Fig. P1.35. Using Mohr’s circle, determine the following stress components: (a) xy, and (b)x’y’, and y’. ...
... known for each of the two orientations shown in Fig. P1.35. Using Mohr’s circle, determine the following stress components: (a) xy, and (b)x’y’, and y’. ...
Simplified Thermal Stress Analysis
... help reduce stress. However, these voids will increase thermal resistance, increasing the junction temp, so this may not be a good thing. Also, watch out for stress concentrations, such as those caused by large voids. Use compliant bonding materials, such as soft solders and soft epoxies. Pb-Sn sold ...
... help reduce stress. However, these voids will increase thermal resistance, increasing the junction temp, so this may not be a good thing. Also, watch out for stress concentrations, such as those caused by large voids. Use compliant bonding materials, such as soft solders and soft epoxies. Pb-Sn sold ...
Lecture 8a - States of Matter
... The change in length of a stretched object depends not only on the applied force, but also on its length, cross-sectional area and the material from which it is made. The material factor, E, is called the elastic modulus or Young’s modulus, and it has been measured for many materials. ...
... The change in length of a stretched object depends not only on the applied force, but also on its length, cross-sectional area and the material from which it is made. The material factor, E, is called the elastic modulus or Young’s modulus, and it has been measured for many materials. ...
Project_FEA.doc
... Governing Equation: The Anand Model In ANSYS there are various models available to simulate visco-plasticity. The Anand model was originally developed for metal forming applications. It is however applicable to applications that involve strain and temperature effect including solder joints and hig ...
... Governing Equation: The Anand Model In ANSYS there are various models available to simulate visco-plasticity. The Anand model was originally developed for metal forming applications. It is however applicable to applications that involve strain and temperature effect including solder joints and hig ...
R-29_ChenYQ.pdf
... material, in which different local failure models are defined for different structures and materials to describe the failure of structure joint or material element. A two-parameter Weibull distribution is employed to produce the initial heterogeneity of material, i.e., the Young modulus and the fail ...
... material, in which different local failure models are defined for different structures and materials to describe the failure of structure joint or material element. A two-parameter Weibull distribution is employed to produce the initial heterogeneity of material, i.e., the Young modulus and the fail ...
Concepts of stress and strain
... Approximate by the area under the stress-strain curve Engineering tensile stress, σ ...
... Approximate by the area under the stress-strain curve Engineering tensile stress, σ ...
Tensile Testing
... STRENGTH - the greatest stress that the material can withstand prior to failure. DUCTILITY - a material property that allows it to undergo considerable plastic deformation under a load before failure. ELASTICITY - a material property that allows it to retain its original dimensions after removal of ...
... STRENGTH - the greatest stress that the material can withstand prior to failure. DUCTILITY - a material property that allows it to undergo considerable plastic deformation under a load before failure. ELASTICITY - a material property that allows it to retain its original dimensions after removal of ...
MATERIALS
... A. Elastic--for most materials and for small deformations, loading and unloading returns material to original length--can be done repeatedly, e.g., a watch spring. B. Plastic--larger deformations are not reversible when "elastic limit" is exceeded. Some materials are almost purely plastic, e.g., put ...
... A. Elastic--for most materials and for small deformations, loading and unloading returns material to original length--can be done repeatedly, e.g., a watch spring. B. Plastic--larger deformations are not reversible when "elastic limit" is exceeded. Some materials are almost purely plastic, e.g., put ...
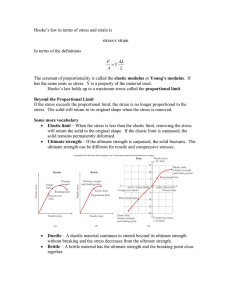
Hooke`s law in terms of stress and strain is strain stress∝ In terms of
... Hooke’s law holds up to a maximum stress called the proportional limit. Beyond the Proportional Limit If the stress exceeds the proportional limit, the strain is no longer proportional to the stress. The solid will return to its original shape when the stress is removed. Some more vocabulary Elast ...
... Hooke’s law holds up to a maximum stress called the proportional limit. Beyond the Proportional Limit If the stress exceeds the proportional limit, the strain is no longer proportional to the stress. The solid will return to its original shape when the stress is removed. Some more vocabulary Elast ...
High Strain Mechanics and Its Importance in Crushing and Grinding
... stonework fragmented due to the massive explosion. Brittle materials behave differently when subjected to high strain rates as opposed to quasistatic strain rates. Quasi-static loading occurs when the stress pulse is slow enough for the system to remain in internal equilibrium. That is, material fra ...
... stonework fragmented due to the massive explosion. Brittle materials behave differently when subjected to high strain rates as opposed to quasistatic strain rates. Quasi-static loading occurs when the stress pulse is slow enough for the system to remain in internal equilibrium. That is, material fra ...
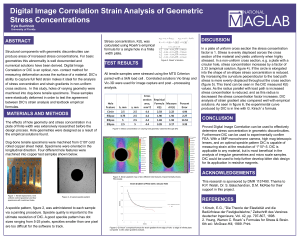
Digital Image Correlation Strain Analysis of Geometric Stress
... By increasing the curvature perpendicular to the load path stress is more evenly displaced throughout the cross section (figure 5). This trend can be seen in the DIC measured K(t) values. As the radius parallel with load path is increased stress concentration is reduced, and as this radius is decrea ...
... By increasing the curvature perpendicular to the load path stress is more evenly displaced throughout the cross section (figure 5). This trend can be seen in the DIC measured K(t) values. As the radius parallel with load path is increased stress concentration is reduced, and as this radius is decrea ...
Metamorphic Fabric Solid-state Crystal Growth Nucleation
... – Linear deformation with applied stress • Viscous (honey) – No deformation recoverable – No threshold for deformation ...
... – Linear deformation with applied stress • Viscous (honey) – No deformation recoverable – No threshold for deformation ...
Viscoplasticity
Viscoplasticity is a theory in continuum mechanics that describes the rate-dependent inelastic behavior of solids. Rate-dependence in this context means that the deformation of the material depends on the rate at which loads are applied. The inelastic behavior that is the subject of viscoplasticity is plastic deformation which means that the material undergoes unrecoverable deformations when a load level is reached. Rate-dependent plasticity is important for transient plasticity calculations. The main difference between rate-independent plastic and viscoplastic material models is that the latter exhibit not only permanent deformations after the application of loads but continue to undergo a creep flow as a function of time under the influence of the applied load.The elastic response of viscoplastic materials can be represented in one-dimension by Hookean spring elements. Rate-dependence can be represented by nonlinear dashpot elements in a manner similar to viscoelasticity. Plasticity can be accounted for by adding sliding frictional elements as shown in Figure 1. In the figure E is the modulus of elasticity, λ is the viscosity parameter and N is a power-law type parameter that represents non-linear dashpot [σ(dε/dt)= σ = λ(dε/dt)(1/N)]. The sliding element can have a yield stress (σy) that is strain rate dependent, or even constant, as shown in Figure 1c.Viscoplasticity is usually modeled in three-dimensions using overstress models of the Perzyna or Duvaut-Lions types. In these models, the stress is allowed to increase beyond the rate-independent yield surface upon application of a load and then allowed to relax back to the yield surface over time. The yield surface is usually assumed not to be rate-dependent in such models. An alternative approach is to add a strain rate dependence to the yield stress and use the techniques of rate independent plasticity to calculate the response of a materialFor metals and alloys, viscoplasticity is the macroscopic behavior caused by a mechanism linked to the movement of dislocations in grains, with superposed effects of inter-crystalline gliding. The mechanism usually becomes dominant at temperatures greater than approximately one third of the absolute melting temperature. However, certain alloys exhibit viscoplasticity at room temperature (300K). For polymers, wood, and bitumen, the theory of viscoplasticity is required to describe behavior beyond the limit of elasticity or viscoelasticity. In general, viscoplasticity theories are useful in areas such as the calculation of permanent deformations, the prediction of the plastic collapse of structures, the investigation of stability, crash simulations, systems exposed to high temperatures such as turbines in engines, e.g. a power plant, dynamic problems and systems exposed to high strain rates.↑ ↑ ↑ ↑