Eng
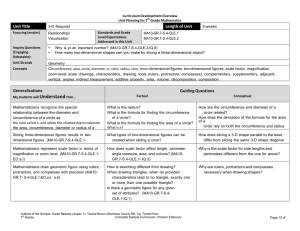
... Bases of a Prism: The two faces formed by congruent polygons that lie in parallel planes, all of the other faces being parallelograms. Cubic Units: Volume of the solids is measured in Cubic Units. Edge: The intersection of a pair of faces in a three-dimensional figure. Equilateral Triangle: A triang ...
... Bases of a Prism: The two faces formed by congruent polygons that lie in parallel planes, all of the other faces being parallelograms. Cubic Units: Volume of the solids is measured in Cubic Units. Edge: The intersection of a pair of faces in a three-dimensional figure. Equilateral Triangle: A triang ...
Geometry
... congruent figures, describe a sequence that exhibits the congruence between them. Standard 8.G.3 Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates. Standard 8.G.4 Understand that a two-dimensional figure is similar to another if t ...
... congruent figures, describe a sequence that exhibits the congruence between them. Standard 8.G.3 Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates. Standard 8.G.4 Understand that a two-dimensional figure is similar to another if t ...
Part I Linear Spaces
... f these sequences should converge to a limit, although two different Inside the new space M sequences may have the same limit. The idea is to identify these sequences together using f from there. some equivalence relation and build M More specifcally, for two Cauchy sequences x = (xn ) and y = (yn ) ...
... f these sequences should converge to a limit, although two different Inside the new space M sequences may have the same limit. The idea is to identify these sequences together using f from there. some equivalence relation and build M More specifcally, for two Cauchy sequences x = (xn ) and y = (yn ) ...
1. The following figure is a box in which the top and bottom are
... 10. A student claims that if any two planes that do not intersect are parallel, then any two lines that do not intersect should also be parallel. How do you respond? No, it’s possible for two lines to be skew in three dimensions. In three dimensions, planes (2D objects) that do not intersect must be ...
... 10. A student claims that if any two planes that do not intersect are parallel, then any two lines that do not intersect should also be parallel. How do you respond? No, it’s possible for two lines to be skew in three dimensions. In three dimensions, planes (2D objects) that do not intersect must be ...
CIS 736 (Computer Graphics) Lecture 1 of 30 - KDD
... Some Basic Analytic Geometry and Linear Algebra for CG – Vector space (VS) – collection of vectors admitting addition, scalar multiplication and observing VS axioms – Affine space (AS) – collection of points with associated vector space admitting vector difference, point-vector addition and observin ...
... Some Basic Analytic Geometry and Linear Algebra for CG – Vector space (VS) – collection of vectors admitting addition, scalar multiplication and observing VS axioms – Affine space (AS) – collection of points with associated vector space admitting vector difference, point-vector addition and observin ...
On Euclidean and Non-Euclidean Geometry by Hukum Singh DESM
... namely “The Elements”. This book was written by Euclid in about 300 B.C. The book consisted 13 volumes. The first six volumes consisted study of geometry, seven to ten consisted number theory and last three consisted three dimensional solid geometry. The Euclid axioms are [1], [3] (a)There lie infin ...
... namely “The Elements”. This book was written by Euclid in about 300 B.C. The book consisted 13 volumes. The first six volumes consisted study of geometry, seven to ten consisted number theory and last three consisted three dimensional solid geometry. The Euclid axioms are [1], [3] (a)There lie infin ...
Geometry
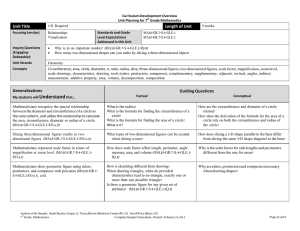
... perpendicular lines using a straight edge and compass or a drawing program, explaining and justifying the process used. ...
... perpendicular lines using a straight edge and compass or a drawing program, explaining and justifying the process used. ...
SLV RT3 - 3-D Required
... Use facts about supplementary, complementary, vertical, and adjacent angles in a multi-step problem to write and solve simple equations for an unknown angle in a figure. (MA10-GR.7-S.4-GLE.2-EO.c) ...
... Use facts about supplementary, complementary, vertical, and adjacent angles in a multi-step problem to write and solve simple equations for an unknown angle in a figure. (MA10-GR.7-S.4-GLE.2-EO.c) ...
Flatland 2: Sphereland
... coming out larger than 180◦ . This is because Flatland turned out to be the surface of a sphere. In spherical geometry, lines are great circles; circles which cut a sphere into two identical hemispheres. A triangle in spherical geometry is formed by three great circles; the sum of the angles can var ...
... coming out larger than 180◦ . This is because Flatland turned out to be the surface of a sphere. In spherical geometry, lines are great circles; circles which cut a sphere into two identical hemispheres. A triangle in spherical geometry is formed by three great circles; the sum of the angles can var ...
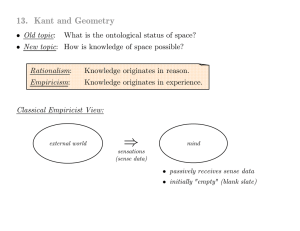
13.Kant and Geometry
... "Space is a necessary a priori representation, which underlies all outer intuitions. We can never represent to ourselves the absence of space, though we can quite well think it as empty of objects. It must therefore be regarded as the condition of the possibility of appearances, and not as a determi ...
... "Space is a necessary a priori representation, which underlies all outer intuitions. We can never represent to ourselves the absence of space, though we can quite well think it as empty of objects. It must therefore be regarded as the condition of the possibility of appearances, and not as a determi ...
Geometry - Tools for the Common Core Standards
... 3 Recognize a line of symmetry for a two-dimensional figure as a line across the figure such that the figure can be folded along the line into matching parts. Identify line-symmetric figures and draw lines of symmetry. ...
... 3 Recognize a line of symmetry for a two-dimensional figure as a line across the figure such that the figure can be folded along the line into matching parts. Identify line-symmetric figures and draw lines of symmetry. ...
the group exercise in class on Monday March 28
... 5. Remove one of these lines and keep the other. Now choose a point not on that line. How many lines are there which pass through this point, but do not intersect the line? Repeat with as many points and lines as you need to. Write a general statement which explains what you have discovered. 6. How ...
... 5. Remove one of these lines and keep the other. Now choose a point not on that line. How many lines are there which pass through this point, but do not intersect the line? Repeat with as many points and lines as you need to. Write a general statement which explains what you have discovered. 6. How ...
Four-dimensional space

In mathematics, four-dimensional space (""4D"") is a geometric space with four dimensions. It typically is more specifically four-dimensional Euclidean space, generalizing the rules of three-dimensional Euclidean space. It has been studied by mathematicians and philosophers for over two centuries, both for its own interest and for the insights it offered into mathematics and related fields.Algebraically, it is generated by applying the rules of vectors and coordinate geometry to a space with four dimensions. In particular a vector with four elements (a 4-tuple) can be used to represent a position in four-dimensional space. The space is a Euclidean space, so has a metric and norm, and so all directions are treated as the same: the additional dimension is indistinguishable from the other three.In modern physics, space and time are unified in a four-dimensional Minkowski continuum called spacetime, whose metric treats the time dimension differently from the three spatial dimensions (see below for the definition of the Minkowski metric/pairing). Spacetime is not a Euclidean space.