DOC
... Introduction Shape and space (also known as geometry) is the study of two- and three-dimensional objects and their properties. It involves understanding properties of angles, lines, reflection, rotation and enlargement. A particularly important aspect of Shape and space is the idea of proof. It is ...
... Introduction Shape and space (also known as geometry) is the study of two- and three-dimensional objects and their properties. It involves understanding properties of angles, lines, reflection, rotation and enlargement. A particularly important aspect of Shape and space is the idea of proof. It is ...
geometric congruence
... • AAS. (Also known as SAA.) If two triangles have 2 pairs of corresponding angles equal, as well as a pair of corresponding sides which is not in between them, the triangles are congruent. ∗ hGeometricCongruencei created: h2013-03-21i by: hCWooi version: h31467i Privacy setting: h1i hDefinitioni h51 ...
... • AAS. (Also known as SAA.) If two triangles have 2 pairs of corresponding angles equal, as well as a pair of corresponding sides which is not in between them, the triangles are congruent. ∗ hGeometricCongruencei created: h2013-03-21i by: hCWooi version: h31467i Privacy setting: h1i hDefinitioni h51 ...
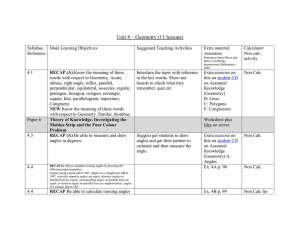
p. 1 Madison County Schools Suggested Geometry Pacing Guide
... Prove theorems about triangles. Theorems include: measures of interior angles of a triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a p ...
... Prove theorems about triangles. Theorems include: measures of interior angles of a triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a p ...
Symplectic Topology
... for R k = R l × R k−l (or simplify by φ 7→ f ). Theorem (Lie): If such a symmetry group is finite-dimensional and compact it’s SO(n), or SU (n) or SP (n) or one of a finite list of exceptions. [Drop compactness: get SO(p, q), SO(n, C ) etc, but still finitely many families.] Theorem (Cartan): If the ...
... for R k = R l × R k−l (or simplify by φ 7→ f ). Theorem (Lie): If such a symmetry group is finite-dimensional and compact it’s SO(n), or SU (n) or SP (n) or one of a finite list of exceptions. [Drop compactness: get SO(p, q), SO(n, C ) etc, but still finitely many families.] Theorem (Cartan): If the ...
Modern geometry 2012.8.27 - 9. 5 Introduction to Geometry Ancient
... The independence of the parallel postulate from Euclid's other axioms was finally proved by Beltrami in 1868. Erlanger Program In 1872, Klein tried to classify and characterize geometries on the basis of projective geometry and group theory. The problems of nineteenth century geometry Was there one ...
... The independence of the parallel postulate from Euclid's other axioms was finally proved by Beltrami in 1868. Erlanger Program In 1872, Klein tried to classify and characterize geometries on the basis of projective geometry and group theory. The problems of nineteenth century geometry Was there one ...
Geometry Notes 7-2 Ratios in Similar Polygons Recall, in congruent
... corresponding sides. Then write the similarity statement. Are all the pairs of angles congruent? m∠M = m∠T = 90 − 63 = 27°, so yes. ...
... corresponding sides. Then write the similarity statement. Are all the pairs of angles congruent? m∠M = m∠T = 90 − 63 = 27°, so yes. ...
15 the geometry of whales and ants non
... speed at depth, and then comes back up. In fact, we can be more precise about the nature of these curves: they are arcs of circles centered at the ocean surface! Thus, to a whale, what humans call a “circle” is actually a “line” (the shortest distance between two points). ...
... speed at depth, and then comes back up. In fact, we can be more precise about the nature of these curves: they are arcs of circles centered at the ocean surface! Thus, to a whale, what humans call a “circle” is actually a “line” (the shortest distance between two points). ...
Academic Geometry and Trigonometry Syllabus
... Coordinate Geometry Interpret and/or use linear, quadratic and/or exponential functions and their equations, graphs or tables Compute and/or use the slope of a line Apply appropriate techniques, tools and formulas to determine measurements Calculate midpoint of a segment Use all of the abo ...
... Coordinate Geometry Interpret and/or use linear, quadratic and/or exponential functions and their equations, graphs or tables Compute and/or use the slope of a line Apply appropriate techniques, tools and formulas to determine measurements Calculate midpoint of a segment Use all of the abo ...
Four-dimensional space

In mathematics, four-dimensional space (""4D"") is a geometric space with four dimensions. It typically is more specifically four-dimensional Euclidean space, generalizing the rules of three-dimensional Euclidean space. It has been studied by mathematicians and philosophers for over two centuries, both for its own interest and for the insights it offered into mathematics and related fields.Algebraically, it is generated by applying the rules of vectors and coordinate geometry to a space with four dimensions. In particular a vector with four elements (a 4-tuple) can be used to represent a position in four-dimensional space. The space is a Euclidean space, so has a metric and norm, and so all directions are treated as the same: the additional dimension is indistinguishable from the other three.In modern physics, space and time are unified in a four-dimensional Minkowski continuum called spacetime, whose metric treats the time dimension differently from the three spatial dimensions (see below for the definition of the Minkowski metric/pairing). Spacetime is not a Euclidean space.