PDF
... regarding defect for more details.) As an example, consider the disc {(x, y) ∈ R2 : x2 + y 2 < 1} in which a point is similar to the Euclidean point and a line is defined to be a chord (excluding its endpoints) of the (circular) boundary. This is the Beltrami-Klein model for H2 . It is relatively ea ...
... regarding defect for more details.) As an example, consider the disc {(x, y) ∈ R2 : x2 + y 2 < 1} in which a point is similar to the Euclidean point and a line is defined to be a chord (excluding its endpoints) of the (circular) boundary. This is the Beltrami-Klein model for H2 . It is relatively ea ...
GEOMETRY
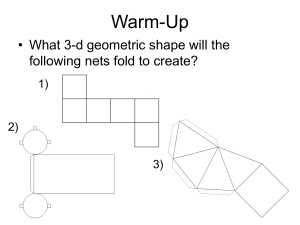
... “Net” is a two-dimensional layout of a threedimensional polyhedron Use a circle compass, a ruler, (compass), and paper to create a net for the following polyhedron. ...
... “Net” is a two-dimensional layout of a threedimensional polyhedron Use a circle compass, a ruler, (compass), and paper to create a net for the following polyhedron. ...
Geometry and Measures Year 5
... By the End of the year pupils are expected to reach or exceed Level 4c The following objectives should be taught in accordance with our Bishop King Maths Number policy. Children should begin their learning journey from the sub level that they are on and aspire to their age related expected end of ye ...
... By the End of the year pupils are expected to reach or exceed Level 4c The following objectives should be taught in accordance with our Bishop King Maths Number policy. Children should begin their learning journey from the sub level that they are on and aspire to their age related expected end of ye ...
temporal relationships for geo-spatial objects
... spatio-temporal geometry and topology models. Then, the taxonomy of spatio-temporal events between preceding and succeeding features was introduced. There are many other possibilities to describe spatio-temporal phenomena, for example, reincarnation could be a temporal continuous and spatio-temporal ...
... spatio-temporal geometry and topology models. Then, the taxonomy of spatio-temporal events between preceding and succeeding features was introduced. There are many other possibilities to describe spatio-temporal phenomena, for example, reincarnation could be a temporal continuous and spatio-temporal ...
SIMPLEST SINGULARITY IN NON-ALGEBRAIC
... (i.e. analytification of an algebraic scheme). A necessary condition for this to hold is that the transcendence degree of the field of global meromorphic functions must be equal to the dimension of the space, i.e. the space has to be Moishezon. For dimension 2, it is a classical result that it is al ...
... (i.e. analytification of an algebraic scheme). A necessary condition for this to hold is that the transcendence degree of the field of global meromorphic functions must be equal to the dimension of the space, i.e. the space has to be Moishezon. For dimension 2, it is a classical result that it is al ...
Use visualization, spatial reasoning, and geometric modeling to
... relationships among types of two and threedimensional objects using their definitions. • Understand relationships among the angles, side lengths, perimeters, areas, and volumes of similar objects; continued ...
... relationships among types of two and threedimensional objects using their definitions. • Understand relationships among the angles, side lengths, perimeters, areas, and volumes of similar objects; continued ...
8Mathstandards unit 4_1
... 2. Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them. 3. Describe the effect of dilations, ...
... 2. Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them. 3. Describe the effect of dilations, ...
1. What is meant by spacetime?
... a circle of radius r is 2πr. Open: Angles in a triangle add up to less than 180 degrees. Parallel lines diverge. The circumference of a circle of radius r is less than 2πr. Closed: Angles in a trainagle add up to more than 180 degrees. Parallel lines converge. The circumference of a circle of radius ...
... a circle of radius r is 2πr. Open: Angles in a triangle add up to less than 180 degrees. Parallel lines diverge. The circumference of a circle of radius r is less than 2πr. Closed: Angles in a trainagle add up to more than 180 degrees. Parallel lines converge. The circumference of a circle of radius ...
2nd 9 Weeks
... number from 1-10, count out that many objects. Decompose numbers less than or equal to 10 into pairs in more than one way, e.g. by using objects or drawings, and record each decomposition by a drawing or equation(e.g. 5=2+3 and 5=4+1) Compose and decompose numbers from 11 to 19 into ten ones and som ...
... number from 1-10, count out that many objects. Decompose numbers less than or equal to 10 into pairs in more than one way, e.g. by using objects or drawings, and record each decomposition by a drawing or equation(e.g. 5=2+3 and 5=4+1) Compose and decompose numbers from 11 to 19 into ten ones and som ...
Discovering Math: Exploring Geometry
... Congruent figures have exactly the same shape and size, and the ratio of their corresponding parts is 1:1. Similar figures have the same shape but different sizes, and their corresponding parts are proportional. Example 1: Proportion and Scale A model of the United States Capitol represents similar ...
... Congruent figures have exactly the same shape and size, and the ratio of their corresponding parts is 1:1. Similar figures have the same shape but different sizes, and their corresponding parts are proportional. Example 1: Proportion and Scale A model of the United States Capitol represents similar ...
READ - A Learning Place
... At the end of the lesson, children explain how they created their own problems. ...
... At the end of the lesson, children explain how they created their own problems. ...
Four-dimensional space

In mathematics, four-dimensional space (""4D"") is a geometric space with four dimensions. It typically is more specifically four-dimensional Euclidean space, generalizing the rules of three-dimensional Euclidean space. It has been studied by mathematicians and philosophers for over two centuries, both for its own interest and for the insights it offered into mathematics and related fields.Algebraically, it is generated by applying the rules of vectors and coordinate geometry to a space with four dimensions. In particular a vector with four elements (a 4-tuple) can be used to represent a position in four-dimensional space. The space is a Euclidean space, so has a metric and norm, and so all directions are treated as the same: the additional dimension is indistinguishable from the other three.In modern physics, space and time are unified in a four-dimensional Minkowski continuum called spacetime, whose metric treats the time dimension differently from the three spatial dimensions (see below for the definition of the Minkowski metric/pairing). Spacetime is not a Euclidean space.