Geometry 4th Nine Weeks Scope and
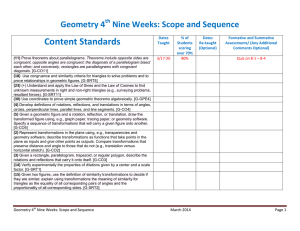
... (25) Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is perpendicular to the tangent where the radius intersects the c ...
... (25) Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is perpendicular to the tangent where the radius intersects the c ...
Lesson Plan Format
... 7-1 to 7-3 Quiz WEDNESDAY HW-pg. 465-466 (2-21) www.westex.org HS, Teacher Website Name _________________________ Geometry CPA 7-2 Ratio & Proportion Today’s Goal I will be able to: 1. identify similar polygons. 2. apply properties of similar polygons to solve problems. ...
... 7-1 to 7-3 Quiz WEDNESDAY HW-pg. 465-466 (2-21) www.westex.org HS, Teacher Website Name _________________________ Geometry CPA 7-2 Ratio & Proportion Today’s Goal I will be able to: 1. identify similar polygons. 2. apply properties of similar polygons to solve problems. ...
KUD Organizer
... Geometry is the investigation of the relationships and patterns that exist within shapes. Two-dimensional geometric figures are representations of our three-dimensional world. Experimenting with and investigating the relationships between two- and three-dimensional geometric figures connects and int ...
... Geometry is the investigation of the relationships and patterns that exist within shapes. Two-dimensional geometric figures are representations of our three-dimensional world. Experimenting with and investigating the relationships between two- and three-dimensional geometric figures connects and int ...
ppt
... Notes: 1. Traditional process algebras (Hoare, Milner) are based on the parallel operation of broadcast. The more basic operations are tensor and composition – broadcast is a derived operation, non-canonical since it depends on the choice of a monoid. (Span(Graph) should be used!) 2. A special case ...
... Notes: 1. Traditional process algebras (Hoare, Milner) are based on the parallel operation of broadcast. The more basic operations are tensor and composition – broadcast is a derived operation, non-canonical since it depends on the choice of a monoid. (Span(Graph) should be used!) 2. A special case ...
PDF
... The determinant above is positive if the three vectors satisfy the right-hand rule and negative otherwise. Recall that the magnitude of the cross product of two vectors is equivalent to the area of the parallelogram they form, and the dot product is equivalent to the product of the projection of one ...
... The determinant above is positive if the three vectors satisfy the right-hand rule and negative otherwise. Recall that the magnitude of the cross product of two vectors is equivalent to the area of the parallelogram they form, and the dot product is equivalent to the product of the projection of one ...
Geometry - Making Math Magic
... • Use the names of shapes to describe objects in the environment (K.G.A.1) • Describe the relative position of objects (for example, using terms such as above, below, beside, in front of, behind, next) (K.G.A.1) • Name the shapes regardless of orientation or size (K.G.A.2) • Identify shapes as two d ...
... • Use the names of shapes to describe objects in the environment (K.G.A.1) • Describe the relative position of objects (for example, using terms such as above, below, beside, in front of, behind, next) (K.G.A.1) • Name the shapes regardless of orientation or size (K.G.A.2) • Identify shapes as two d ...
Objectives Holt McDougal Geometry 11-1
... Classify three-dimensional figures according to their properties. ...
... Classify three-dimensional figures according to their properties. ...
Geometry - Shelton School District
... G.2.A Know, prove, and apply theorems about parallel and perpendicular lines. G.2.B Know, prove, and apply theorems about angles, including angles that arise from parallel lines intersected by a transversal. G.2.C Explain and perform basic compass and straightedge constructions related to parallel a ...
... G.2.A Know, prove, and apply theorems about parallel and perpendicular lines. G.2.B Know, prove, and apply theorems about angles, including angles that arise from parallel lines intersected by a transversal. G.2.C Explain and perform basic compass and straightedge constructions related to parallel a ...
6 Grade: 7 - simonbaruchcurriculum
... The study of Geometry was born in Ancient Greece, where mathematics was thought to be embedded in everything from music to art to the governing of the universe. Plato, an ancient philosopher and teacher, had the statement, “Let no man ignorant of geometry enter here,” placed at the entrance of his s ...
... The study of Geometry was born in Ancient Greece, where mathematics was thought to be embedded in everything from music to art to the governing of the universe. Plato, an ancient philosopher and teacher, had the statement, “Let no man ignorant of geometry enter here,” placed at the entrance of his s ...
1. The following figure is a box in which the top and bottom are
... 10. A student claims that if any two planes that do not intersect are parallel, then any two lines that do not intersect should also be parallel. How do you respond? No, it’s possible for two lines to be skew in three dimensions. In three dimensions, planes (2D objects) that do not intersect must be ...
... 10. A student claims that if any two planes that do not intersect are parallel, then any two lines that do not intersect should also be parallel. How do you respond? No, it’s possible for two lines to be skew in three dimensions. In three dimensions, planes (2D objects) that do not intersect must be ...
Four-dimensional space

In mathematics, four-dimensional space (""4D"") is a geometric space with four dimensions. It typically is more specifically four-dimensional Euclidean space, generalizing the rules of three-dimensional Euclidean space. It has been studied by mathematicians and philosophers for over two centuries, both for its own interest and for the insights it offered into mathematics and related fields.Algebraically, it is generated by applying the rules of vectors and coordinate geometry to a space with four dimensions. In particular a vector with four elements (a 4-tuple) can be used to represent a position in four-dimensional space. The space is a Euclidean space, so has a metric and norm, and so all directions are treated as the same: the additional dimension is indistinguishable from the other three.In modern physics, space and time are unified in a four-dimensional Minkowski continuum called spacetime, whose metric treats the time dimension differently from the three spatial dimensions (see below for the definition of the Minkowski metric/pairing). Spacetime is not a Euclidean space.























