Word
... This is exactly Kepler's Third Law with a = A. Note that the mass of the planet does not enter in to equation (1.22) so it applies for any planetary system in which the gravitational field is dominated by a single massive object. E: Gravitational fields from symmetrically distributed mass systems. N ...
... This is exactly Kepler's Third Law with a = A. Note that the mass of the planet does not enter in to equation (1.22) so it applies for any planetary system in which the gravitational field is dominated by a single massive object. E: Gravitational fields from symmetrically distributed mass systems. N ...
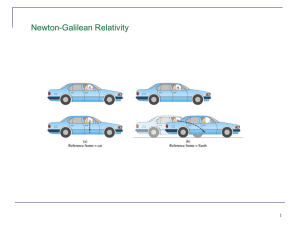
Lecture notes lecture 12 (relativity)
... The decay of a muon. A muon is a naturally occurring subatomic particle of nature that is unstable and transforms itself to other parts with a mean time to decay of 2.20μs (created by cosmic radiation high in Earth’s atmosphere). The muon(-/+) mass is roughly 310 times that of an electron (positron) ...
... The decay of a muon. A muon is a naturally occurring subatomic particle of nature that is unstable and transforms itself to other parts with a mean time to decay of 2.20μs (created by cosmic radiation high in Earth’s atmosphere). The muon(-/+) mass is roughly 310 times that of an electron (positron) ...
Introduction to group theory
... that there is a one-to-one correspondence between the elements of the two groups in a neighbourhood of any group element. This does not necessarily imply that there is a one-to-one correspondence between the two groups as a whole, i.e. the groups need not be globally equivalent. To understand the di ...
... that there is a one-to-one correspondence between the elements of the two groups in a neighbourhood of any group element. This does not necessarily imply that there is a one-to-one correspondence between the two groups as a whole, i.e. the groups need not be globally equivalent. To understand the di ...