Super Pressure Balloon Non-Linear Structural Analysis
... states is then presented. For this second case, the uni-axial modulus results are used for the initial region and the biaxial measurements are used for stress states higher than 15 MPa. B. Photogrammety Results and Strain Measurement The pressure at 249 Pa was used as the baseline for determining th ...
... states is then presented. For this second case, the uni-axial modulus results are used for the initial region and the biaxial measurements are used for stress states higher than 15 MPa. B. Photogrammety Results and Strain Measurement The pressure at 249 Pa was used as the baseline for determining th ...
Chap 8 Learn Obj
... 18. Determine whether or not a flaw of critical length is subject to detection given the resolution limit of the detection apparatus, the maximum applied tensile stress, the plane strain fracture toughness of the material, as well as a value for the scale parameter (Y). ...
... 18. Determine whether or not a flaw of critical length is subject to detection given the resolution limit of the detection apparatus, the maximum applied tensile stress, the plane strain fracture toughness of the material, as well as a value for the scale parameter (Y). ...
Liu.pdf
... density distributions of the stress and the strain, two models are presented for the reliability of the LCFL, and the randomness in the life characteristic of the material is taken into consideration in the presented models. The load-life interference and the equivalent probability transformation ar ...
... density distributions of the stress and the strain, two models are presented for the reliability of the LCFL, and the randomness in the life characteristic of the material is taken into consideration in the presented models. The load-life interference and the equivalent probability transformation ar ...
psaa forces worksheet
... will be deflected. Strain is the deformation of a material under the action of applied forces. A. A strain is a result of a stress. Stresses will produce strains proportionately until the proportional limit is reached. Ultimately, the strain will become so great, the material will fail. B. Structure ...
... will be deflected. Strain is the deformation of a material under the action of applied forces. A. A strain is a result of a stress. Stresses will produce strains proportionately until the proportional limit is reached. Ultimately, the strain will become so great, the material will fail. B. Structure ...
Connecting mesoscopic and macroscopic scale lengths for
... At least three length-scale levels are present to approach the micro-cracking phenomenon: macroscopic scale (~100µm), mesoscopic scale (~0.1µm to 10µm) and microscopic (atomistic) scale (~10-10 m). Until recently, the size scaling was neglected due to the early use of average stress (force per surfa ...
... At least three length-scale levels are present to approach the micro-cracking phenomenon: macroscopic scale (~100µm), mesoscopic scale (~0.1µm to 10µm) and microscopic (atomistic) scale (~10-10 m). Until recently, the size scaling was neglected due to the early use of average stress (force per surfa ...
An energy-based approach for estimates of the stress-strain
... The analysis of stress in notches, needed almost exclusively for fatigue design purposes, is performed with the help of the fatigue stress concentration factor kf . Again the material behavior is assumed to be linear elastic and the little plasticity, if present, is believed to be confined at a pret ...
... The analysis of stress in notches, needed almost exclusively for fatigue design purposes, is performed with the help of the fatigue stress concentration factor kf . Again the material behavior is assumed to be linear elastic and the little plasticity, if present, is believed to be confined at a pret ...
CHAPTER 12 STATIC EQUILIBRIUM AND ELASTICITY • Conditions
... If the origin is taken at the center of gravity, then the object produces zero torque about that point. The center of gravity is then ... the point about which the gravitational force on the object produces zero torque no matter what the orientation of the object. It could also be called ... the cen ...
... If the origin is taken at the center of gravity, then the object produces zero torque about that point. The center of gravity is then ... the point about which the gravitational force on the object produces zero torque no matter what the orientation of the object. It could also be called ... the cen ...
on plastic void growth in strong ductile materials
... The plots in Fig. 3 reveal a relatively mild effect of elastic compressibility on the value of σcr . For the considered material properties, an increase of Poisson’s ratio from 1/3 to 1/2 increases the critical stress by about 5%. The value of the yield stress Y was selected to facilitate the compar ...
... The plots in Fig. 3 reveal a relatively mild effect of elastic compressibility on the value of σcr . For the considered material properties, an increase of Poisson’s ratio from 1/3 to 1/2 increases the critical stress by about 5%. The value of the yield stress Y was selected to facilitate the compar ...
11510079-c-A-6.pdf
... electric-field-induced deformation. However, the term is most often used to refer to an electric-field-induced deformation that is proportional to the square of the electric field, as illustrated in Fig. 6.1b, εij = Mijkl E k El . ...
... electric-field-induced deformation. However, the term is most often used to refer to an electric-field-induced deformation that is proportional to the square of the electric field, as illustrated in Fig. 6.1b, εij = Mijkl E k El . ...
p250c09
... Example: A cylindrical winch of radius R and moment of inertia I is free to rotate without friction. A cord of negligible mass is wrapped about the shaft and attached to a bucket of mass m. What is the acceleration of the bucket when it is released? ...
... Example: A cylindrical winch of radius R and moment of inertia I is free to rotate without friction. A cord of negligible mass is wrapped about the shaft and attached to a bucket of mass m. What is the acceleration of the bucket when it is released? ...
Dislocation density evolution upon plastic deformation of Al-Pd
... dislocation density decrease « ˆ 5:7 109 cm 2 between the values at 5.2 and 11.1% plastic strain, a di erence in internal stress of 11.7 MPa follows. For this calculation we have used the same values for ¬ , b and · as for the calculation of the yield drop. The observed decrease ¼ in the ¯ ow stres ...
... dislocation density decrease « ˆ 5:7 109 cm 2 between the values at 5.2 and 11.1% plastic strain, a di erence in internal stress of 11.7 MPa follows. For this calculation we have used the same values for ¬ , b and · as for the calculation of the yield drop. The observed decrease ¼ in the ¯ ow stres ...
Smart materials for active noise and vibration reduction
... piezoelectric effect causes a solid to become strained when placed in an electric field. Thus, piezoelectric ceramics can both be used as sensor and actuator. Piezoelectric ceramics are polycrystalline in nature and do not have piezoelectric characteristics in their original state. Piezoelectric eff ...
... piezoelectric effect causes a solid to become strained when placed in an electric field. Thus, piezoelectric ceramics can both be used as sensor and actuator. Piezoelectric ceramics are polycrystalline in nature and do not have piezoelectric characteristics in their original state. Piezoelectric eff ...
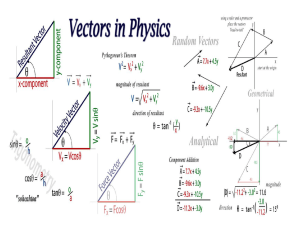
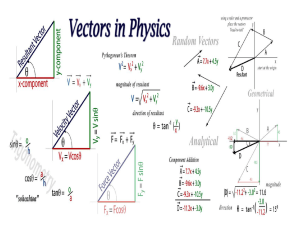
Chapter 3 Two-Dimensional Motion and Vectors
... Adding Vectors that are not Perpendicular Suppose that a plane travels first 5 km at an angle of 35°, then climbs at 10° for 22 m, as shown below (you must draw). How can you find the total displacement? Because the original displacement vectors do not form a ________________ triangle, you can n ...
... Adding Vectors that are not Perpendicular Suppose that a plane travels first 5 km at an angle of 35°, then climbs at 10° for 22 m, as shown below (you must draw). How can you find the total displacement? Because the original displacement vectors do not form a ________________ triangle, you can n ...
Constitutive Laws
... provided state variables do not undergo an appreciable fractional change in: A spatial region of the dimension ca. one ...
... provided state variables do not undergo an appreciable fractional change in: A spatial region of the dimension ca. one ...
lithospheric strength profiles
... hydrostatic pressure) tend to change the volume of the material and are resisted by the body's bulk modulus, which depends on the Young's modulus and Poisson ratio. Shear stresses tend to deform the material without changing its volume, and are resisted by the body's shear modulus. Strain energy In ...
... hydrostatic pressure) tend to change the volume of the material and are resisted by the body's bulk modulus, which depends on the Young's modulus and Poisson ratio. Shear stresses tend to deform the material without changing its volume, and are resisted by the body's shear modulus. Strain energy In ...
Chapter 12
... constant angular velocity relative to an observer in an inertial reference frame. Will deal now with the special case in which both of these velocities are equal to zero This is called static equilibrium. Static equilibrium is a common situation in engineering. The principles involved are of parti ...
... constant angular velocity relative to an observer in an inertial reference frame. Will deal now with the special case in which both of these velocities are equal to zero This is called static equilibrium. Static equilibrium is a common situation in engineering. The principles involved are of parti ...
12.3 - De Anza
... constant angular velocity relative to an observer in an inertial reference frame. Will deal now with the special case in which both of these velocities are equal to zero § This is called static equilibrium. Static equilibrium is a common situation in engineering. The principles involved are of parti ...
... constant angular velocity relative to an observer in an inertial reference frame. Will deal now with the special case in which both of these velocities are equal to zero § This is called static equilibrium. Static equilibrium is a common situation in engineering. The principles involved are of parti ...
Chapter 5 - Stress in Fluids
... The only material property of the fluid we have so far discussed is the density. In the last chapter we introduced the rate of deformation or rate of strain tensor. The distinguishing characteristic between fluids and solids is that fluids can undergo unlimited deformation and yet maintain its integ ...
... The only material property of the fluid we have so far discussed is the density. In the last chapter we introduced the rate of deformation or rate of strain tensor. The distinguishing characteristic between fluids and solids is that fluids can undergo unlimited deformation and yet maintain its integ ...
uncorrected page proofs
... rubber bands when under load. How much an object deforms depends on the magnitude of the applied force and the physical properties of the material it is made from. The bones, muscles and tendons in our bodies also respond to forces by deforming. A change in length of our muscles and tendons is more ...
... rubber bands when under load. How much an object deforms depends on the magnitude of the applied force and the physical properties of the material it is made from. The bones, muscles and tendons in our bodies also respond to forces by deforming. A change in length of our muscles and tendons is more ...
Introduction to Continuum Mechanics
... since dX is infinitesimal the higher order term o(2) tends to zero. Similarly, let daκ and nκ be a small material surface element and its unit normal in the reference configuration and da and n be the corresponding ones in the deformed configuration. And let dvκ and dv be small material volume eleme ...
... since dX is infinitesimal the higher order term o(2) tends to zero. Similarly, let daκ and nκ be a small material surface element and its unit normal in the reference configuration and da and n be the corresponding ones in the deformed configuration. And let dvκ and dv be small material volume eleme ...
Deformation (mechanics)
Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body.A deformation may be caused by external loads, body forces (such as gravity or electromagnetic forces), or changes in temperature, moisture content, or chemical reactions, etc.Strain is a description of deformation in terms of relative displacement of particles in the body that excludes rigid-body motions. Different equivalent choices may be made for the expression of a strain field depending on whether it is defined with respect to the initial or the final configuration of the body and on whether the metric tensor or its dual is considered.In a continuous body, a deformation field results from a stress field induced by applied forces or is due to changes in the temperature field inside the body. The relation between stresses and induced strains is expressed by constitutive equations, e.g., Hooke's law for linear elastic materials. Deformations which are recovered after the stress field has been removed are called elastic deformations. In this case, the continuum completely recovers its original configuration. On the other hand, irreversible deformations remain even after stresses have been removed. One type of irreversible deformation is plastic deformation, which occurs in material bodies after stresses have attained a certain threshold value known as the elastic limit or yield stress, and are the result of slip, or dislocation mechanisms at the atomic level. Another type of irreversible deformation is viscous deformation, which is the irreversible part of viscoelastic deformation.In the case of elastic deformations, the response function linking strain to the deforming stress is the compliance tensor of the material.