Download uncorrected page proofs

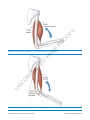
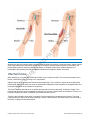
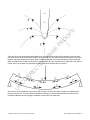
CHAPTER 16 How do forces act on the human body?
Contents
O
PR
O
G
E
PA
TE
D
R
EC
Equilibrium — staying in place
Centre of mass
Centre of gravity
Working out
Internal forces
Under stress and strain
Stress
Strain
Which one is stronger?
Stiffness
Young’s modulus of elasticity
Materials for a purpose
Strain energy
Toughness
Elastic behaviour
Plastic behaviour
Choosing materials to perform
Materials for protheses
Common construction materials
When the going gets hot
Tired out
Given enough time
Metals
Metal in prosthetic limbs
FS
Forces in the human body
R
Chapter review
N
C
Questions
O
Summary
U
Note to students and teachers: This PDF has been provided as an offline solution for times when you do not have
internet access or are experiencing connectivity issues. It is not intended to replace your eBook and its suite of
resources. While we have tried our best to replicate the online experience offline, this document may not meet
Jacaranda's high standards for published material. Please always refer to your eBook for the full and latest
version of this title.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
R
EC
TE
D
PA
G
E
PR
O
O
FS
CHAPTER 16 How do forces act on the human body?
N
C
REMEMBER
O
R
Try to think of your body as a structure made of bone, tendons, muscles and skin. To find out what the body is
capable of, we will look at the forces and loads on these structures.
U
Before beginning this chapter you should be able to:
■
describe mechanical levers
■
recall the structure of the skeletal and musculature systems of the human body.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
KEY IDEAS
After completing this chapter you should be able to:
identify different types of forces that act on the human body
■
calculate the centre of mass of a system
■
model translational forces and torque
■
calculate stress and strain
■
apply Young’s modulus
■
compare building materials with human tissues
■
use stress and strain graphs to calculate the potential energy stored in a material
■
investigate the materials used in prosthetics, both internal and external
■
compare the functions and longevity of natural and artificial limbs.
PR
O
G
E
Forces in the human body
O
FS
■
PA
We work, we play, we move. Lift an object and you feel it pull on your arm. Throw or catch a ball and you feel it
push on your hand. You should also feel something happening inside your body. Perhaps you’ll feel a particular
muscle when pushing off to run or when jumping to catch a ball.
EC
TE
D
Forces generated by our muscles enable our bones to move relative to each other; that’s how we move. This
happens when we bend, run or sit, whether we are exercising vigorously, sitting down or turning around to look
over our shoulder. Even when we are standing still our muscles work to help us keep our balance. Humans must
be strong enough to create these internal forces and safely respond to the external forces that act on us.
Equilibrium — staying in place
R
The net external force acting on a stationary object must be zero because its acceleration is zero.
U
N
C
O
R
Whether we are stationary or moving the primary external force we experience is caused by gravity. For us to
stand still, the gravitational force acting on us, mg, must be balanced by the force from the ground, which is equal
in magnitude and opposite in direction to our weight.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
U
N
C
O
R
R
EC
TE
D
When suspended from the horizontal bar shown in the figure below, the person is balanced. The force, T, in each
of the arms can be calculated using the principles of equilibrium.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
F  0
2T cos30  mg  0
mg
2 cos30
T  0.58mg
T 
Rotational equilibrium
If an object is in equilibrium, the torque caused by one force must be balanced by the turning effect of one or
more other forces.
R
EC
TE
D
PA
G
E
PR
O
O
FS
The effect of torque can be seen if you stand with your heels touching a wall. Keeping your legs straight and
without moving your feet, try to bend forwards to touch your toes or ankles. You should lose your balance and fall
forwards.
R
Now stand clear of the wall and any furniture or other objects. While keeping your legs straight, bend forwards to
try and touch your ankles. This time you should be able to keep your balance.
N
C
O
When you stood against the wall, two forces were acting on you: your weight, mg, and the reaction from the floor,
R. Although translational equilibrium was satisfied, that is R + mg = 0, with your straight legs and heels touching
the wall, the force, mg, could not act along the same line as R. Rotational equilibrium was not satisfied and the
pair of forces caused a rotation, meaning you lost your balance.
U
In contrast, when you were not restrained by the wall, you could adjust your body position so that your centre of
gravity was over your feet. You were able to keep your balance when your weight and the reaction from the floor
acted along the same vertical line. Under these conditions, rotational equilibrium was satisfied.
Centre of mass
When applying Newton’s laws, it is often convenient to consider the mass of an object to be concentrated at a
single point, and that the net force acting on the object acts through that single point. We refer to that
concentration of mass as the centre of mass (CM). The centre of mass of a symmetrical object with uniformly
distributed mass is at the centre of the object. For example, the centre of mass of an orange is at its centre. If the
object is symmetrical in two dimensions, the CM will be at the intersection of the two lines of symmetry, as shown
below.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
A symmetrical object behaves as if its mass were concentrated in the middle, where its lines of symmetry
intersect
PA
If you support an object under its centre of mass, it will balance. Applying a force through the CM of an object will
not cause rotation.
TE
D
AS A MATTER OF FACT
When an object is hung from a single point, the CM will be on the same vertical line as the support. The CM of an
object like a table tennis bat can be found by hanging it successively from more than one position and using the
gravitational field and a plumb bob as shown in the figure below. The CM is where the lines intersect.
U
N
C
O
R
R
EC
Try using this method to find the CM of Victoria or Australia. Where is the CM of a doughnut? Where is it on a
banana or a boomerang?
Using a plumb bob to find the centre of mass of a table tennis bat
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
PR
O
O
FS
However, the centre of mass for some objects, such as a banana or a doughnut, are not within the object.
U
N
C
O
R
R
EC
TE
D
PA
G
E
The position for the CM can be determined mathematically by using the equation for rotational equilibrium.
Rotational equilibrium has been used to locate the CM of the tray and contents being carried by the waiter in the
figure below.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
TE
D
EC
R
R
O
C
N
U
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
F  0
4N  2N  2N R  0
R  8 N upwards
  0, take torques about the CM of the tray
2 N 0.2 m  R  d  4 N  (0.2  d )  0; and substituting for R
12  d  0.4 m
d  0.033 m  3.3cm
To balance the tray, the waiter should place his hand 3.3 cm from the centre of the tray.
x 1 m1  x 2 m2   x i mi
(where i is the number of objects)
m1  m2   mi
O
x CM 
FS
The location of the centre of mass of a system of two or more objects can be found using the formula:
PR
O
Centre of gravity
For most objects on or near the Earth’s surface, it is reasonable to assume that the centre of gravity is at the
same point as the centre of mass.
G
E
Even though each part of our body — torso, head, arms and legs — contributes its own weight to our total weight,
it is usually convenient to consider the total weight of a person as acting through a single point, our centre of
gravity (CG).
U
N
C
O
R
R
EC
TE
D
PA
When looked at from the front, a standing person is symmetrical about the vertical line passing through the middle
of their body, and their CM is at approximately waist level. Looked at from the side, a standing person is not
symmetrical, but their CM is still approximately at waist level and in the middle of their body.
When we move a limb or bend, we change our body shape and there is a corresponding change in our centre of
mass. Moving a limb moves our CM in the same direction. When we tuck during a dive, curl up to pole vault, or
arch our backs during a high jump we change the location of our centre of mass. Bend far enough and our CM will
move to a point outside our body. This enables us to move in different ways.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
Bending into a tuck, the diver performing a somersault relocates their CM to outside their body. The change in
position of the CM enables the diver to rotate about their centre of mass. Before entering the water the diver
straightens their body and stops the somersault.
PA
Working out
TE
D
Systems of muscles, bones and tendons in our body work together to enable us to move. They also work to keep
us balanced when we are stationary.
EC
When Jo is standing and stationary, two forces are acting on him: his weight, mg, and the reaction from the
ground, R. The force in each leg is equal to half his weight, mg2 , and acts downwards. However, what happens
when Jo stands on his toes? The external forces, his weight and the reaction from the ground have not changed,
but he can feel his calf muscles stretch and he will eventually tire.
U
N
C
O
R
R
Let’s look at the forces in Jo’s feet in isolation from the rest of his body. Using a diagram to consider the
equilibrium of his feet, all of the forces acting on his feet need to be shown, whether the forces are known or
unknown. While it might not be initially clear whether an unknown force is pushing or pulling, this will become
apparent after the calculations have been completed.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
TE
D
EC
R
R
There is a force caused by the rest of Jo’s body pushing down on his ankles, primarily through his talus, the bone
in his ankle at the base of his leg. This force is shown in the figure as force B. Jo’s calf muscles are pulling
upwards through the Achilles tendon at the back of his ankle, shown as force T, acting upwards. There is also the
reaction from the ground, R, which also acts upwards.
C
O
Considered as isolated objects, Jo’s feet are in equilibrium, so the net force acting on his feet must be zero.
mg
2
.
N
For translational equilibrium to be satisfied B – T – R = 0. We know that on each foot R 
U
Taking torques about the line of effort of one of the unknown forces, in this case T, and assigning clockwise
torque as positive and anti-clockwise torques as negative, we find:
0.030 T 
T 
0.120 mg
0
2
0.120 mg
0.060
T  2.00 mg in each leg.
By substitution, the force in the talus (T) can be calculated.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
B T R
B  2.00 mg 
mg
2
B  2.50 mg in each leg.
Jo’s feet act as levers with their fulcrum at the ball of his feet. To stand on his toes, Jo creates a force in his
muscles, and his tendons pull upwards at the back of his ankles. This in turn increases the magnitude of the force
in the bones in Jo’s legs.
FS
In this example, the force needed to lift Jo’s legs is less than the force in the bones of the leg. The levers, his feet,
are said to have provided a mechanical advantage, which is fundamental to our walking and being able to quickly
accelerate when running.
PR
O
O
There are many other muscle, tendon and bone systems in our bodies forming levers that might be necessary to
stabilise us, enable us to move — sometimes quickly or through relatively large distances — or to perform fine
movements as might be required by a neurosurgeon. Of the three types of levers shown in the figure below,
examples of each can be found in the human body.
U
N
C
O
R
R
EC
TE
D
PA
G
E
In a first-class lever, the load and force are either side of the fulcrum. In a second-class lever, the load is between
the fulcrum and the force and in a third-class lever, the force is between the fulcrum and the load.
(a) A first-class lever, (b) a second-class lever, (c) a third-class lever
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
U
N
C
O
R
R
EC
TE
D
PA
When you bend your arm to lift a load, your forearm acts as a third-class lever.
When you straighten your arm to push downwards, your forearm acts as a First-class lever.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
PA
G
E
PR
O
O
FS
When we nod up and down, our head rotates about the top of our spine. This is an example of a first-class lever
in which our skull is the lever. The centre of mass of our head is forward of our spine and the muscles at the back
of our neck provide the force to counter the head’s weight, rotating about the top of the spine. This lever
mechanism is important as it stabilises our head and neck.
U
N
C
O
R
R
EC
TE
D
Splinting is another example of a first-class lever that is used to support parts of our body. The wrist splint in the
figure below might be used to protect a wrist following a fracture or sprain, while also enabling functional use of
the hand. With the fulcrum at the heel of the palm of the hand, a force acting up on the hand, U, is resisted by the
force R at the end of the splint to the right.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
Jo standing on his toes was an example of a second-class lever in which the force he created was able to lift a
larger force, therefore providing him with a mechanical advantage.
EC
TE
D
PA
G
E
PR
O
O
FS
Third-class levers are more common in our body. If you lie face down you then flex your knee to raise your foot,
your lower leg, knee joint and hamstring act as a third-class lever. In such cases, the muscle is not necessarily
pulling at right angles to the bone. The efficiency of the force generated by the muscles depends on the angle of
its insertion to the bone. The efficiency also changes as you flex your knee because the perpendicular distance
from your knee to the centre of gravity of your lower leg decreases.
O
R
R
Although the force needed by your hamstrings is large compared to the weight of your lower leg, this type of lever
enables fast and extensive movement of your leg. Contracting your muscles a small amount will cause a larger
movement in your leg.
U
N
C
While the fundamental principles of levers can be applied to a system, identifying which muscles are acting can
be complex, particularly as an apparently simple action might involve more than one muscle, or group of muscles,
at different stages of the movement. For example, when using your forearm to lift a cup you might engage two
different muscle groups, the brachialis (biceps) and the brachioradialis. Using your brachialis muscles is an
example of a third-class lever with your elbow the fulcrum. However, when engaging the brachioradialis you
create a second-class lever.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
TE
D
Lifting your arm using the brachialis or bicep(left) and brachioradialis (right)
R
R
Internal forces
EC
Whereas one group of muscles might provide the force necessary to produce or resist movement, another muscle
group might control the movement by opposing it. For example, while the biceps might act to lift an object, the
triceps might control the action by resisting the biceps. An analysis of these lever systems depends on a
knowledge of both anatomy and the principles of mechanics as it applies to human movement.
O
When standing on your toes, the tendons at the back of your ankles are pulled. The muscles and tendons are in
tension, whereas the bones in the leg are in compression.
U
N
C
Objects respond to compressive and tensile forces by deforming. This is evident in objects such as springs and
rubber bands when under load. How much an object deforms depends on the magnitude of the applied force and
the physical properties of the material it is made from.
The bones, muscles and tendons in our bodies also respond to forces by deforming. A change in length of our
muscles and tendons is more noticeable than changes in our bones, except when a bone fractures. However, our
bones do compress and bend in response to the forces that act on them.
Tension is also created in the walls of our arteries from the blood being circulated around our body. The blood
travelling along our arteries is like water travelling in a hose. Under pressure, the blood pushes out on the wall of
the artery, causing circumferential tension.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
TE
D
EC
R
U
N
C
O
R
The skin is the largest organ in the human body. Push on your skin and it will depress and stretch. When you
pushed on your skin you caused a multidirectional tensile force in it. This is a special example of tension in that
the primary deformation is transverse to the force you applied. This might be likened to a tight rope stretching
when walked on, the difference being that the skin is a membrane and the resulting tension will occur in several
directions.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
U
N
C
O
R
R
EC
TE
D
There are forces that cause deformations different to those caused by tensile and compressive forces. Bending
and shear are two such forces. When bending, an object tends to curve. Some sections of the object move closer
together and other sections move further apart, causing compression on one side and tension on the other side.
When you stand in the middle of a plank that is supported at both ends, it bends and you might feel it sag. When it
is bent, the top of the plank is compressed and the underside is stretched and is in tension.
Shear forces create a tendency for part of an object to slide over itself; the effect is similar to a sideways force
acting on a thick book. The top of the book displaces sideways, the bottom remains stationary, and there is a
proportional displacement of the pages in between as they slide over each other.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
U
N
C
O
R
R
EC
TE
D
PA
G
E
PR
O
O
FS
When a person grinds their teeth, they create shear forces that erode the surface of the tooth and sometimes
cause the tooth to fracture. The tennis player in figure below is also creating shear forces in their foot when they
slide, or try to push on the court, risking injury to their ankle.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
Under stress and strain
To survive a bungee jump, people rely on the suitable choice of bungee cord. The cord must stop the free fall
before the jumper hits the ground, and must cushion the fall by absorbing the deceleration. An unsuitable choice
of a cord could be fatal. If the bungee jumper is heavier, instinct and experience would suggest that a thicker cord
should be used. The thicker cord will be stronger and have a greater resistance to deformation. If a person is
jumping from a greater height, then a longer cord will be needed, but the longer cord will also stretch further.
FS
Similarly, it is important that our muscles and tendons do not break, or stretch too much, when resisting external
forces. They also need to tolerate the internal forces necessary for balance and movement. There are many
factors that make some materials strong or flexible, and the physical quantities stress and strain are helpful in
classifying and predicting the behaviour of materials, including those in our body. To compare meaningfully the
performance of different sized forces on different sized objects, we measure stress and strain.
O
Stress
U
N
C
O
R
R
EC
TE
D
PA
G
E
PR
O
We use stress to compare the strength of materials — a strong material will sustain a larger stress than a weak
force F
material. Stress is defined as the force per unit area of cross-section supporting a force.   stress 
= .
area A
−2
Stress is measured in pascals, where 1 Pa = 1 N m . However, for many materials such as those used in the
construction of buildings, it is more convenient to use megapascals, MPa, where 1 MPa = 1 × 106 Pa.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
SAMPLE PROBLEM 16.1
TE
D
PA
G
E
PR
O
O
FS
The femur in the figure below must support 340 N.
EC
Assuming that the femur is homogenous and at mid-length is cylindrical with a diameter of 26 mm, what is the
stress in the bone?



R
O

C

340 N
  132 mm 2
530 mm 2
5.3  10 4 m 2
F
A
340 N
5.3  10 4 m 2
6.4  105 Pa
0.64 MPa
N




U
F
A
R
Solution:
At its mid-length, the femur is almost cylindrical. However, to aid our joints in sustaining compressive and impact
forces, the femur flares out to form the condyles, just above the knee. The femur also becomes larger at its head,
just below the hip. The magnitude of the force in the bone does not change, but the change in shape of the femur
towards its ends increases the cross-sectional area, so there is a corresponding decrease in the stress at the
joints. The smaller stress reduces wear and tear in the joint and helps with cushioning against impact.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
Strain
When a stress is applied to a material, it changes shape. Strain is a measure of the magnitude of this
deformation. The amount a material deforms depends on its initial length in the direction of the force. For
example, when pulling on a short piece of fishing line, you could not stretch it as far as when applying the same
force to a longer piece of the same fishing line. Similarly, when under the same stress, the change in length of a
tendon would be different from that for a longer piece of the same tendon. For this reason, we use strain to
compare the fractional change in length of materials.
Strain, ε, is the ratio of the change in length to the original length.
l
L
FS

where
PR
O
O
∆l = the change in length measured in metres
L = the original length measured in metres.
Note: Strain does not have any units; it is dimensionless!
G
E
In many materials strain is so small that it is hardly noticeable, but it is always there in response to stress.
PA
The strain of a material when it breaks is often expressed as a percentage and called the percentage elongation.
SAMPLE PROBLEM 16.2
TE
D
Camille’s Achilles tendon is 200 mm long. When Camille stretches her tendon to 208 mm, what is the strain?
Solution:
l
L
(208  200)

200
 0.04 or 4%
U
N
C
O
R
R
EC
 
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
SAMPLE PROBLEM 16.3
Camille then ruptured her Achilles tendon when the strain reached 10%. How much had the tendon stretched
when it ruptured?
Solution:
FS
l
l
L
 L
 0.10  200 mm
 20 mm

O

PR
O
Which one is stronger?
There is no such thing as an absolutely rigid material. Every solid material will deform, even though the
deformation is often so small that it is not visible. Excessive or permanent deformation could make an object
unserviceable. Fortunately, many objects recover their original shape when the force is removed.
G
E
Stiffness
PA
When a force deforms a material, it does work against internal forces. Whether it is a bone being compressed or a
tendon stretching, work is done by moving tissues and cells either closer together or further apart. If the material
is stiffer, the amount of work required to deform it will be greater. Knowing the stiffness of materials enables us to
predict their behaviour when acted on by a force.
EC
TE
D
Stress and strain are used to compare the properties of materials because they are independent of the size and
shape of the material. Scientists and engineers gather this information by conducting laboratory tests on small
samples of materials. Information from these tests enables engineers to choose the most appropriate material,
and the required amount of material, for a particular use.
U
N
C
O
R
R
Tension tests are typically carried out on small bars that are stretched until the specimen breaks. Compression
tests are performed by crushing blocks or cylinders. The stress applied and the subsequent deformation of a
material may be displayed as a stress– strain graph. The strength of a material is the largest stress applied before
it fails and is often available from the stress–strain graph.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
TE
D
EC
R
R
A tensile testing apparatus
U
N
C
O
Tensile tests carried out on construction materials such as metals are usually undertaken using apparatus similar
to that shown in the image above. These tests assume that the composition and behaviour of the material being
tested is the same throughout; that is, it is homogenous. It is also assumed that the material is isotropic — its
properties are the same in each direction. While the assumptions of homogeneity and isotropy might not apply to
biological materials, such as skin, the tensile tests can still be used to inform us of their mechanical properties.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
σ–ε relationship for a skin sample
TE
D
The mechanical properties of skin vary according to many factors, including where on the body the skin comes
from, its age, level of hydration and how quickly the force is applied to the test sample.
U
N
C
O
R
R
EC
In the case of living tissue such as that found in the human body, medical scientists might obtain stress and strain
information by testing in vivo — alive and on the body — or in vitro — after removing the material from the body.
An understanding of the behaviour of different materials, including those occurring naturally in the human body,
has helped develop artificial devices to help people with implants, prostheses and orthoses.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
SAMPLE PROBLEM 16.3
O
R
R
EC
TE
D
PA
G
E
PR
O
O
FS
Which of the two materials in the graph below is stronger? Which elongates the most before breaking?
C
Solution:
U
N
Material 1 is stronger because a greater stress was needed to break it. However, material 2 stretched more
before breaking.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
SAMPLE PROBLEM 16.4
EC
TE
D
PA
G
E
PR
O
O
FS
Consider the two materials represented in the stress–strain graph shown in the figure below. Of the two materials,
which would be more difficult to stretch?
R
Solution:
R
A stiff material requires a larger stress in order to strain it the same amount as a less stiff material.
N
C
O
The stress needed to produce a strain, ε, in material 1 is larger than the stress needed to produce the same strain
in material 2. Material 1 is harder to stretch and is said to have a greater stiffness. Note the steeper gradient of
the stress–strain curve for the stiffer material.
U
The shape of the stress–strain graph for different materials varies as shown in the following figure.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
Young’s modulus of elasticity
PA
G
E
For many materials, the stress–strain graph for a tensile test is straight, or nearly straight, near the origin. Here,
the stress in the material is proportional to the strain and the constant of proportionality is called the modulus of
elasticity or Young’s modulus’, E.
Young’s modulus is calculated from the gradient of the stress–strain curve, E 

. This relationship is an

U
N
C
O
R
R
EC
TE
D
expression of Hooke’s Law and can be written in the form σ = E × ε.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
TE
D
EC
R
R
O
U
N
C
A material with a higher Young’s modulus is stiffer; it is more resistant to deformation as shown by the steeper
gradient of the stress–strain curve. Steel is used in large and small structures because it is stiff and needs a large
stress to change its shape. Materials that have a low Young’s modulus would not be suitable for buildings
because they would deform too much. The modulus for most materials is large, so it is usually expressed in
gigapascals, where 1 GPa = 109 Pa.
For the material represented graphically above:
E





180 MPa

3  10 3
 6  10 4 MPa

Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
So, for this material E = 60 GPa. Some typical values of E are listed in table 16.1.
TABLE 16.1 Some typical values of E
Material
Young’s modulus (GPa)
7
Bone
7–30
Wood
14
Concrete
18
Aluminium
70
Glass
100
Titanium
100
Copper
110
Steel
210
Carbon fibre
410
Diamond
1200
O
Polyethylene
PR
O
2
G
E
Tendon
FS
2 × 10–4
Skin
U
N
C
O
R
R
EC
TE
D
PA
Our bones are not homogenous. They comprise a hard outer layer called cortical bone, and a spongy interior
named trabecular bone. Before it breaks, the bone exhibits a linear stress–strain relationship. When considered
as a whole, the stress–strain graph of a bone sample is as shown in the figure below.
The stress–strain graph is linear and Young’s modulus can be calculated from the graph.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
E


120 MPa

0.009
 1.3  10 4 MPa

So, for this sample of bone E = 13 GPa.
R
EC
TE
D
PA
G
E
PR
O
O
FS
Even in materials that do not exhibit a linear stress–strain relationship, the slope of the curve is often used to
describe the stiffness of the material. For the skin sample shown below, the slope of the linear part of the graph
provides an estimate of Young’s modulus — a measure of the stiffness of the skin within its elastic range.
O
R
Stress–strain graph of a skin sample
N


0.02 MPa

(0.80  0.70)
 0.2 MPa

U
E
C
From the graph, Young’s modulus can be calculated. For example, when subject to larger stress:
So, for this sample of skin E = 0.2 MPa = 200 kPa
Note that the skin initially deforms without carrying much stress. After it deforms, it behaves more stiffly. When
under stress the skin will deform, something which is important if the body is to accommodate movement at joints.
The ability of the skin to stiffen and resist larger stresses then protects other parts of the body, such as vital
organs, from penetration.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
SAMPLE PROBLEM 16.5
Using the test data shown in table 16.2, plot a stress–strain curve and calculate Young’s modulus for each
material. Which material is stiffer? Which is stronger?
0
0
35
0.5
70
1.0
110
1.5
140
2.0
145
2.3
150
2.5
0
0
30
0.5
60
1.0
90
1.5
110
2.0
130
3.0
140
4.0
O
Material A
Stress (MPa)
Strain (× 10–3)
Material B
Stress (MPa)
Strain (× 10–3)
FS
TABLE 16.2 Test data for two materials (A and B)
Using the straight region of the graphs to calculate Young’s modulus:
Material A
 stress
 strain
G
E
E =
140
MPa
2.0× 10 3
= 7× 10 4 MPa
PA
=
= 70 G Pa
TE
D
Material B
E =
PR
O
Solution:
 stress
 strain
90
MPa
1.5× 10 3
= 6× 10 4 MPa
EC
=
R
= 60 G Pa
O
R
From the graph shown, it can be seen that the slope of the curve for A is steeper than that for B; therefore, A is
stiffer than B.
U
N
C
The maximum stress that material A can sustain before fracture is greater than that for material B: 150 MPa
compared with 140 MPa. Therefore, material A is stronger than material B.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
REVISION QUESTION 16.1
N
C
O
R
R
EC
TE
D
PA
G
E
PR
O
O
FS
What is the value of Young’s modulus for the polymer in the stress–strain graph shown below?
U
Materials for a purpose
Steel is used in large and small structures such as buildings and bridges because it is stiff and needs a large
stress to change its shape. Similarly, metals and ceramics are used in orthopaedic and dental prostheses
because of their strength, stiffness and bearing properties.
When producing a prostheses, it is important to select materials with similar mechanical properties to the body
part it is going to replace. These materials must also be biocompatible, non-toxic and not susceptible to decay or
changes in temperature. They must also be readily secured mechanically or chemically to hold them in place.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
Strain energy
Bungee cords are selected for their good energy-absorbing characteristics. Otherwise, a bungee jumper would
stop too quickly, which might cause injury. Similarly, our tendons, muscles and cartilage absorb large amounts of
energy to help avoid injury. The energy is absorbed during deformation caused by the forces doing work on that
part of the body. We use strain energy to describe the energy stored in a material when it is deformed.
Strain energy is equal to the work done to deform a material. In general, the strain energy per unit volume stored
in a material for any strain can be determined from the area under the stress–strain graph up to that particular
strain. The strain energy per unit volume is usually measured in joules per metre cubed. The unit J m–3 is
equivalent to N m–2, as:
= 1N m m 3
FS
1J m 3
O
= 1N m 2
PR
O
SAMPLE PROBLEM 16.6
The stress–strain characteristics of a particular material are shown below.
U
N
C
O
R
R
EC
TE
D
PA
G
E
a. Calculate how much energy per unit volume is needed to strain the material 0.2% (2 × 10–3).
b. The test specimen was 200 mm long and 12 mm in diameter. If the specimen fractured at a strain of 3 ×
10–3, estimate the energy required to fracture it.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
Solution:
a. The energy per unit volume found from the area under the curve up to a strain of 2 × 10–3:
1
 2  10 3  240  106 J m 3
2
 2.4  105 J m 3 .

b. Energy per unit volume found from the area under the curve up to a strain of 3 × 10–3:
1
1
 2  10 3  240  106  (240  280)  106  (3  10 3  2  10 3 ) J m 3
2
2
 (2.4  2.6)  105 J m 3

FS
 5.0  105 J m 3
O
Total energy to fracture (radius = 0.006 m; length = 0.200 m):
PR
O
 5.0  105    (0.006)2  0.200
 11.3J
G
E
The strain energy for the particular test piece, measured in joules, could also be found directly from the area
under the force–extension curve.
REVISION QUESTION 16.2
PA
If a material returns to its original shape when the force is removed, the energy that was stored is called elastic
strain energy.
U
N
C
O
R
R
EC
TE
D
A tendon with the stress–strain properties shown below has a cross-sectional area of 10–4 m2.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
a. How much energy per unit volume is needed to tear the tendon?
b. What is the total energy needed to tear the tendon?
c. What is the minimum force needed to tear the tendon?
Toughness
FS
We use the term toughness to describe the ability of a material to store energy up to the point of fracture. A
material with a greater strain energy up to fracture is said to be tougher than one requiring less energy.
Toughness can be determined from the total area under the tensile stress–strain curve for a material up to the
fracture strain.
R
R
EC
TE
D
PA
G
E
PR
O
O
SAMPLE PROBLEM 16.7
C
U
N
a. tougher
b. stronger
c. stiffer?
O
Consider the stress–strain graphs of the two materials, 1 and 2, in the figure above. Which material is:
Solution:
a. Material 2 is tougher because more energy per unit volume is needed to break it. This is evident from the
greater area under the stress–strain curve up to the fracture strain.
b. Material 1 is stronger. The height of the stress–strain curve shows that material 1 could tolerate a greater
stress than material 2.
c. Material 1 is stiffer, as shown by the steeper gradient of the stress–strain curve; it has a greater Young’s
modulus.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
Elastic behaviour
EC
TE
D
PA
G
E
PR
O
O
FS
A cyclist pulls on shorts to stretch them over the hips, but the deformation of the shorts is not permanent. When
the cyclist stops pulling, the shorts assume the shape of the body. If they did not, the shorts would fall down. This
is an example of reversible deformation that occurs in many materials, including metals used in structures like
bridges and buildings. When the force stops acting, the material returns to its original shape. Deformation that
disappears when the stress is removed is called elastic deformation.
R
R
The graph above shows the stress–strain behaviour of a test specimen. When the load was removed, the
specimen behaved elastically, recovering its original shape.
C
O
The maximum stress for which a material behaves elastically is called the elastic limit or yield stress. When
stretched beyond its elastic limit, a material will not return to its original shape.
N
Visco-elastic behaviour
U
Naturally occurring materials in our body — blood vessels, skin, tendons and bones — exhibit another type of
elasticity. The stress–strain graph of skin displayed previously shows that skin does not strain linearly when stress
is initially applied; the strain is time dependent. As the stress increases, the skin assumes linear elastic properties.
This time-dependent behaviour is largely attributed to the response of elastin fibres in the skin.
When a load is removed and the skin or other material returns to its original shape, the energy might not be
returned, which shows up as a loop on the stress–strain graph. The loop shown in the figure below is called a
hysteresis loop, which is a characteristic behaviour for tendons and skin. The unreturned energy is typically used
to do work within the system, and might be evident in the form of heat.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
TE
D
PA
For some materials loaded and unloaded within the elastic range, the energy absorbed during loading may not be
completely recovered. This is called hysteresis and the discrepancy appears as a hysteresis loop on a stress–
strain graph.
Plastic behaviour
U
N
C
O
R
R
EC
Deformation that does not completely recover when the force is removed is called plastic deformation. The panels
of a car, dented in an accident, have undergone plastic deformation. When you pull on a piece of chewing gum it
stretches, but the deformation is not reversible. We also plastically deform aluminium foil and cling wrap to the
shape of various containers. The plastic properties of materials are very useful for manufacturing and shaping
items, including some prosthetics. For example, wire is bent into shape for dental braces without breaking, and
polymers are used to form complex shapes when making a hand splint.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
TE
D
EC
O
R
R
The test specimen was loaded beyond its elastic limit, and then there was some elastic recovery, but the energy
used to stretch the specimen was not fully recovered.
C
Ductile
U
N
Materials that deform plastically before they fracture are said to be ductile. Most metals and polymers are ductile.
The steel tensile test piece shown in the figure below started as a uniform shape. As it was loaded, it elongated
and the cross-sectional area decreased. When unloaded, the test piece did not return to its original shape
because it had been loaded beyond its elastic limit; it had deformed plastically. Necking is the noticeable thinning
that occurs before fracture of many metals, and occurs where the material is weakest. After ductile fracture, the
broken pieces do not fit together well.
The percentage elongation of a material at fracture is often used as a measure of its ductility.
Brittle
Materials that are not ductile are called brittle. Brittle materials experience little or no plastic deformation before
fracture — less than about 5% strain. In general, the surface of a brittle failure is flat and the broken pieces could
be fitted back together to resemble the original item. The glass in figure below is an example of a brittle failure.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
EC
TE
D
PA
G
E
PR
O
O
FS
Note that the pieces can be put back together to look like the original object. Concrete, plaster and glass are
examples of brittle construction materials.
R
Although brittle materials are usually not as tough as ductile materials, the maximum stress to fracture may be
large. Consequently, brittle materials are sometimes strong.
R
Choosing materials to perform
N
C
O
Nature successfully uses materials with appropriate properties for a variety of purposes. For example, an eggshell
is strong enough to withstand the compressive stresses caused by the weight of brooding parents. However, a
hatching chick can easily break the shell. This is because the shell is brittle. Once the chick has pecked a hole in
the shell, cracks spread easily throughout the brittle material, causing it to break.
U
Similar to the shell of an egg, our skull must be strong in compression and be hard enough to resist penetration.
However, because it must resist larger forces, the skull needs to be both stronger and tougher with a larger elastic
limit than the brittle eggshell.
Our skin is not brittle; it is tough and strong in tension. These properties enable our skin to stretch over our bodies
while also providing protection from tearing.
For centuries, people used animal skins to cover timber-framed tents, and bridges were often built using wood or
stone. The materials used in tension are usually tough, such as tendons and the steel used for the cables
supporting a bridge like the West Gate Bridge. Concrete is not tough. It is a brittle material used in compression,
such as in footings and columns for bridges and buildings.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
While strength, stiffness and toughness are fundamental considerations in choosing a material for many
structures and machines, we must also consider other factors. For example, is the environment in which the
material will be used corrosive, hot, cold, wet or dry? How much does the material cost and is it readily available?
The Inuit used ice to build their igloos because it was readily available, strong enough to resist the resultant
compressive stresses and able to withstand the harsh Arctic environment. Bamboo is often used for scaffolding in
Asian countries. This is because it is readily available, cheap, light, easy to work with and strong.
FS
Engineers aim to build bridges and buildings so that they will behave in a ductile manner. Although the structures
are designed so that applied forces will not stress the materials beyond their elastic limit, choosing ductile
materials is a safeguard against large forces that could cause sudden and potentially catastrophic failures. Brittle
materials, which might be strong and readily used in compression, are seldom used in tension. The selection of a
material for structural use depends on mechanical properties like ductility and strength. However, we need to be
aware of factors that may alter the properties of the materials we use.
O
Materials for protheses
G
E
PR
O
When choosing materials to make a prosthesis, it is necessary to consider the stresses each component must
resist. Will each component be subject to an axial tensile or compressive stress? Bending or torsion? Does the
component move, rendering it susceptible to wear and tear from frictional forces? The properties of the available
materials also need to be determined according to their function. For example, the pylon in a below-knee
prosthetic must be strong in compression and able to resist some bending and torsion. It should also be stiff,
ductile and preferably with a weight similar to that of a natural leg. Consideration should also be given to how the
pylon can be made. Can it be readily cast or machined? In contrast, a cover over the pylon is most likely cosmetic
and other materials such as polyurethane foam and plastic might be appropriate because of their low weight and
the ease with which they form irregular shapes.
PA
Common construction materials
TE
D
The materials that we use for construction can be classified as coming from one of four groups — metals,
ceramics, polymers or composites; composite materials are composed of two or more different materials.
Strength and stiffness are two important properties necessary for structures, whether they are for a building or for
an artificial limb.
U
N
C
O
R
R
EC
Typical strength and stiffness values of these groups of materials are shown in the figure below.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
TE
D
The range of strength and stiffness for different materials
U
N
C
O
R
R
EC
Another useful way to display this information is by grouping the typical range of values of two properties of
materials together. This type of chart is often referred to as an Ashby chart.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
TE
D
EC
An Ashby chart showing strength and stiffness of different groups of materials
R
Materials with identical chemical composition do not always behave in the same way. Their behaviour might
depend on other factors such as ambient temperature, the duration and frequency of loading, and the
environment in which the material is used.
R
When the going gets hot
U
N
C
O
The properties of materials depend on temperature. For example, a decrease in temperature might cause a
ductile material to become brittle. At high temperatures, materials can deform plastically even when the stress is
less than the material’s elastic limit determined at room temperature.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
The mechanical properties of polymethyl methacrylate vary with temperature.
U
N
C
O
R
R
EC
TE
D
The temperature dependent behaviour of materials can be used as an advantage, as in the shaping of some
metals and plastics. A splint such as that shown in figure below was shaped to the profile of the person’s hand
while the thermoplastic was warm. As the thermoplastic cooled, it became stiffer and stronger.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
Tired out
Materials subjected to cyclic loads can fail at lower stresses than their yield strength. This failure is common in
metals and is called fatigue. For example, a paperclip can be broken by repeatedly bending and straightening it in
opposite directions. The maximum magnitude of the force you apply does not change, but the cyclic loading and
unloading causes cracks to spread and eventually fractures the clip. Similarly a tooth that is repeatedly subjected
to compressive stresses might eventually fracture.
FS
Cyclic loads are important to consider when selecting materials for joint replacements. When metal, a ductile
material, is used in an implant, it is more prone to fatigue than the biological material it replaces. In their early
years, metal-on-metal hip implants were known to last up to two years. The current generation of hip implants
involves other materials, and the hips can be reasonably expected to last more than ten years.
Given enough time
C
O
R
R
EC
TE
D
PA
G
E
PR
O
O
Creep is the time-dependent and permanent deformation of a material under a constant load. Both the
temperature and the size of the applied stress affect the rate at which creep occurs. The visco-elastic materials in
our body, particularly our skin, exhibit creep. The strain increases with time even when the stress is constant.
When stretched and kept at a constant deformation, the stress in our skin will decrease over time and it is said to
have relaxed.
U
N
Typical strain–time curve for a material showing creep under constant stress and temperature. Creep is evident in
most materials at higher temperatures; however, lead and some polymers will readily creep at room temperature.
Although some materials take years to show significant signs of creep, some soft metals and polymers show
signs of creep in a short time.
Metals
For centuries, people have used metals for a large variety of application. As shown in Ashby chart above, metals
are generally strong and stiff. They can be readily cast, machined, rolled, forged, drawn and extruded into
different shapes. Quenching and annealing are heat treatment techniques sometimes used to alter the hardness
and yield strength of metals without changing their chemical composition.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
Steel is frequently used in the construction of machines, bridges and buildings because it is economical, strong
and ductile. It is equally strong in tension and compression, and is a vital component in reinforced concrete.
Aluminium is also used in construction, particularly when weight is important, such as in aircraft frames. However,
aluminium is more expensive than steel to produce and fabricate.
There are many different types of steel, but they are all iron-based alloys. In general, increasing the percentage of
carbon in steel tends to make it stronger and less ductile, and adding manganese enhances its toughness. Steel
typically has a Young’s modulus of approximately 2 × 10–5 MPa.
EC
TE
D
PA
G
E
PR
O
O
FS
Steel responds instantaneously to stresses less than its yield stress, which for the steel used in construction is
typically 230–250 MPa. The transition from elastic to plastic behaviour in steel usually occurs suddenly at what is
called the upper yield point. When stressed beyond its upper yield point, steel deforms plastically. Eventually the
steel reaches its maximum stress, necks and fails. The stress–strain curve for an annealed steel is shown below.
R
Typical stress–strain curve for annealed steel
O
R
Metal in prosthetic limbs
U
N
C
Limb prostheses are functional replacements for a missing limb. Records show that steel and iron were used in
the manufacture of prosthetic arms as far back as the sixteenth century. Prior to that, wood and copper are known
to have been used for leg prostheses. The strength and stiffness of steel make it a good substitute for bone, but it
is significantly heavier for the user.
Stainless steel, aluminium and titanium are metals that are now used for manufacturing prosthetic limbs and
joints. These metals are readily available, although titanium is more expensive. Both stainless steel and titanium
can equal bone for strength and stiffness when acted on by axial forces as well as when bending or in torsion.
The ductility of these metals is an important consideration given the cyclic loading and unloading that occurs in
our body. However, the weight of metal prosthetics is larger than bone, and therefore they require more energy to
use, causing the user to tire sooner. For this reason, aluminium might be preferred over stainless steel and
titanium when considering large components such as the pylon in a leg prosthesis. The development of materials
such as carbon fibre and Kevlar, both strong and durable, has enabled lighter prostheses to be built.
In general, limb prostheses include a socket to join the prosthetic to the body, an attachment mechanism, and for
a dynamic prosthetic, a control mechanism. For a lower leg prosthesis like that shown in figure below, the pylon is
the main internal structure, preferably made from carbon fibre, titanium or aluminium. Metals are commonly used
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
TE
D
PA
G
E
PR
O
O
FS
when joining components, particularly if they are designed to move relative to each other. Some wood might be
used to structure the foot, but plastics and foams are suitable for the rest of the prosthesis.
An above-knee leg prosthesis
R
R
EC
Carbon fibre is an example of a composite — a material made by combining two or more different materials to
create a single material with enhanced performance characteristics, such as stiffness, strength and toughness.
Fibre reinforced composites (FRCs) such as carbon fibre have become competitive substitutes for traditional
materials, not just because of their weight, but also for the shapes that they can create. Fibre composites can also
exhibit good energy absorbing and storage properties.
O
AS A MATTER OF FACT
N
C
Could someone with lower leg prostheses have an advantage over athletes with natural legs?
U
This question was asked when Paralympic athlete Oscar Pistorius applied to compete at the 2012 London
Olympics. When running and responding to impact forces, the Pistorius’s prosthetic leg deformed, primarily about
the curve at the bottom, and absorbed the stress. In an athlete with a natural leg, the stress would also be
absorbed, but in the joints of their body: ankle, knee, hip and lower back. However, it was alleged that unlike an
athlete with natural legs, the carbon-fibre prostheses would rebound off the ground, returning a larger portion of
the stored energy, to the advantage of the runner. Is this possible?
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
TE
D
EC
R
R
O
N
Composites
C
AS A MATTER OF FACT
U
Both timber and bone are naturally occurring composites. Timber consists of hollow cellulose fibres bound
together in a matrix of lignin. Bone comprises a hard outer layer, cortical, which surrounds and protects a softer
inner region, trabecular.
Perhaps the earliest artificial composites developed for construction were mud bricks in which straw was mixed
with clay. The composite mix reduced cracking that occurred as the bricks dried and shrank. Reinforced concrete
is an artificial composite widely used for the past century in the construction industry.
Cellular reinforcement, such as honeycombs and foams, is used in the construction of aircraft and train carriages,
but most structural composites are a plastic matrix with fibre.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
Arm prostheses
Like our legs, our arms need to resist large forces when lifting objects or withstanding impacts. Our arms must do
this while also enabling the hands to perform delicate and complex tasks such as cleaning our teeth or playing a
musical instrument.
Prostheses that need to move about a joint might be operated by cables or even small motors to do the job that
muscles and tendons in a natural arm would perform. The splint in figure below is an example of a prosthesis that
assists in the rehabilitation of an injured hand. Note the use of external metal cables to transfer forces across the
joints of the hand and fingers. Traditionally, the body of the splint would be made from plaster. Now it is more
likely to be a thermoplastic or fibre reinforced composite such as fibreglass.
FS
Joint replacements
PR
O
O
Sometimes people need a replacement joint or other internal body part because of a congenital issue, injury,
disease such as osteoarthritis, or wear and tear from overuse or ageing. Stainless steel and titanium are used for
implants such as hip and knee replacements. These metals are also commonly used in dental work for braces
and implants. Stainless steel and titanium are generally biocompatible, hard and can be prepared so that they can
integrate into bone.
U
N
C
O
R
R
EC
TE
D
PA
G
E
There are different types of hip implants. However, as a ball and socket joint, they typically comprise a tapered
metal peg inserted into the head of the femur, to which is attached a ball to facilitate movement of the joint, and a
socket and cup fixed to the pelvis.
Metals are well suited for attachment to the femur because their mechanical properties are comparable to healthy
bone. Typically the femoral peg is stainless steel or titanium, and the other components are mostly made from
ceramics or hard polymers. The peg and cup might be mechanically fixed or cemented in place. These parts are
often coated with materials such as hydroxylapatite to facilitate the growth of bone and the eventual integration of
the replacement part with the existing bone.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
C
O
R
R
EC
TE
D
PA
G
E
PR
O
O
FS
As for all joint implants, the surgical insertion of a hip replacement comes with risks and complications. The risks
can include fracture of the femur, particularly if the bone is not healthy, and loosening of the peg or cup where
they are attached to the bone. As it is subject to frequent and heavy loads, the movement of the replacement hip
can also cause wear of the ball and socket. If debris created from wear and tear is not biocompatible, this can
cause complications. In Britain in 2010, blood poisoning was reported from certain metal-on-metal implants that
had worn and deposited potentially toxic metal into the bloodstream. Ceramic and polymer ball-and-socket joints
now provide an alternative wearing surface to earlier metal-on-metal implants. However, these materials also
create their own debris from wear and tear, which the body must deal with.
N
Materials in dentistry and stents
U
The advantages of the ductility of metals is also evident in their use in dental braces and in stents, which are
inserted into arteries. Shaped like a tube, stents are placed in diseased arteries to keep them open and to
facilitate blood flow. Usually made of metal mesh, a stent is implanted in the artery. A synthetic balloon already
within the stent is then inflated, deforming the stent to its intended size. The balloon is then removed to enable a
healthier blood flow.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
TE
D
EC
R
U
N
C
O
R
The malleability of metals is a useful behaviour that makes them tolerant to compressive forces. Softer metals
such as lead and gold can be easily pushed and hammered into shape. Dentists use materials that can be easily
shaped to fill cavities in teeth. Once in place, a filling must be resistant to biochemical attack from bodily fluids.
Gold has been used for more than a century for filling tooth cavities. It is malleable, but is now used less
frequently in part because of its cost. Amalgam (an alloy of mercury, silver, tin and copper) is a more costeffective mixture of metals, which forms a malleable putty at time of mixing . After shaping in situ by the dentist,
the amalgam sets and becomes a hard, strong and stiff filling for tooth cavities.
The properties of ceramics have also made them suitable for some dental work including caps. Ceramics are
typically hard, resistant to corrosion and can usually withstand high temperatures. Some ceramics are naturally
occurring and some are artificial substances.
There have been significant advances in the materials used in the manufacture of prostheses, particularly with the
development of composite materials for the structural components and electronic systems for controlling
movement. The human body is not built to last forever; however, will prostheses ever be as desirable as a natural
body part?
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
Chapter review
Summary
■
■
■
■
A force that pulls on something is called a tensile force.
A force that pushes on something is called a compressive force.
When a material is bent, part of it is in compression and part is in tension.
O
Deformation that is reversed when the load is removed is called elastic deformation.
FS
When a force is applied to a material, the material deforms. The amount of deformation depends on the size of
the force and the stiffness of the material.
Stress, σ, is the force per unit area of cross-section under load.
PR
O
Deformation that is not completely reversed when the load is removed is called plastic deformation.
Strain, ε, is the ratio of the change in length, ∆l, to the original length of the material under load, L.
When the stress–strain curve is a straight line, the gradient is called Young’s modulus, E. The relationship
between stress and strain is an expression of Hooke’s Law and is written in the form σ = E × ε. Young’s
modulus is a measure of the stiffness of a material.
G
E
■
Each part of a stationary structure must be in translational and rotational equilibrium.
The strain energy of a material is equal to the work done to deform it. The area under the stress–strain curve
measures the strain energy per unit volume of material.
Toughness is a measure of the energy required to fracture a material and is determined from the total area
under the stress–strain curve up to the fracture point.
PA
■
■
■
■
■
■
A structure is in equilibrium if the net force acting on it is zero and the net torque acting on it is zero.
Brittle materials show little or no plastic deformation before breaking.
TE
D
■
■
■
■
■
Ductile materials show plastic deformation before breaking.
Composite materials are made by combining two or more different materials to create a single material with
enhanced characteristics.
EC
Questions
R
Forces in the human body
U
N
C
O
R
1. The skull shown in figure below acts as a lever with its fulcrum at the top of the spine.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
a. Calculate the magnitude of the force in the muscles at the back of the neck.
TE
D
During a car crash, the shoulders of the person shown in the figure are restrained by a seatbelt. However,
their head is initially accelerated forward, to be resisted only by the muscles in the back of the neck.
b. On a diagram of a skull, show the forces that are now acting.
c. Calculate the force in the muscles at the back of the neck when the acceleration is 4g forward?
EC
d. What is the force in the spine when the acceleration is 4g forward?
U
N
C
O
R
R
2. Your jaw acts as a lever when you eat, hinging at the temporomandibular joint. If the force needed to bite a
carrot is 120 N, what force is required from the muscles shown in the figure below?
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
U
N
C
O
R
R
EC
TE
D
PA
3. When holding an arm horizontally and to the side as shown in figure, Ben’s arm acts as a lever that rotates at
the shoulder joint.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
PR
O
O
a. If the mass of Ben’s arm is 4 kg with its centre of mass at mid-length, what force is needed at B to keep his
arm horizontal?
The deltoid muscle group, which is the primary muscle group acting, inserts at the bone at approximately
16° to the horizontal.
b. What force must be provided by the deltoids?
G
E
c. When Ben also holds a 3 kg mass in his hand, what force must be provided by his deltoids?
U
N
C
O
R
R
EC
TE
D
PA
4. a. For the circus routine shown in the figure below, draw a diagram that shows the forces acting on the
performer.
b. The performer’s mass is 64 kg. Calculate the direction and magnitude of the force in each arm. (Assume
the vertical forces are equally distributed between each arm.)
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
Materials in the human body
5. At its mid-length, Belinda’s femur is approximately circular in cross-section with a diameter of 22 mm. If her
mass is 56 kg, calculate the stress in her femur.
6. a. What stress will cause a strain of 0.04 in a tendon with a Young’s modulus of 0.25 GPa?
b. If the original length of the tendon was 200 mm, how much has it stretched under this load?
7. A 2 mm diameter steel cable 5 m long lifts a 15 kN load. Assuming Young’s modulus for the steel is 200 GPa,
how much will the cable stretch?
8. A 12.7 mm square bar 50.8 mm in length is loaded in tension. The data shown in table 16.3 were collected.
FS
a. Convert the data to stress and strain.
b. Plot the data and calculate Young’s modulus.
O
c. What stress would cause a strain of 0.5% in a 10 mm square bar?
G
E
Length (mm)
50.80
50.90
50.95
51
51.05
51.10
PA
Force (kN)
0
72.4
108.6
144.8
161.2
189.5
PR
O
TABLE 16.3 Data for square bar
U
N
C
O
R
R
EC
TE
D
9. Estimate the stiffness of the material described in the graph shown below.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
TE
D
EC
R
R
O
C
U
N
10. The stress–strain characteristics for two different materials, A and B, tested to fracture are shown.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
a. Which material has the greater Young’s modulus?
PA
b. At the elastic limit, which material has the greater strain?
c. Which material is tougher?
d. Which material is more ductile?
TE
D
e. Which material is stronger?
11. What stress would create a strain of 0.0005 in a bone with a Young’s modulus of 18 GPa?
12. The results of a tensile test are given in table 16.4.
EC
a. Plot the stress–strain graph for this material.
b. Is the material brittle or ductile? Explain.
R
c. Calculate Young’s modulus for the material.
R
d. How much energy is stored in the material when it is stretched to twice its original length?
U
4
2
20
30
C
0
0
22
15
N
σ (MPa)
ε (%)
σ (MPa)
ε (%)
O
TABLE 16.4 Tensile test results
8
4
19
50
12
6
20
80
16
8
20
110
20
10
20
160
24
12
18
210
13. The stress–strain relationship for skin is shown in graph below.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
FS
O
PR
O
G
E
PA
a. Describe how the skin will behave when it is acted on by a force from zero to H.
U
N
C
O
R
R
EC
TE
D
The stress–strain relationship for another material, A, is shown below.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
b. If material A was used to make synthetic skin, what would happen as it was loaded from zero to a stress
H?
c. Would you consider this an adequate substitute for skin?
14. A 5 m long cable made from a linear elastic material stretches by 2 mm when a stress of 54 MPa is applied.
Determine the strain energy in the cable.
15. A 12.5 mm diameter aluminium bar was tested in tension. The bar fractured at a length of 55.13 mm. Table
16.5 shows the data collected up to the point of fracture.
a. Convert the data to stress versus strain.
b. Plot the stress–strain graph.
FS
c. On the graph, label:
i. elastic limit
O
ii. ultimate tensile strength
PR
O
iii. breaking strength.
d. Calculate:
i. elastic limit
ii. ultimate tensile strength
G
E
iii. breaking strength.
TE
D
R
EC
Length (mm)
50.00
50.02
50.07
50.13
50.18
50.75
52.00
53.00
54.00
55.13
R
Load (kN)
0
4.5
13.4
22.3
31.2
33.4
35.2
35.7
35.7
33.8
PA
TABLE 16.5 Data up to point of fracture
O
16. A dental technician is stretching a 40 mm long piece of stainless steel wire 1.2 mm in diameter. Stainless
steel has the following mechanical properties:
C
E = 195 GPa; Yield strength = 215 MPa; Tensile strength = 505 MPa.
N
a. What is the minimum force needed to deform the wire permanently?
U
b. How much must the wire be stretched to create a permanent change in length?
c. What is the maximum force that the wire can tolerate before it breaks?
17. The data sheet provided by a manufacturer for its fibre product stated that it had a Young’s modulus of 75 GPa
and an ultimate strength of 90 MPa. If the stress–strain curve for the fibre is linear, by how much would a 1 m
long fibre elongate before fracture?
18. A 0.500 m long piece of wire stretched 0.4 mm when a 6.0 kN force was applied. The wire had a diameter of
3.0 mm. Assuming that it was behaving in a linear elastic manner, what was:
a. the maximum stress
b. the maximum strain
c. the Young’s modulus
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
d. the strain energy
e. the total energy absorbed by the wire?
19. a. For each of the items listed below, which terms best describe the loads which they are most likely to
experience: tension, compression, bending or shear?
i.
strings of a tennis racquet
ii.
human skin
iii. blade of a kitchen knife
iv. human bone
a lift cable
FS
v.
vi. bicycle tube
O
vii. soft drink bottle
PR
O
viii. human tendon
ix. sole of a running shoe
x.
kitchen cling wrap
xi. silicon filler
G
E
b. Identify the relevant material properties for each; for example, elastic, plastic, stiff, brittle, ductile or tough.
U
N
C
O
R
R
EC
TE
D
PA
20. The dental implant shown in figure below comprises a titanium alloy replacement for the tooth root inserted
into the jaw. An abutment is then added to which a ceramic crown is fitted.
a. What are the properties of the titanium alloy and the ceramic tooth that make them suitable for this use in
the human body?
b. What factors might affect the success of this implant?
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd
21. To manufacture a 30 mm diameter pylon for a below-the-knee limb prostheses, three potential materials are
being examined. The mechanical properties of each material are shown in Table 16.6.
TABLE 16.6 Mechanical properties of material for protheses
Density (kg m–3)–3
Strength (MPa)
Young’s modulus (GPa)’
Bone
2000
200
20
Material A
4430
970
110
Material B
1400
190
30
Material C
2200
140
20
Material
U
N
C
O
R
R
EC
TE
D
PA
G
E
PR
O
O
FS
List and describe the advantages and disadvantages of each of the materials being considered relative to
natural bone.
Chapter 16 How do forces act on the human body?
© John Wiley & Sons Australia, Ltd