What Does An Option Price Mean?
... while when puts are held long, then forwards are also held long. The forwards trading strategy can be interpreted as a poor man’s delta-hedge of the initially OTM option. The terminology arises because the forward trading strategy is independent of both any estimate of volatility, either historical ...
... while when puts are held long, then forwards are also held long. The forwards trading strategy can be interpreted as a poor man’s delta-hedge of the initially OTM option. The terminology arises because the forward trading strategy is independent of both any estimate of volatility, either historical ...
Understanding the Relationship Between Total Revenue and
... When price changes, you can analyze the change in total revenue in terms of a price effect and a quantity effect. Elasticity determines which effect is greater after a change in price. Begin this section by reviewing the formula for total revenue: TR = P x Q. The box on the left summarizes the relat ...
... When price changes, you can analyze the change in total revenue in terms of a price effect and a quantity effect. Elasticity determines which effect is greater after a change in price. Begin this section by reviewing the formula for total revenue: TR = P x Q. The box on the left summarizes the relat ...
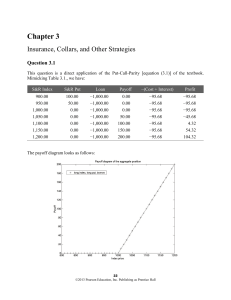
Chapter 3
... The strategy of buying a call (or put) and selling a call (or put) at a higher strike is called call (put) bull spread. In order to draw the profit diagrams, we need to find the future value of the cost of entering in the bull spread positions. We have: Cost of call bull spread: ($120.405 − $93.809) ...
... The strategy of buying a call (or put) and selling a call (or put) at a higher strike is called call (put) bull spread. In order to draw the profit diagrams, we need to find the future value of the cost of entering in the bull spread positions. We have: Cost of call bull spread: ($120.405 − $93.809) ...
Fair Value of Life Liabilities with Embedded Options: an Application
... if the regression involves all paths, more than two or three times as many functions may be needed to obtain the same level of accuracy as obtained by the estimator based on in-the-money paths. This is our case, since the intrinsic value is not, for example, the standard payoff of a put, but is give ...
... if the regression involves all paths, more than two or three times as many functions may be needed to obtain the same level of accuracy as obtained by the estimator based on in-the-money paths. This is our case, since the intrinsic value is not, for example, the standard payoff of a put, but is give ...
chapter overview
... chapter, and interest rate risk, which is the subject of this chapter. Before studying the various potential sources of interest rate risk and the instruments that are designed to hedge against these risks, the chapter begins with a presentation of the concept of discounted present value and how it ...
... chapter, and interest rate risk, which is the subject of this chapter. Before studying the various potential sources of interest rate risk and the instruments that are designed to hedge against these risks, the chapter begins with a presentation of the concept of discounted present value and how it ...
The Greek Letters
... Theta (Q) of a derivative (or portfolio of derivatives) is the rate of change of the value with respect to the passage of time The theta of a call or put is usually negative. This means that, if time passes with the price of the underlying asset and its volatility remaining the same, the value of a ...
... Theta (Q) of a derivative (or portfolio of derivatives) is the rate of change of the value with respect to the passage of time The theta of a call or put is usually negative. This means that, if time passes with the price of the underlying asset and its volatility remaining the same, the value of a ...
Options-Implied Probability Density Functions for Real Interest Rates
... same methodology to obtain the annualized implied volatility of options on ten-year nominal Treasury futures—a long-standing and very liquid options market. These are shown in Figure 2. The options-implied volatility of a ten-year nominal futures contract was also elevated in early 2009, but not as ...
... same methodology to obtain the annualized implied volatility of options on ten-year nominal Treasury futures—a long-standing and very liquid options market. These are shown in Figure 2. The options-implied volatility of a ten-year nominal futures contract was also elevated in early 2009, but not as ...
Optimal Delta Hedging for Options
... A number of researchers have implemented stochastic volatility models and used the models’ assumptions to convert the usual delta to an MV delta. They have found that this produces an improvement in delta hedging performance, particularly for out-of-the-money options. The researchers include Bakshi ...
... A number of researchers have implemented stochastic volatility models and used the models’ assumptions to convert the usual delta to an MV delta. They have found that this produces an improvement in delta hedging performance, particularly for out-of-the-money options. The researchers include Bakshi ...
Option pricing with discrete dividends
... Arbitrage example: In the case of European options, the above techniques are ad hoc, but get the job done (in most cases) when the corrections are properly carried out. To give you an idea of when it really goes wrong, consider the model of choice for American call options on stocks whose cum divide ...
... Arbitrage example: In the case of European options, the above techniques are ad hoc, but get the job done (in most cases) when the corrections are properly carried out. To give you an idea of when it really goes wrong, consider the model of choice for American call options on stocks whose cum divide ...
Oregon State University
... intermediate Treasury Bond asset class is captured in the following premiums: a) Inflation premium b) Maturity premium c) Inflation and maturity premiums d) Inflation, maturity and tax premiums e) Inflation, maturity and illiquidity premiums 9. The table below provides returns on a portfolio along w ...
... intermediate Treasury Bond asset class is captured in the following premiums: a) Inflation premium b) Maturity premium c) Inflation and maturity premiums d) Inflation, maturity and tax premiums e) Inflation, maturity and illiquidity premiums 9. The table below provides returns on a portfolio along w ...
Pricing with Splines - Annals of Economics and Statistics
... The standard for option pricing is the Black-Scholes approach (BLACK, SCHOLES [1973]), which assumes i.i.d. Gaussian geometric stock returns, continuous trading and derives an analytical formula for pricing European calls from the arbitrage free restrictions. The derivative prices and the associated ...
... The standard for option pricing is the Black-Scholes approach (BLACK, SCHOLES [1973]), which assumes i.i.d. Gaussian geometric stock returns, continuous trading and derives an analytical formula for pricing European calls from the arbitrage free restrictions. The derivative prices and the associated ...
Unconstrained Fitting of Non-Central Risk-Neutral
... Numerical Results Description of the Numerical Tests ...
... Numerical Results Description of the Numerical Tests ...
Derivatives Market in inDia: a success story
... contracts can be either standardised or customised. There are two types of options: ‘call’ and ‘put’ options. Call options contracts give the purchaser the right to buy a specified quantity of a commodity or financial asset at a particular price (the exercise price) on or before a certain future dat ...
... contracts can be either standardised or customised. There are two types of options: ‘call’ and ‘put’ options. Call options contracts give the purchaser the right to buy a specified quantity of a commodity or financial asset at a particular price (the exercise price) on or before a certain future dat ...
Option Hedging with Smooth Market Impact
... Guéant and Pu [2015] have solved a model very similar to ours, including both temporary and permanent price impact. They use a utility function rather than our meanvariance optimization. They distinguish between cash settlement and physical delivery, whereas our intraday model assumes the position w ...
... Guéant and Pu [2015] have solved a model very similar to ours, including both temporary and permanent price impact. They use a utility function rather than our meanvariance optimization. They distinguish between cash settlement and physical delivery, whereas our intraday model assumes the position w ...
DETERMINANTS OF IMPLIED VOLATILITY FUNCTION ON THE
... direction. This indicates the expensiveness of option premium for the traders. We compute IV (σit) by solving the Black-Scholes (1973) formula for each observed European call (Cit) and put (Pit) option closing price as shown in Equations (1) and (2): Cit = S0 (N d1) – Ke-rT N(d2) ...
... direction. This indicates the expensiveness of option premium for the traders. We compute IV (σit) by solving the Black-Scholes (1973) formula for each observed European call (Cit) and put (Pit) option closing price as shown in Equations (1) and (2): Cit = S0 (N d1) – Ke-rT N(d2) ...