High School – Geometry
... Use coordinates to prove simple geometric theorems algebraically G-GPE.4. Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies ...
... Use coordinates to prove simple geometric theorems algebraically G-GPE.4. Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies ...
Newsletter – Ch 2
... two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them. 8.G.3: Describe the effect of dilations, translations, ro ...
... two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them. 8.G.3: Describe the effect of dilations, translations, ro ...
Honors Geometry
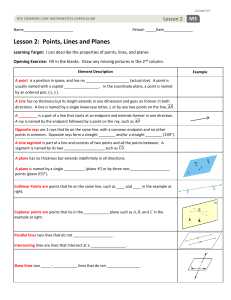
... Complete with Always, Sometimes, or Never 1. __________ Two <’s that are supplementary ___________form a linear pair. 2. __________ Two <’s that form a linear pair are ____supplementary. 3. __________Two congruent angles are _________right. 4. __________Two right angles are ___________congruent. 5. ...
... Complete with Always, Sometimes, or Never 1. __________ Two <’s that are supplementary ___________form a linear pair. 2. __________ Two <’s that form a linear pair are ____supplementary. 3. __________Two congruent angles are _________right. 4. __________Two right angles are ___________congruent. 5. ...
Ch. 3 Review Answers
... For numbers 11 – 13, write an equation in slope-intercept form for the line that satisfies the given condition. 11. Passes through (–7, –4), parallel to y ...
... For numbers 11 – 13, write an equation in slope-intercept form for the line that satisfies the given condition. 11. Passes through (–7, –4), parallel to y ...
2015-2016 Geometry 2nd Quarter Mathematics Scope and Sequence
... transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints. Use coordinates to prove simple geometric theorems algebraically. For e ...
... transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints. Use coordinates to prove simple geometric theorems algebraically. For e ...
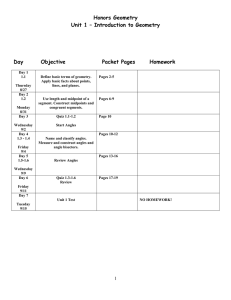
Ch 1 Notes
... Section 1.7: Find Perimeter, Circumference, and Area Standards: 8.0 Students know, derive, and solve problems involving the perimeter, circumference, area, volume, lateral area, and surface area of common geometric figures. 10.0 Students compute areas of polygons, including rectangles, scalene tria ...
... Section 1.7: Find Perimeter, Circumference, and Area Standards: 8.0 Students know, derive, and solve problems involving the perimeter, circumference, area, volume, lateral area, and surface area of common geometric figures. 10.0 Students compute areas of polygons, including rectangles, scalene tria ...
GEOMETRY – MIDDLE SCHOOL Link to: Geometry Curriculum
... b) verify the parallelism, using algebraic and coordinate methods as well as deductive proofs; and c) solve real-world problems involving angles formed when parallel lines are cut by a transversal. The student will use pictorial representations, including computer software, constructions, and coordi ...
... b) verify the parallelism, using algebraic and coordinate methods as well as deductive proofs; and c) solve real-world problems involving angles formed when parallel lines are cut by a transversal. The student will use pictorial representations, including computer software, constructions, and coordi ...
Lesson Plan Template - Trousdale County Schools
... paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. ...
... paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. ...
Extra Practice Problems for the Final Exam
... 26. Two American flags of different dimensions are properly folded into two similar isosceles right triangles. The ratio of the length of the legs of the smaller triangle to that of the larger triangle is 4 : 5. If the length of the hypotenuse of the larger triangle is 2 feet, what is the length of ...
... 26. Two American flags of different dimensions are properly folded into two similar isosceles right triangles. The ratio of the length of the legs of the smaller triangle to that of the larger triangle is 4 : 5. If the length of the hypotenuse of the larger triangle is 2 feet, what is the length of ...
Cartesian coordinate system
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, n Cartesian coordinates (an element of real n-space) specify the point in an n-dimensional Euclidean space for any dimension n. These coordinates are equal, up to sign, to distances from the point to n mutually perpendicular hyperplanes.The invention of Cartesian coordinates in the 17th century by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra. Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by Cartesian equations: algebraic equations involving the coordinates of the points lying on the shape. For example, a circle of radius 2 in a plane may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 4.Cartesian coordinates are the foundation of analytic geometry, and provide enlightening geometric interpretations for many other branches of mathematics, such as linear algebra, complex analysis, differential geometry, multivariate calculus, group theory and more. A familiar example is the concept of the graph of a function. Cartesian coordinates are also essential tools for most applied disciplines that deal with geometry, including astronomy, physics, engineering and many more. They are the most common coordinate system used in computer graphics, computer-aided geometric design and other geometry-related data processing.