Wojcik, K
... Step 1: Create (fold) a line m that passes through the bottom right corner of your sheet of paper. Let be the given angle. Step 2: Create the lines l1 and l2 parallel to the bottom edge lb such that l1 is equidistant to l2 and lb. Step 3: Let P be the lower left vertex and let Q be the intersection ...
... Step 1: Create (fold) a line m that passes through the bottom right corner of your sheet of paper. Let be the given angle. Step 2: Create the lines l1 and l2 parallel to the bottom edge lb such that l1 is equidistant to l2 and lb. Step 3: Let P be the lower left vertex and let Q be the intersection ...
KUTA Software Geometry
... Go to the KUTASoftware website to find the topics below, or press “control” while clicking on the topic from this page. ...
... Go to the KUTASoftware website to find the topics below, or press “control” while clicking on the topic from this page. ...
Lesson Plan - University of Cincinnati
... For the most part, I was pleased with the lesson. The amount of content was pretty good – a few students finished and were able to do extra credit work. Some didn’t finish. But at least they were all engaged in it and seemed to enjoy the work, The students were mostly enthusiastic. A few seemed over ...
... For the most part, I was pleased with the lesson. The amount of content was pretty good – a few students finished and were able to do extra credit work. Some didn’t finish. But at least they were all engaged in it and seemed to enjoy the work, The students were mostly enthusiastic. A few seemed over ...
Dilations Answer Key
... 2. Drag the Scale factor slider. JK is the dilated image of AB (the preimage). The ratio of the length of JK to the length of AB is the scale factor. A. What happens to JK when the scale factor is greater than 1? It is longer than AB . B. What happens to JK when the scale factor is less than 1? It i ...
... 2. Drag the Scale factor slider. JK is the dilated image of AB (the preimage). The ratio of the length of JK to the length of AB is the scale factor. A. What happens to JK when the scale factor is greater than 1? It is longer than AB . B. What happens to JK when the scale factor is less than 1? It i ...
Fetac Mathematics Level 4 Code 4N1987 Geometry Name : Date:
... Description of contents. 2.1 Describe simple geometric shapes associated with the home and workplace 2.2 Recognize folding symmetry and rotational symmetry in common shapes 2.3 Plot graphs of ordered pairs in the coordinate plane showing the relationship between two variables, using real life situat ...
... Description of contents. 2.1 Describe simple geometric shapes associated with the home and workplace 2.2 Recognize folding symmetry and rotational symmetry in common shapes 2.3 Plot graphs of ordered pairs in the coordinate plane showing the relationship between two variables, using real life situat ...
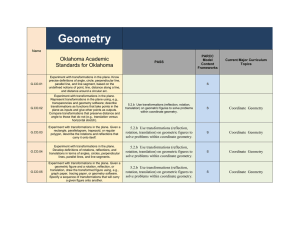
Geometry Common Core Standards and Sequence List Grade
... and coefficients. B. Interpret complicated expressions by viewing one or more of their parts as a single entity. For example, interpret P(1+r)n as the product of P and a factor not depending on P. Order of ...
... and coefficients. B. Interpret complicated expressions by viewing one or more of their parts as a single entity. For example, interpret P(1+r)n as the product of P and a factor not depending on P. Order of ...
Geometry Grade Level: 9 (with Recommendation), 10, 11, 12 Length
... 7. Use coordinates to compute perimeters of polygons and areas of triangles and rectangles, e.g., using the distance formula.★ Geometric Measurement and Dimension G-GMD Explain volume formulas and use them to solve problems. 1. Give an informal argument for the formulas for the circumference of a ci ...
... 7. Use coordinates to compute perimeters of polygons and areas of triangles and rectangles, e.g., using the distance formula.★ Geometric Measurement and Dimension G-GMD Explain volume formulas and use them to solve problems. 1. Give an informal argument for the formulas for the circumference of a ci ...
Geometry - BAschools.org
... algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point (0, 2). ...
... algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point (0, 2). ...
Cartesian coordinate system
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, n Cartesian coordinates (an element of real n-space) specify the point in an n-dimensional Euclidean space for any dimension n. These coordinates are equal, up to sign, to distances from the point to n mutually perpendicular hyperplanes.The invention of Cartesian coordinates in the 17th century by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra. Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by Cartesian equations: algebraic equations involving the coordinates of the points lying on the shape. For example, a circle of radius 2 in a plane may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 4.Cartesian coordinates are the foundation of analytic geometry, and provide enlightening geometric interpretations for many other branches of mathematics, such as linear algebra, complex analysis, differential geometry, multivariate calculus, group theory and more. A familiar example is the concept of the graph of a function. Cartesian coordinates are also essential tools for most applied disciplines that deal with geometry, including astronomy, physics, engineering and many more. They are the most common coordinate system used in computer graphics, computer-aided geometric design and other geometry-related data processing.