Distance, Ruler Postulate and Plane Separation Postulate
... ● Note that we've now gone from Euclid's straight-edge to a ruler with numerical measuring marks on it ● The ruler is a function that gives a one to one correspondence between points on lines and real numbers ● The ruler function must identify every segment with a distance ● A function with the corr ...
... ● Note that we've now gone from Euclid's straight-edge to a ruler with numerical measuring marks on it ● The ruler is a function that gives a one to one correspondence between points on lines and real numbers ● The ruler function must identify every segment with a distance ● A function with the corr ...
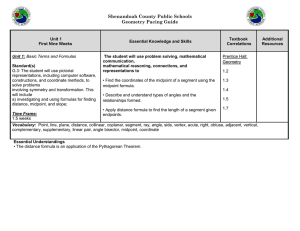
Geometry Pacing Guide
... Vocabulary: Parallel, skew, interior, exterior, corresponding, perpendicular, alternate, slope Essential Understandings • Parallel lines intersected by a transversal form angles with specific relationships. • Some angle relationships may be used when proving that two lines intersected by a transvers ...
... Vocabulary: Parallel, skew, interior, exterior, corresponding, perpendicular, alternate, slope Essential Understandings • Parallel lines intersected by a transversal form angles with specific relationships. • Some angle relationships may be used when proving that two lines intersected by a transvers ...
8-5: Butterflies, Pinwheels, and Wallpaper
... 1c. counterclockwise rotation of 90° about the origin 1d. counterclockwise rotation of 180° about the origin 1e. translation that “moves” points a units horizontally and b units vertically ...
... 1c. counterclockwise rotation of 90° about the origin 1d. counterclockwise rotation of 180° about the origin 1e. translation that “moves” points a units horizontally and b units vertically ...
\ Plainfield Public Schools Mathematics Rigorous Curriculum Design
... measurement have on triangles? . How do shapes change after each transformation? How are they the same? How do you manipulate a figure on the coordinate plane? What are some examples from the real world of transformational geometry? Given the pre-image, how can you determine what transformation has ...
... measurement have on triangles? . How do shapes change after each transformation? How are they the same? How do you manipulate a figure on the coordinate plane? What are some examples from the real world of transformational geometry? Given the pre-image, how can you determine what transformation has ...
ExamView - SLO #2 POST TEST.tst
... based on the undefined notions of point, line, distance along a line, and distance around a circular arc. 7. C ...
... based on the undefined notions of point, line, distance along a line, and distance around a circular arc. 7. C ...
Geometry 3rd Nine Weeks Pacing Guide Summary
... 14. [G-SRT.1] Verify experimentally the properties of dilations given by a center and a scale factor. ~A dilation takes a line not passing through the center of the dilation to a parallel line and leaves a line passing through the center unchanged. ~The dilation of a line segment is longer or shorte ...
... 14. [G-SRT.1] Verify experimentally the properties of dilations given by a center and a scale factor. ~A dilation takes a line not passing through the center of the dilation to a parallel line and leaves a line passing through the center unchanged. ~The dilation of a line segment is longer or shorte ...
Module 5 Revision Check
... ◊ Generate sequences for square and triangular numbers, powers of 2 and 10 ◊ Find the nth term of a sequence ...
... ◊ Generate sequences for square and triangular numbers, powers of 2 and 10 ◊ Find the nth term of a sequence ...
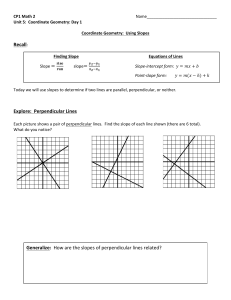
Cartesian coordinate system
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, n Cartesian coordinates (an element of real n-space) specify the point in an n-dimensional Euclidean space for any dimension n. These coordinates are equal, up to sign, to distances from the point to n mutually perpendicular hyperplanes.The invention of Cartesian coordinates in the 17th century by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra. Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by Cartesian equations: algebraic equations involving the coordinates of the points lying on the shape. For example, a circle of radius 2 in a plane may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 4.Cartesian coordinates are the foundation of analytic geometry, and provide enlightening geometric interpretations for many other branches of mathematics, such as linear algebra, complex analysis, differential geometry, multivariate calculus, group theory and more. A familiar example is the concept of the graph of a function. Cartesian coordinates are also essential tools for most applied disciplines that deal with geometry, including astronomy, physics, engineering and many more. They are the most common coordinate system used in computer graphics, computer-aided geometric design and other geometry-related data processing.