Trigonometric Ratios of Any Angle
... If the rotation is counterclockwise, the angle has positive measure. If the rotation is clockwise, the angle has negative measure. The rotation is usually indicated by a directed arrow starting from the positive X-axis. For a rotation angle, the acute angle built to the X-axis is called a reference ...
... If the rotation is counterclockwise, the angle has positive measure. If the rotation is clockwise, the angle has negative measure. The rotation is usually indicated by a directed arrow starting from the positive X-axis. For a rotation angle, the acute angle built to the X-axis is called a reference ...
5.6 UNITARY AND ORTHOGONAL MATRICES
... The purpose of this section is to examine square matrices whose columns (or rows) are orthonormal. The standard inner product and the euclidean 2-norm are the only ones used in this section, so distinguishing subscripts are omitted. ...
... The purpose of this section is to examine square matrices whose columns (or rows) are orthonormal. The standard inner product and the euclidean 2-norm are the only ones used in this section, so distinguishing subscripts are omitted. ...
Examples 2.3 - IHMC Public Cmaps (3)
... DESSERT Jessica does a survey on the cost of four different desserts at three local restaurants. At restaurant A, a slice of apple pie is priced at $2.25, a brownie sundae is priced at $2.95, a slice of apple cobbler is priced at $1.95, and an ice cream cone is priced at $1.10. At restaurant B, appl ...
... DESSERT Jessica does a survey on the cost of four different desserts at three local restaurants. At restaurant A, a slice of apple pie is priced at $2.25, a brownie sundae is priced at $2.95, a slice of apple cobbler is priced at $1.95, and an ice cream cone is priced at $1.10. At restaurant B, appl ...
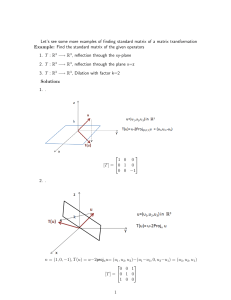
Find the standard matrix of the gi
... To be able to define inverse of a matrix transformation we need to have one-to-one matrix operator Definition: A matrix transformation T : Rn → Rm is said to be one-to-one if T maps distinct vectors (points) in Rn into distinct vectors (points) in Rm . That is for each w in the range of T, there is ...
... To be able to define inverse of a matrix transformation we need to have one-to-one matrix operator Definition: A matrix transformation T : Rn → Rm is said to be one-to-one if T maps distinct vectors (points) in Rn into distinct vectors (points) in Rm . That is for each w in the range of T, there is ...