Shape Matching under Rigid Motion
... If Q is convex, the running time for the translation case can be improved to O(n log n + ε−3 log2.5 n log logε n ). When both P and Q are general polygonal shapes, we can switch the roles of P and Q, so the error bound ε · area(P ) is equivalent to ε · min{area(P ), area(Q)}. In comparison with the ...
... If Q is convex, the running time for the translation case can be improved to O(n log n + ε−3 log2.5 n log logε n ). When both P and Q are general polygonal shapes, we can switch the roles of P and Q, so the error bound ε · area(P ) is equivalent to ε · min{area(P ), area(Q)}. In comparison with the ...
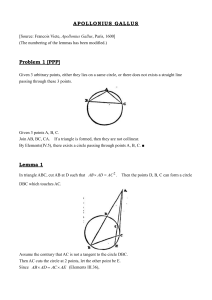
Appendix 1
... • We make no reference to results such as Pasch’s property and the “crossbar theorem”. (That is, we do not expect students to consider the necessity to prove such results or to have them given as axioms.) • We refer to “the number of degrees” in an angle, whereas Barry treats this more correctly as ...
... • We make no reference to results such as Pasch’s property and the “crossbar theorem”. (That is, we do not expect students to consider the necessity to prove such results or to have them given as axioms.) • We refer to “the number of degrees” in an angle, whereas Barry treats this more correctly as ...