114
... Calculations were carried out at the MC-SCF level of theory, with standard minimal (STO-3G)'6a and split-valence shell (4-3 1G)16bbasis sets. The MC-SCF and CI codes'' are used in conjunction with the GAUSSIAN82 series of programs." The valence space used in the present MC-SCF computations consists ...
... Calculations were carried out at the MC-SCF level of theory, with standard minimal (STO-3G)'6a and split-valence shell (4-3 1G)16bbasis sets. The MC-SCF and CI codes'' are used in conjunction with the GAUSSIAN82 series of programs." The valence space used in the present MC-SCF computations consists ...
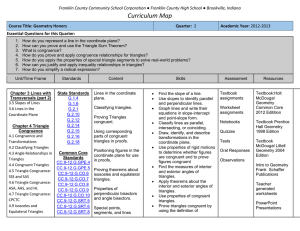
Geom_Unit2_Plan - Connecticut Core Standards
... Isosceles Triangle Theorem: If two sides of a triangle are congruent, then the angles opposite these sides are congruent. Isosceles Triangle Converse: If two angles of a triangle are congruent, then the sides opposite these angles are congruent. Equilateral Triangle Theorem: If all three sides of a ...
... Isosceles Triangle Theorem: If two sides of a triangle are congruent, then the angles opposite these sides are congruent. Isosceles Triangle Converse: If two angles of a triangle are congruent, then the sides opposite these angles are congruent. Equilateral Triangle Theorem: If all three sides of a ...
Equivalents to the Euclidean Parallel Postulate In this section we
... if two lines are cut by a transversal such that the interior angles on one side of the transversal are supplementary, the lines are parallel. Thus n and m are parallel, and by EPP n is the only line through P that is parallel to m. Thus l is not parallel to m, and must meet. They must meet on the si ...
... if two lines are cut by a transversal such that the interior angles on one side of the transversal are supplementary, the lines are parallel. Thus n and m are parallel, and by EPP n is the only line through P that is parallel to m. Thus l is not parallel to m, and must meet. They must meet on the si ...