Unit 8 Plane Geometry
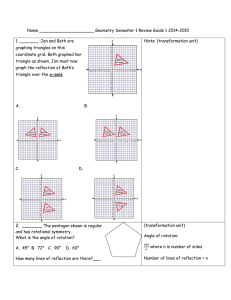
... midpoints of the three sides. 2- Join the midpoints of the sides. 3- Determine the area of the small triangle in the middle formed by joining the midpoints. 4- Determine the area of the large triangle. 5- Use the Calculator to divide the area of the large triangle by the area of the smaller triangle ...
... midpoints of the three sides. 2- Join the midpoints of the sides. 3- Determine the area of the small triangle in the middle formed by joining the midpoints. 4- Determine the area of the large triangle. 5- Use the Calculator to divide the area of the large triangle by the area of the smaller triangle ...