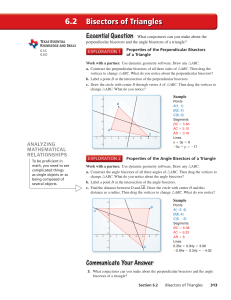
On Lobachevsky`s trigonometric formulae
... the family of non-intersecting lines was used by the three founders of hyperbolic geometry. 14In using the transitivity property, it is necessary to keep track of the direction of parallelism for pairs of parallel lines involved. ...
... the family of non-intersecting lines was used by the three founders of hyperbolic geometry. 14In using the transitivity property, it is necessary to keep track of the direction of parallelism for pairs of parallel lines involved. ...
Math 2 Name Lesson 4-3: Proving Triangle Similarity, Part 1 I can
... Corresponding Angles: Two angles that lie on the same side of a transversal, in corresponding positions with respect to the two lines that the transversal intersects. If the transversal intersect parallel lines, corresponding angles are congruent. Angles _____ and ______ in the above figure are an e ...
... Corresponding Angles: Two angles that lie on the same side of a transversal, in corresponding positions with respect to the two lines that the transversal intersects. If the transversal intersect parallel lines, corresponding angles are congruent. Angles _____ and ______ in the above figure are an e ...
Minimal tangent visibility graphs
... clear that a pseudo-triangulation always exists and that the bitangents of the boundary of the convex hull of the obstacles are edges of any pseudo-triangulation. A pseudo-triangulation of a collection of six obstacles is depicted in Fig. 3. L e m m a 2.1. The bounded free faces of any pseudo-triang ...
... clear that a pseudo-triangulation always exists and that the bitangents of the boundary of the convex hull of the obstacles are edges of any pseudo-triangulation. A pseudo-triangulation of a collection of six obstacles is depicted in Fig. 3. L e m m a 2.1. The bounded free faces of any pseudo-triang ...